
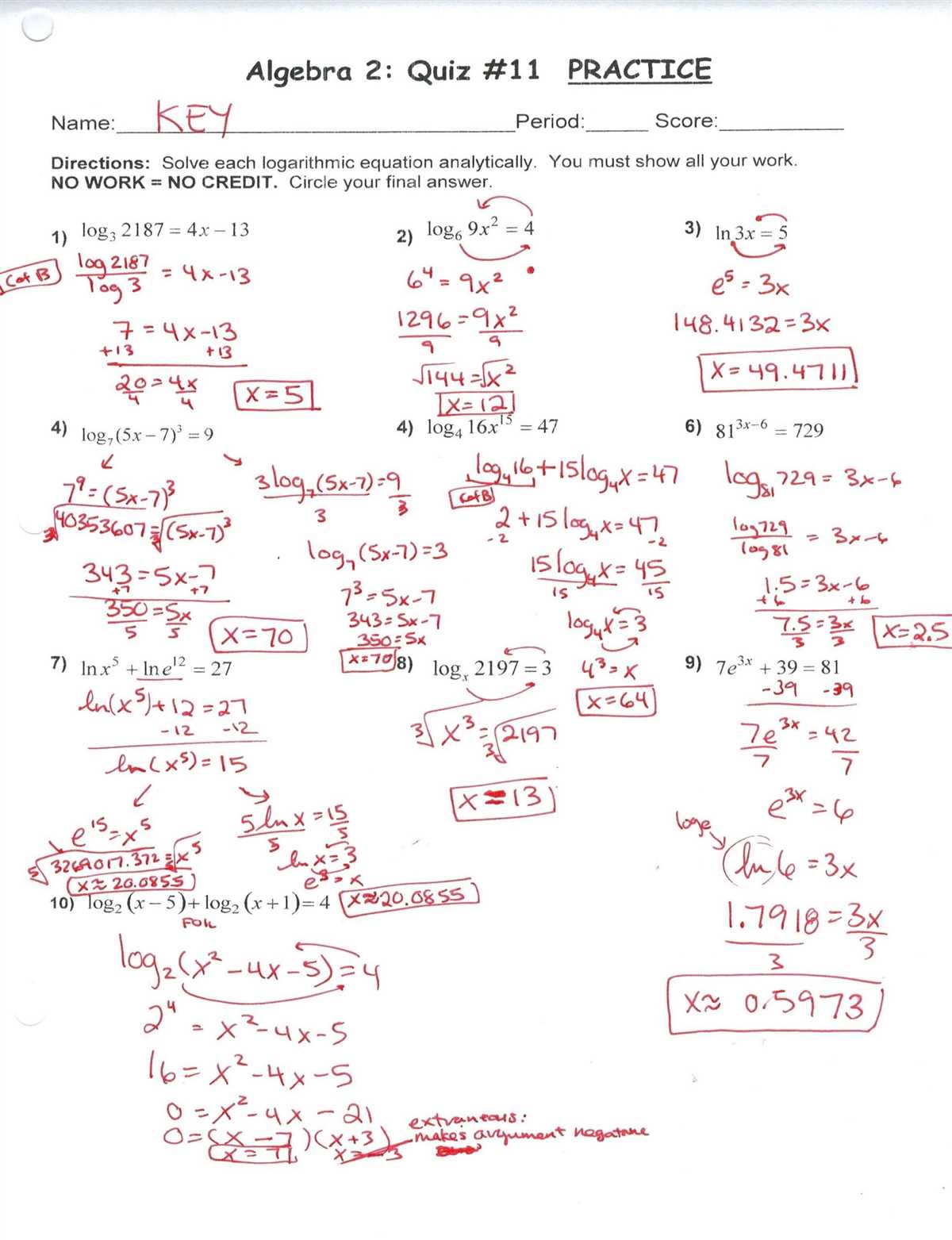
Absolute value inequalities are a key topic in algebra, and they often appear in word problems that involve real-world scenarios. Working through these types of problems can help students develop their problem-solving skills and deepen their understanding of algebraic concepts.
Absolute value inequalities can be challenging for students because they involve understanding the relationship between absolute values and inequalities. These problems require students to consider both the positive and negative solutions to an equation and determine which values satisfy the given inequality.
To help students practice solving absolute value inequalities and apply them to real-life situations, worksheets are a valuable resource. These worksheets provide students with a variety of word problems that require them to translate the given information into inequality equations and determine the range of possible solutions.
This Absolute Value Inequalities Word Problems Worksheet with Answers PDF includes a range of problems, from simple to complex, allowing students to gradually build their skills. The provided answers can be used for self-assessment or to check their work, ensuring that students are on the right track and enabling them to learn from their mistakes.
Absolute Value Inequalities Word Problems Worksheet with Answers PDF

Absolute value inequalities are mathematical expressions that include absolute value signs and inequalities. These types of inequalities can be represented on a coordinate plane and can be solved using various methods. To practice solving absolute value inequalities, students often complete worksheets with word problems that require them to interpret and solve real-life scenarios involving absolute value inequalities. These worksheets typically have a variety of problems that test students’ understanding of the concept.
One example of a word problem that could be included in an absolute value inequalities worksheet is as follows: “A store is having a sale where all items are discounted by at least 20%. If the original price of a dress is $80, what is the range of possible sale prices?” To solve this problem, students would first set up an absolute value inequality using the discount percentage and the original price. They would then solve the inequality to find the range of possible sale prices.
An absolute value inequalities word problems worksheet with answers in PDF format provides a convenient way for students to practice solving these types of problems. The PDF format allows for easy printing and sharing of the worksheet, making it accessible for use in a classroom setting or for individual practice at home. The answers included in the PDF file provide immediate feedback for students, allowing them to check their work and learn from any mistakes they may have made.
Overall, an absolute value inequalities word problems worksheet with answers in PDF format is a valuable resource for students learning about and practicing solving absolute value inequalities. It provides them with the opportunity to apply their knowledge to real-life situations, improve their problem-solving skills, and receive immediate feedback on their work.
What Are Absolute Value Inequalities?

Absolute value inequalities are a type of mathematical expression that involves the absolute value function and a comparison operator, such as less than (<), greater than (>), less than or equal to (≤), or greater than or equal to (≥). The absolute value function is denoted by two vertical bars surrounding the expression within them.
These inequalities represent a range of possible values for a variable that satisfy the given conditions. The absolute value function is used to determine the distance between a number and zero on a number line, regardless of its sign. Therefore, absolute value inequalities involve finding the values of the variable that are within a certain distance from the origin or a specific reference point.
To solve absolute value inequalities, one must consider two cases: when the expression inside the absolute value is positive and when it is negative. In each case, the absolute value can be removed by applying the appropriate inequality. The final solution is the combination of the solutions from both cases.
These types of inequalities often arise in real-world scenarios, such as when dealing with distances, temperatures, or any situation where the magnitude of a quantity is more important than its specific value. Solving absolute value inequalities allows us to determine the range of values that satisfy the given conditions and make informed decisions in various contexts.
Understanding the Basics
The concept of absolute value inequalities is a fundamental mathematical concept that is often encountered in various real-world situations. Understanding the basics of absolute value inequalities is crucial for solving word problems and practical applications involving these types of equations.
An absolute value inequality is an inequality that includes the absolute value function, which represents the distance between a number and zero. It is denoted by the symbol || and can be thought of as the positive magnitude of a number, regardless of its sign.
For example:
- The absolute value of 5 is 5: |5| = 5
- The absolute value of -3 is 3: |-3| = 3
- The absolute value of 0 is 0: |0| = 0
When dealing with absolute value inequalities, it is important to understand the properties associated with this concept. One property is the triangle inequality, which states that for any two numbers a and b, the absolute value of their sum is less than or equal to the sum of their absolute values. In equation form, this can be represented as:
|a + b| ≤ |a| + |b|
This property is useful when solving word problems involving absolute value inequalities, as it can help determine the range of possible values and intervals where the inequalities hold true.
How to Solve Absolute Value Inequalities?

Absolute value inequalities involve equations that contain absolute values, which represent the distance between a number and zero on a number line. These types of inequalities can often be found in real-world scenarios where the magnitude or distance from a certain value is important.
To solve absolute value inequalities, follow these steps:
- Identify the inequality and understand its meaning in the given context.
- Isolate the absolute value expression on one side of the inequality.
- Split the inequality into two separate cases, one for when the absolute value expression is positive and one for when it is negative.
- Solve each case separately, treating the absolute value expression as a positive number in one case and as a negative number in the other case.
- Combine the solutions from the two cases to find the final solution to the absolute value inequality.
It is important to remember that when solving absolute value inequalities, there may be multiple solutions or no solution at all. It is also crucial to check the solutions in the original inequality to ensure their validity.
By following these steps and practicing solving absolute value inequalities, you can effectively handle word problems that involve absolute value inequalities and find the appropriate solutions necessary for the given context.
Step-by-Step Guide
In this step-by-step guide, we will walk through how to solve absolute value inequalities word problems. These types of problems involve finding the set of values that satisfy an inequality expression involving absolute value.
To solve these types of problems, we typically follow a series of steps:
- Identify the absolute value expression: Look for any expressions within absolute value bars, such as |x – 2|.
- Set the expression equal to zero: Set the expression inside the absolute value bars equal to zero and solve for the variable, such as x – 2 = 0.
- Solve for the variable: Solve the equation from step 2 to find the value(s) of the variable, such as x = 2.
- Formulate and solve inequalities: Use the value(s) found in step 3 to formulate and solve inequalities based on the original absolute value expression.
- Find the solution set: Identify the set of values that satisfy the inequality and represent the solution set either numerically or graphically.
By following these steps, you can approach absolute value inequalities word problems with a systematic method to find the solution set. It is important to pay attention to the specific wording and context of the problem to accurately formulate and solve the inequalities. Practice and familiarity with absolute value inequalities will help improve your problem-solving skills in this area.
Real-Life Applications of Absolute Value Inequalities
Absolute value inequalities have numerous real-life applications across various fields. These mathematical concepts are used to solve problems that involve a range of possibilities and constraints. For example, they can be used to represent and analyze situations involving distances, temperatures, and financial transactions.
In transportation planning: Absolute value inequalities help in optimizing routes and finding the shortest distance between two points. They are especially useful in logistics and delivery industries, where time and distance are critical factors. By setting up absolute value inequalities, transportation planners can determine the routes that minimize costs and maximize efficiency.
In weather forecasting: Absolute value inequalities are used to analyze temperature variations and predict weather patterns. Meteorologists often use these concepts to solve equations involving temperature differences, allowing them to make accurate predictions about how temperatures will change over time.
In finance and investment: Absolute value inequalities are employed to calculate risk and return on investments. They help investment managers determine the range of potential gains or losses based on various factors, such as interest rates, market conditions, and company performance. By setting up and solving these inequalities, investors can make informed decisions to maximize their returns and minimize their risks.
In manufacturing processes: Absolute value inequalities are used to optimize production processes and ensure quality control. They can be applied to monitor tolerances and deviations in manufacturing specifications. By setting up absolute value inequalities, engineers can determine the acceptable range of values for various parameters, such as dimensions, weights, and tolerances, to ensure that products meet the required standards.
Overall, absolute value inequalities are valuable tools in various real-life applications. They allow individuals to analyze and solve complex problems by considering a range of possibilities and constraints. By understanding and applying these mathematical concepts, individuals can make informed decisions and optimize their processes in different fields.
Word Problems and Examples
In solving absolute value inequalities word problems, it is important to understand how to translate real life situations into mathematical expressions and equations. By doing so, we can accurately represent the problem and find the appropriate solution.
Example 1: A store is having a sale on jackets. The original price of a jacket is $150. The store is offering a discount of 30%. Write an absolute value inequality to represent the cost of a jacket after the discount.
Let x represent the cost of the jacket after the discount. The absolute value inequality can be written as |x – 150| ≤ 0.3x. This represents that the difference between the original price and the discounted price is less than or equal to 30% of the discounted price.
Example 2: A car rental company charges $50 per day for renting a car. They also charge a flat fee of $20 for insurance. Write an absolute value inequality to represent the total cost of renting a car for x days.
Let y represent the total cost of renting a car for x days. The absolute value inequality can be written as |y – 50x – 20| ≤ 0. This represents that the difference between the cost and the equation 50x + 20 is less than or equal to 0, indicating that the cost is either equal to or less than the equation.
- Overall, absolute value inequalities word problems require a good understanding of translating real life situations into mathematical expressions. By mastering this skill, it becomes easier to solve these types of problems and find appropriate solutions.
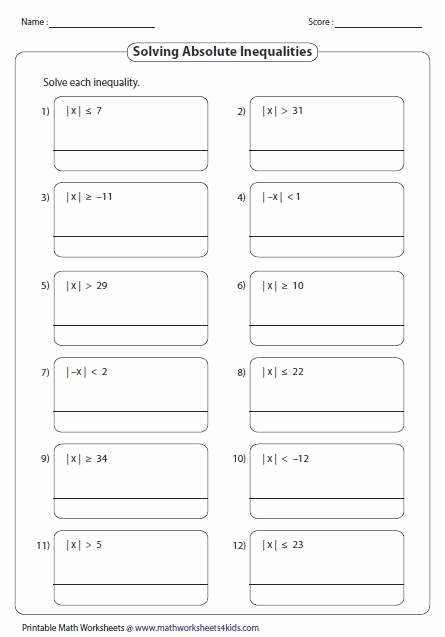
Practicing Absolute Value Inequalities
Now that we have learned about absolute value inequalities and how to solve them, it’s time to practice what we have learned. Practicing absolute value inequalities is crucial to improving your skills and gaining confidence in solving these types of equations.
Here are some tips to keep in mind while practicing absolute value inequalities:
- Remember the properties of absolute value: |a| ≥ 0 and |a| = -a if a ≤ 0.
- When solving absolute value inequalities, always isolate the absolute value term on one side of the inequality symbol.
- Consider both cases: x – a > b or x – a < -b. Solve both inequalities separately.
- After solving the two inequalities, combine the solutions to find the final solution for the absolute value inequality.
- Remember to check your solution by substituting it back into the original inequality to ensure it satisfies the inequality.
Now that you are aware of these tips, it’s time to put them into practice. Solve the absolute value inequality problems provided in the worksheet with answers (PDF) format. Use the steps you have learned to find solutions to each problem. Once you have solved the problems, refer to the answers provided to check your work.
Practicing absolute value inequalities regularly will help you become more comfortable with these types of equations and improve your problem-solving skills. Remember to review the concepts and techniques whenever you face difficulties. With practice, you’ll be able to solve absolute value inequalities confidently and accurately.