
Preparing for a mid-year test can be a daunting task, especially when it comes to a subject like algebra. With its complex equations and abstract concepts, algebra can easily leave students feeling overwhelmed and confused. However, with the right study guide, you can approach your mid-year test with confidence and a solid understanding of the material.
This study guide is designed to help you review key topics and concepts that are commonly tested in Algebra 1 mid-year exams. It covers a range of topics, including solving equations, graphing functions, and working with exponents and polynomials. Each topic is broken down into manageable sections, with step-by-step explanations and practice problems to reinforce your understanding.
Whether you’re struggling with a specific topic or just need a comprehensive review, this study guide will provide you with the tools you need to succeed on your Algebra 1 mid-year test. By dedicating time to studying and practicing the material, you’ll not only increase your chances of earning a high score, but you’ll also develop a solid foundation for future algebraic studies.
Algebra 1 Mid Year Test Study Guide
Preparing for the Algebra 1 Mid Year Test can be daunting, but with the right study guide, you can feel confident and ready on exam day. This study guide will provide you with the key concepts and topics that are likely to be covered on the test, allowing you to focus your study efforts efficiently.
1. Linear Equations and Inequalities: Be prepared to solve linear equations and inequalities, both graphically and algebraically. Understand how to represent these equations and inequalities on a coordinate plane and interpret their solutions.
2. Functions: Know the difference between a relation and a function, and be able to determine if a given relation is a function. Understand function notation and how to evaluate functions for specific inputs. Be able to analyze and graph functions.
3. Systems of Equations and Inequalities: Be familiar with different methods of solving systems of linear equations, such as graphing, substitution, and elimination. Understand how to solve systems of inequalities and interpret their solutions graphically.
4. Exponents and Radicals: Be comfortable simplifying expressions with exponents and radicals. Understand the properties of exponents and how to apply them in various situations. Know how to simplify and solve equations involving radicals.
5. Polynomials: Be able to perform operations with polynomials, including addition, subtraction, multiplication, and division. Understand how to factor polynomials and solve quadratic equations.
6. Quadratic Functions: Understand the properties and characteristics of quadratic functions, including vertex form, standard form, and factored form. Be able to graph quadratic functions and solve quadratic equations using various methods.
7. Rational Expressions: Be familiar with simplifying and performing operations with rational expressions. Understand how to solve equations involving rational expressions.
8. Data Analysis and Probability: Be able to analyze and interpret data sets, including measures of central tendency, dispersion, and correlation. Understand basic concepts of probability and how to calculate probabilities.
- Note: This study guide is not exhaustive, and it’s important to review all the material covered in your Algebra 1 course. Use this guide as a starting point and consult your textbook, class notes, and any additional resources to ensure comprehensive preparation for the Mid Year Test.
Understanding Basic Algebraic Concepts

Algebra is a branch of mathematics that deals with symbols and the rules for manipulating those symbols. It is a fundamental concept that helps us solve problems and understand relationships between variables. In algebra, letters or symbols are used to represent unknown quantities, and equations are used to express relationships between these quantities.
Variables are the basic building blocks of algebra. A variable is a symbol that represents an unknown quantity. It can be any letter or symbol, such as x or y. Variables allow us to represent unknowns in equations and solve for their values.
Expressions are combinations of numbers, variables, and operations. They represent mathematical phrases and can be simplified or evaluated. An example of an expression is 2x + 3, where 2 and 3 are coefficients, x is the variable, and + is the operation.
Equations are mathematical statements that consist of two expressions separated by an equal sign (=). They express the equality of two quantities. Solving equations involves finding the value of the variable that makes the equation true.
Functions are special types of equations that have a specific input and output relationship. They are represented by a rule or formula and can be graphed on a coordinate plane. Functions are an important concept in algebra as they help us analyze and model real-world situations.
Overall, understanding these basic algebraic concepts is crucial for solving problems, analyzing patterns, and making sense of the world around us. With a solid foundation in algebra, we can tackle more complex mathematical concepts in higher levels of education and apply algebraic reasoning to various fields of study.
Solving Linear Equations

Linear equations are equations that involve variables raised to the power of 1. Solving linear equations is an important skill in algebra as it allows us to find the value of the variable that satisfies the equation. There are different methods that can be used to solve linear equations, including simplifying, isolating the variable, and using inverse operations.
One method for solving linear equations is simplifying. This involves combining like terms and using the distributive property to simplify the equation. By simplifying the equation, we can make it easier to isolate the variable on one side of the equation.
Another method for solving linear equations is isolating the variable. This involves manipulating the equation to get the variable by itself on one side and the constants on the other side. This can be done by adding or subtracting the same value to both sides, or by multiplying or dividing both sides by the same value.
Example:
Let’s solve the equation: 2x + 3 = 9
- Start by simplifying the equation by combining like terms: 2x + 3 = 2x + 6
- Isolate the variable by subtracting 2x from both sides: 3 = 6
- Subtract 3 from both sides to solve for x: x = 3
Using these methods, we can solve linear equations and find the value of the variable that satisfies the equation. It’s important to check our solution by substituting it back into the original equation to ensure that it is correct.
Working with Inequalities
When studying algebra, one important concept to understand is working with inequalities. Inequalities are mathematical statements that compare two quantities and indicate whether one is greater than, less than, or equal to the other. Inequalities are denoted by symbols such as < (less than), > (greater than), ≤ (less than or equal to), and ≥ (greater than or equal to).
When solving inequalities, it is important to remember the rules of algebra. Just like solving equations, you can add, subtract, multiply, or divide both sides of an inequality by the same value without changing the inequality. However, there is one additional rule to keep in mind: if you multiply or divide both sides of an inequality by a negative number, you must reverse the direction of the inequality symbol.
Inequalities can also be represented graphically on a number line. For example, if you have an inequality x < 5, you would represent it on a number line by shading the area to the left of 5. If the inequality is x > 3, you would shade the area to the right of 3. If the inequality is x ≤ 2, you would shade everything to the left of and including 2. If the inequality is x ≥ -4, you would shade everything to the right of and including -4.
It is also important to understand how to solve compound inequalities, which are inequalities that involve more than one inequality. You can solve a compound inequality by solving each inequality separately and then combining the solutions. For example, to solve the compound inequality 2x + 3 > 7 and 4x – 1 < 11, you would solve each inequality separately and then find the overlap of the solutions.
Graphing Linear Functions

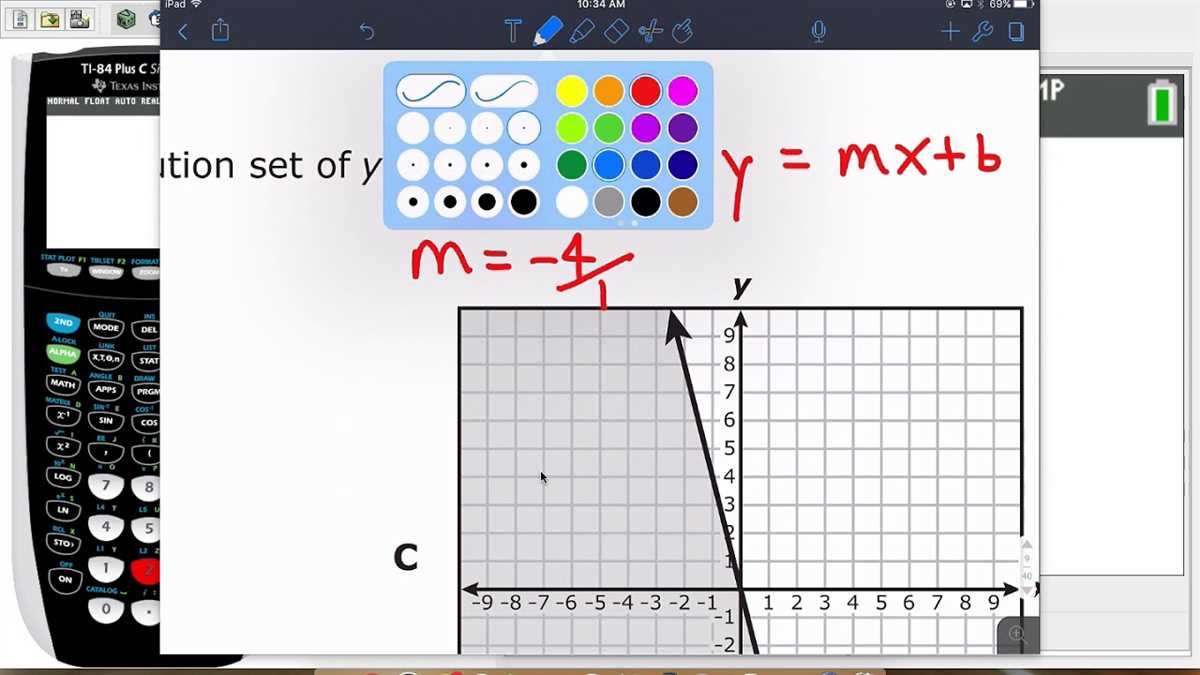
A linear function is a mathematical equation that can be graphed as a straight line. It consists of two variables, x and y, and can be expressed in the form y = mx + b, where m is the slope of the line and b is the y-intercept. Graphing linear functions can help us visualize and understand the relationship between the variables.
To graph a linear function, we need to plot several points on the coordinate plane and connect them with a straight line. To find the y-intercept, we set x = 0 and solve for y. This gives us one point on the graph. Then, using the slope, we can find other points by moving vertically and horizontally from the initial point.
Example: Let’s graph the linear function y = 2x + 3. We start by finding the y-intercept, which is (0, 3). Then, using the slope of 2, we can find additional points by moving 2 units up and 1 unit to the right from the y-intercept. So, our graph will include points (0, 3), (1, 5), (2, 7), and so on. Connecting these points with a straight line gives us the graph of the linear function.
Linear functions can have different slopes, which determines the steepness of the line. A positive slope indicates an upward-sloping line, while a negative slope indicates a downward-sloping line. A slope of 0 results in a horizontal line, and an undefined slope represents a vertical line. The graph of a linear function can also be shifted vertically or horizontally by adding or subtracting constants to the equation.
Summary: Graphing linear functions involves plotting points and connecting them with a straight line. The equation y = mx + b represents a linear function, where m is the slope and b is the y-intercept. Different slopes and shifts can result in various line orientations and positions on the coordinate plane.
| Vocabulary | Definition |
|---|---|
| Slope | The steepness of a line |
| Y-intercept | The point where the line intersects the y-axis |
| Horizontal line | A line parallel to the x-axis with a slope of 0 |
| Vertical line | A line parallel to the y-axis with an undefined slope |
| Shift | To move the graph horizontally or vertically |
Simplifying and Evaluating Algebraic Expressions
Simplifying and evaluating algebraic expressions is an important skill in algebra that is used to make equations and formulas easier to work with. By simplifying expressions, we can eliminate unnecessary terms or combine like terms to make the expression more manageable. This allows us to solve equations and perform calculations more efficiently.
When simplifying algebraic expressions, it is important to follow the rules of order of operations, which states that we must perform operations inside parentheses first, then exponents, then multiplication and division from left to right, and finally addition and subtraction from left to right. By applying these rules, we can simplify complex expressions step by step and arrive at a simplified form.
In addition to simplifying algebraic expressions, we also need to be able to evaluate them. Evaluation involves plugging in specific values for variables and solving the expression to find the numerical result. This is useful in real-life applications of algebra, where we may need to find the value of an expression given certain inputs.
An important concept in simplifying and evaluating algebraic expressions is that of like terms. Like terms have the same variable raised to the same exponent. By combining like terms, we can simplify expressions and eliminate unnecessary repetition. This is done by adding or subtracting the coefficients (numbers in front of the variables) while keeping the variables and exponents the same.
Summary:
- Simplifying algebraic expressions involves eliminating unnecessary terms or combining like terms.
- Order of operations must be followed when simplifying expressions.
- Evaluating expressions involves plugging in specific values for variables and solving for the result.
- Combining like terms is an important step in simplifying expressions.
Applying Algebraic Concepts to Real-World Problems
Algebra is not just a theoretical subject taught in classrooms. It is a powerful tool that can be used to solve real-world problems and make informed decisions. By understanding algebraic concepts and applying them to practical situations, we can analyze data, make predictions, and solve complex problems.
One of the key skills in applying algebra to real-world problems is translating verbal descriptions into mathematical equations. This involves identifying the variables, operations, and relationships between them. For example, if we are given a problem about buying groceries, we can use algebra to determine the total cost based on the quantity of items purchased and their individual prices.
Another way algebra can be applied is in analyzing patterns and trends. By graphing data and using mathematical models, we can make predictions and draw conclusions. For instance, we can use algebra to analyze population growth, financial investments, or even the spread of a virus. By understanding the underlying patterns, we can make informed decisions and plan for the future.
In conclusion, applying algebraic concepts to real-world problems is an essential skill that enables us to make sense of the world around us. By using algebra, we can analyze data, make predictions, and solve complex problems. Whether it’s calculating the cost of groceries, analyzing trends, or making informed decisions, algebra provides us with the tools to understand and solve real-world problems.