
Algebra 2 is a challenging subject for many students, but it is also an essential one for understanding higher-level math and science concepts. Unit 2 focuses on quadratic functions and their properties, including finding the vertex, factoring, and solving quadratic equations. This review answer key will help students to check their work and improve their understanding of the material.
The review answer key is divided into sections corresponding to different topics within Unit 2. Each section includes a set of practice problems and their solutions. By comparing their own answers with the provided solutions, students can identify any mistakes they may have made and learn from them. This process of self-assessment is crucial for mastering algebraic concepts.
In addition to the answer key, this review also includes explanations and examples to help students understand the underlying concepts. These explanations break down the steps involved in solving each type of problem and provide tips and tricks for making the process easier. By gaining a deeper understanding of the material, students will be better prepared to tackle more advanced topics in algebra and beyond.
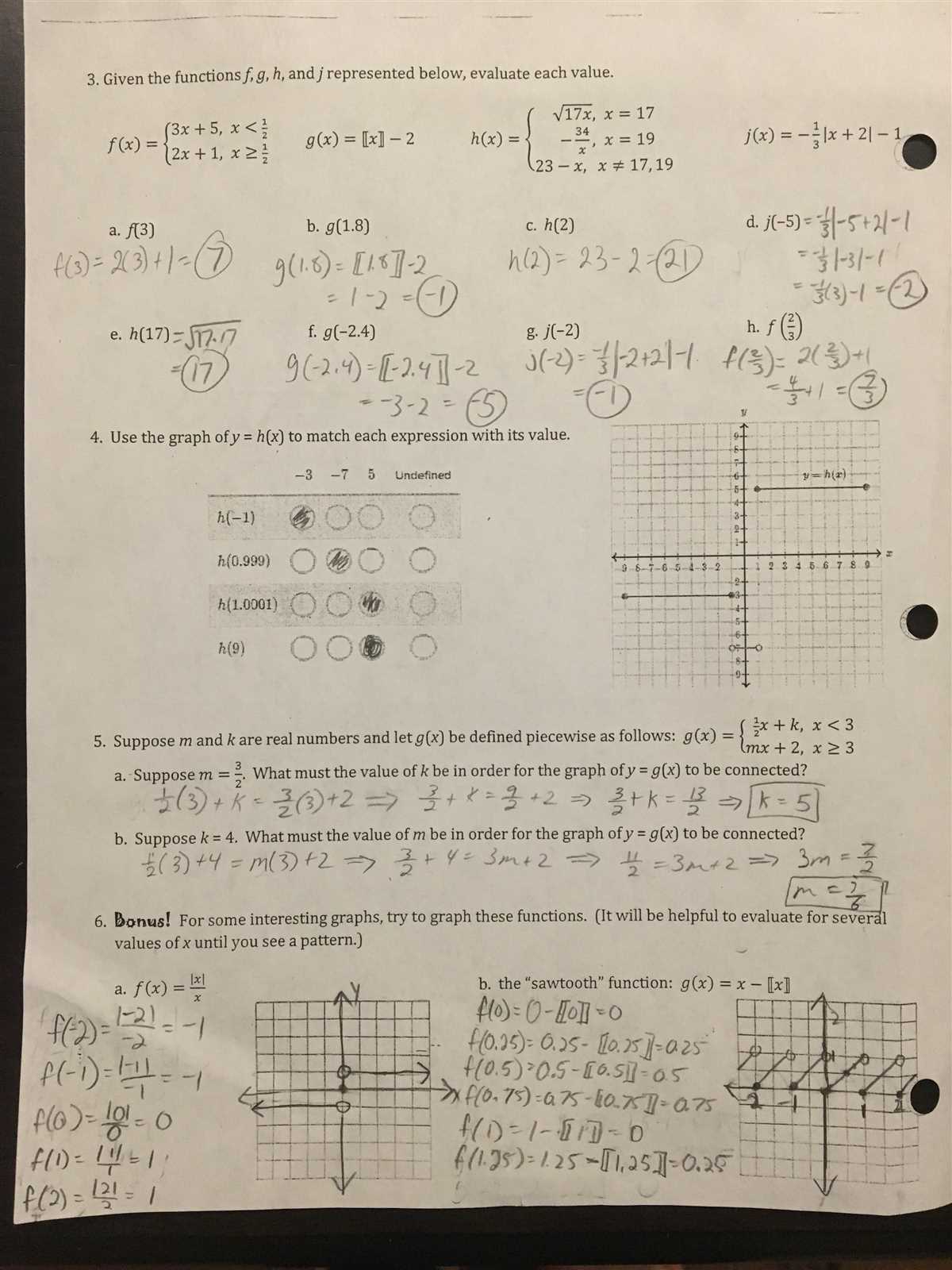
Algebra 2 Unit 2 Review Answer Key
Here is the answer key for the review questions in Unit 2 of Algebra 2. This review is designed to help you prepare for the upcoming test and assess your understanding of the material covered in this unit.
Question 1:
- Solve the equation 2x + 5 = 15.
- Step 1: Subtract 5 from both sides: 2x = 10.
- Step 2: Divide both sides by 2: x = 5.
Question 2:
- Simplify the expression (3x^2 + 5x + 2) + (2x^2 – 3x + 1).
- Step 1: Combine like terms: 5x^2 + 2x + 3.
Question 3:
- Factor the expression x^2 + 4x + 4.
- Step 1: Find two numbers that multiply to give 4 and add to give 4. In this case, the numbers are 2 and 2.
- Step 2: Rewrite the expression as (x + 2)(x + 2).
Question 4:
- Graph the equation y = 3x – 2.
- Step 1: Choose two values for x and solve for y. For example, if we choose x = 0, then y = -2. If we choose x = 1, then y = 1. This gives us the points (0, -2) and (1, 1).
- Step 2: Plot these points on a graph and draw a line through them. The line should have a slope of 3 and a y-intercept of -2.
Continue answering the remaining questions in the review using the provided answer key. Make sure to show your work and double-check your answers. Good luck!
Overview of Unit 2 Review

In Unit 2, we have covered various topics in Algebra 2 that are crucial for a thorough understanding of the subject. This review aims to consolidate your knowledge and skills, targeting the key concepts and problem-solving strategies that you have learned throughout this unit.
The review will cover topics such as linear equations and inequalities, systems of equations, quadratic functions and equations, exponential functions, and logarithmic functions. These topics are essential in Algebra 2 as they lay the foundation for more advanced concepts and applications in mathematics.
Linear equations and inequalities: You will review solving linear equations, graphing linear equations, and finding the slope and y-intercept of a line. Additionally, you will brush up on solving linear inequalities and representing them graphically.
Systems of equations: This section of the review will focus on solving systems of linear equations using various methods, including graphing, substitution, and elimination. You will also learn how to interpret the solutions to systems of equations in real-world contexts.
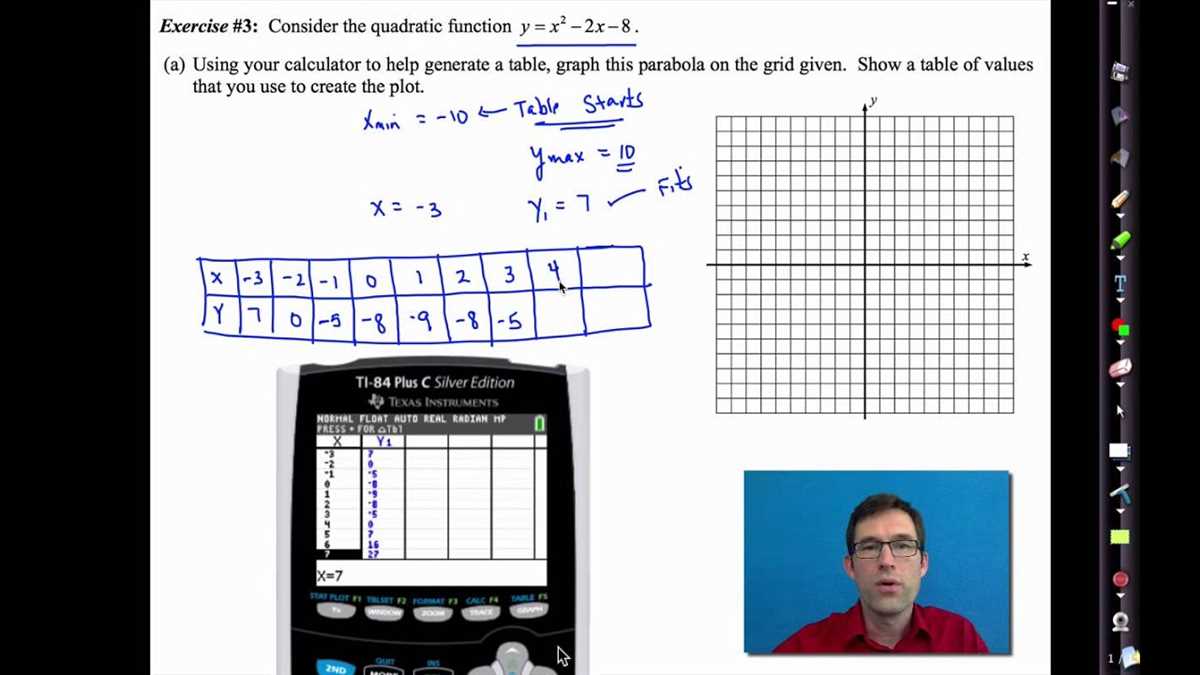
Quadratic functions and equations: You will revisit quadratic functions, including finding the vertex, axis of symmetry, and x-intercepts. Additionally, you will review solving quadratic equations using factoring, the quadratic formula, and completing the square.
Exponential functions: The review will cover exponential functions, including identifying their key features, graphing them, and solving exponential equations. You will also learn about exponential growth and decay.
Logarithmic functions: Finally, you will review logarithmic functions and their properties, graphing logarithmic functions, and solving logarithmic equations. This section will deepen your understanding of the relationship between exponential and logarithmic functions.
- Review linear equations and inequalities
- Practice solving systems of equations
- Refresh your knowledge of quadratic functions and equations
- Work on exponential functions and their applications
- Review logarithmic functions and their properties
This review will give you the opportunity to reinforce your understanding of the key concepts and problem-solving techniques in Algebra 2 Unit 2. It is important to engage in regular practice and seek clarification on any areas where you may need additional support. Good luck!
Key Concepts in Algebra 2 Unit 2
Algebra 2 Unit 2 introduces several key concepts that build upon the foundational understanding of algebraic expressions and equations. In this unit, students will explore functions, their graphical representations, and various forms of function notation.
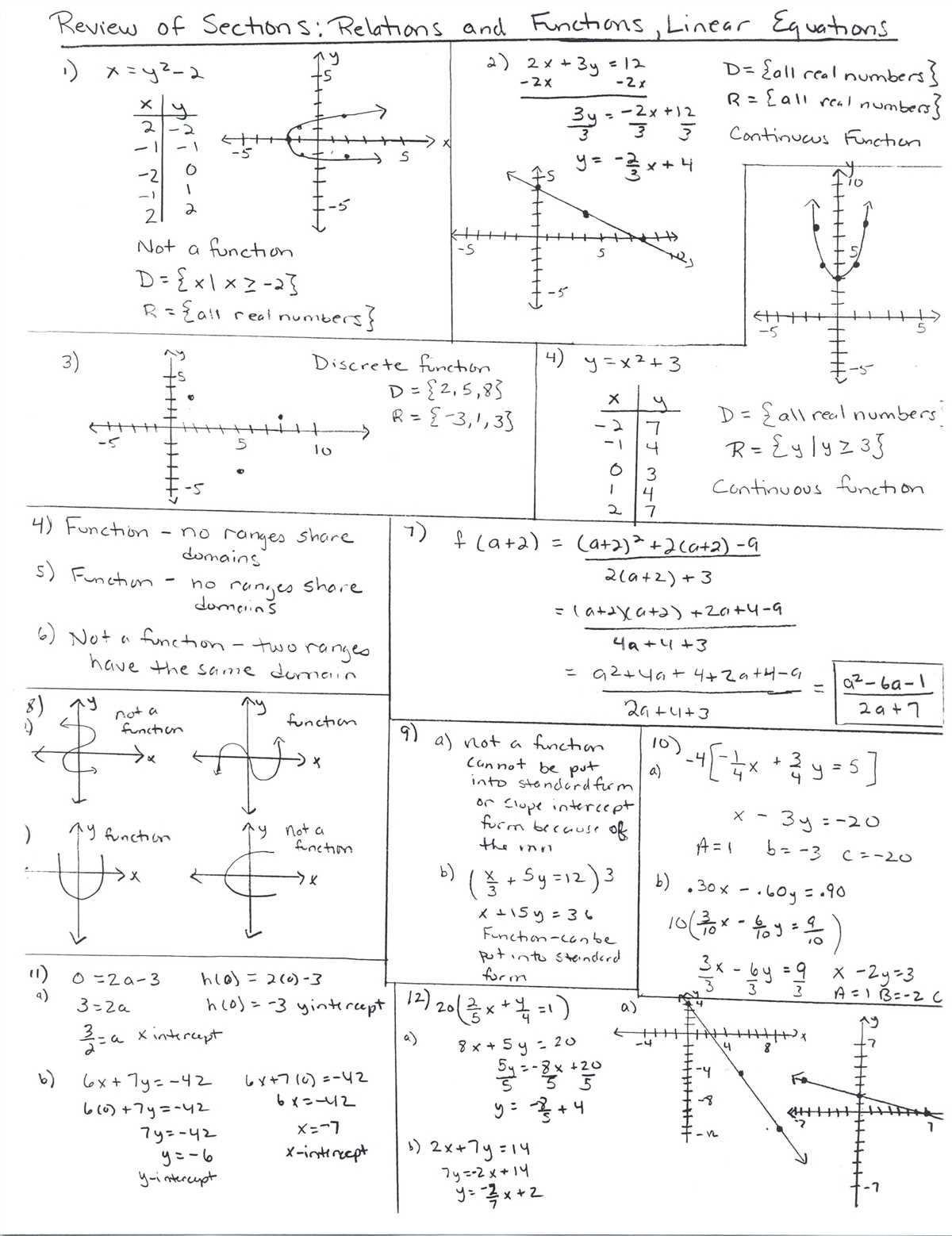
One of the key concepts in Unit 2 is the idea of a function. A function is a relationship between two sets of numbers where each input value (x-value) is associated with only one output value (y-value). Functions can be represented in different forms, such as equations, tables, graphs, or verbal descriptions. It is important to understand how to identify functions and determine whether a given relationship is a function or not.
Another important concept in this unit is the different representations of functions. Students will learn to translate functions between various forms, such as from a graph to an equation or from an equation to a table. They will also learn how to analyze and interpret key features of functions, such as domain, range, intercepts, and end behavior. Understanding these different representations and features of functions will allow students to solve problems and make predictions using algebraic reasoning.
Additionally, this unit introduces function notation, which allows for a more concise and organized way to represent functions. Function notation uses a specific notation, such as f(x), to represent the output value (y-value) corresponding to a given input value (x-value). This notation helps to simplify expressions and equations involving functions and allows for more efficient communication of mathematical ideas.
Overall, Algebra 2 Unit 2 is foundational for developing a deeper understanding of functions and their representations. By mastering these key concepts, students will be better equipped to solve complex problems involving functions and apply algebraic thinking in real-world scenarios.
Common Mistakes to Avoid in Unit 2 Review
Unit 2 in Algebra 2 covers a wide range of topics, from linear equations and inequalities to quadratic functions and polynomials. As you review for the unit test, it’s important to be aware of common mistakes that students often make. Avoiding these mistakes will help you solve problems correctly and improve your overall understanding of the material. Here are some common mistakes to watch out for:
1. Mistaking the slope-intercept form for the standard form of a linear equation:
One common mistake students make is mixing up the slope-intercept form (y = mx + b) and the standard form (Ax + By = C) of a linear equation. Remember that the slope-intercept form gives you the slope and y-intercept of a line, while the standard form is useful for finding the x-intercept and y-intercept. Double-check your equations to ensure you’re using the correct form.
2. Forgetting to apply the order of operations correctly:
Another common mistake is incorrectly applying the order of operations when simplifying expressions or solving equations. Remember the acronym PEMDAS (Parentheses, Exponents, Multiplication/Division, Addition/Subtraction) to help you remember the correct order in which to solve mathematical operations. Take your time and carefully follow each step to avoid errors.
3. Misusing the quadratic formula:
The quadratic formula (x = (-b ± √(b^2 – 4ac)) / 2a) is a useful tool for solving quadratic equations, but students often make mistakes when using it. One common error is forgetting to distribute the negative sign when simplifying the formula. Another mistake is misinterpreting the discriminant (b^2 – 4ac) and not recognizing when the equation has real or imaginary solutions. Always double-check your work and pay attention to signs and variables.
4. Neglecting to check for extraneous solutions:
When solving equations or inequalities, it’s important to check your answers to ensure they satisfy the original problem. Sometimes, students forget this step and end up with extraneous solutions. These are solutions that do not actually work in the context of the problem. Always substitute your solutions back into the original equation or inequality to make sure they are valid.
By avoiding these common mistakes, you can approach the unit 2 test with confidence and have a better chance of achieving a successful outcome. Practice regularly, seek help when needed, and remember to take your time and double-check your work. Good luck!
Tips for Understanding Algebra 2 Unit 2
Algebra 2 Unit 2 can be a challenging topic, but with the right approach and study techniques, you can successfully navigate through it. Here are some tips to help you understand Unit 2 better:
1. Review the basics
Before diving into more complex concepts in Unit 2, make sure you have a solid foundation in algebraic fundamentals. Review the basic concepts of variables, equations, and operations to ensure you are starting from a strong base.
2. Understand the language
Mathematics, including algebra, has its own set of vocabulary and symbols. Take the time to understand and familiarize yourself with the language used in Unit 2. This will make it easier for you to follow the lessons and grasp new concepts.
3. Work through examples

Practice is key to understanding algebraic concepts. Work through plenty of example problems and practice exercises to reinforce your knowledge and build your problem-solving skills. Pay attention to the steps and reasoning behind each solution.
4. Seek help when needed
If you find yourself struggling with a particular concept or problem, don’t hesitate to seek help. Talk to your teacher, classmates, or find online resources and tutorials to get additional support. Sometimes a different perspective can make all the difference in understanding a difficult concept.
By applying these tips and staying consistent with your studies, you can improve your understanding of Algebra 2 Unit 2. Remember to stay patient and keep practicing, as algebra is a subject that requires continuous effort and practice to master.
Sample Questions and Answers from Unit 2 Review
Here are some sample questions and answers from the Unit 2 review in Algebra 2. These questions cover various topics and concepts that were taught throughout the unit.
1. Simplify the expression (3x^2 – 2x + 1) + (2x^2 + 4x – 3).
To simplify this expression, we need to combine like terms. So, we can add the coefficients of the same degree terms and keep the variable part unchanged. In this case, we have:
- 3x^2 + 2x^2 = 5x^2
- -2x + 4x = 2x
- 1 – 3 = -2
Therefore, the expression simplifies to 5x^2 + 2x – 2.
2. Solve the equation 2(x + 3) = 4x – 2.
To solve this equation, we need to isolate the variable x. We can start by distributing the 2 on the left-hand side:
2x + 6 = 4x – 2
Next, we can subtract 2x from both sides to get rid of the x term on the left-hand side:
6 = 2x – 2
Now, we can add 2 to both sides to isolate the variable:
8 = 2x
Finally, we divide both sides of the equation by 2 to solve for x:
x = 4
So, the solution to the equation is x = 4.
These are just a couple of examples of the types of questions you can expect to see on the Unit 2 review in Algebra 2. Make sure to review all the concepts covered in the unit to prepare yourself for the exam.
Next Steps: How to Prepare for the Algebra 2 Unit 2 Test
Now that you have reviewed the Algebra 2 Unit 2 materials, it’s time to start preparing for the upcoming test. Here are some next steps you can take to ensure that you are ready for the exam:
- Review your notes: Go through your class notes and make sure you understand all the concepts and examples covered in Unit 2. Pay attention to any areas where you feel unsure or have questions.
- Practice problems: Solve a variety of practice problems related to the topics covered in Unit 2. This will help you reinforce your understanding and improve your problem-solving skills.
- Work on sample tests: Find sample tests or past exam papers for Unit 2 and attempt them under timed conditions. This will give you a sense of the format and types of questions you can expect on the actual test.
- Seek help if needed: If you are struggling with any of the topics or concepts, don’t hesitate to seek help from your teacher, classmates, or online resources. It’s important to address any areas of confusion before the test.
- Review and revise: Go through your practice problems and sample tests to identify any mistakes or areas of improvement. Take the time to revise these topics and ensure that you have a solid understanding of them.
By following these steps, you will be well-prepared for the Algebra 2 Unit 2 test. Remember to manage your time effectively and stay focused during the exam. Good luck!