Are you struggling to understand how to calculate the area of regular polygons? Look no further! This article provides a comprehensive worksheet with answers to help you grasp this concept easily and efficiently.
A regular polygon is a polygon with all sides and angles equal. Understanding how to find the area of regular polygons is crucial in various fields, such as architecture, engineering, and geometry. This worksheet will guide you through step-by-step instructions and provide practical exercises to strengthen your knowledge and problem-solving skills.
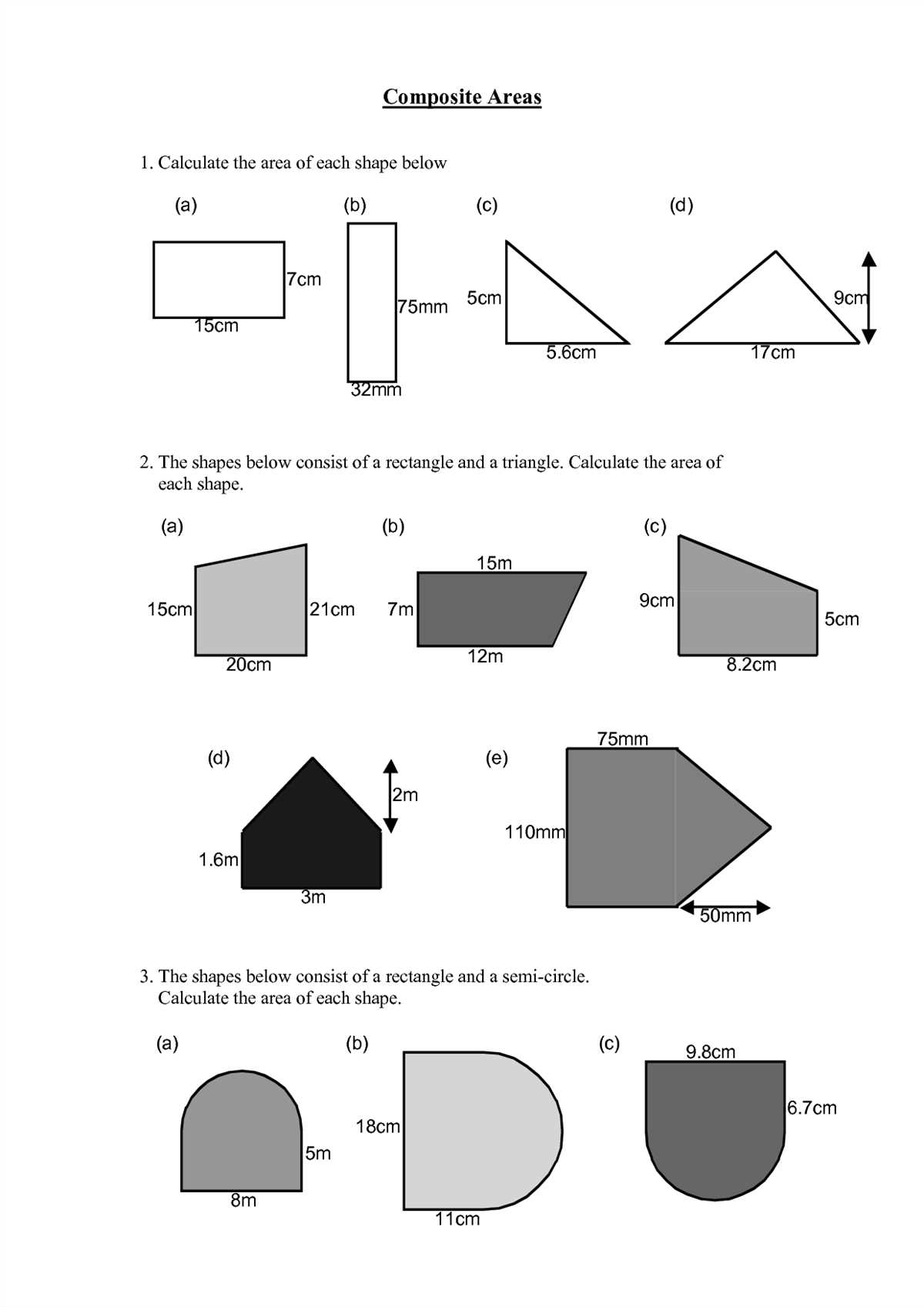
Within the worksheet, you’ll find a variety of regular polygons, such as triangles, squares, pentagons, hexagons, and octagons. Each polygon has a specific formula to calculate its area, and our answers will allow you to check your solutions for accuracy and understanding.
Whether you’re a student looking to improve your math skills or a teacher searching for additional resources for your geometry class, this worksheet is perfect for you. It covers the fundamental concepts of regular polygons and will give you the confidence to tackle more complex problems in the future. So, grab a pen and start exploring the world of regular polygons and their areas!
What Is an Area of Regular Polygons Worksheet, and Why Is It Important?

Regular polygons are geometric figures that have equal sides and angles. Examples of regular polygons include squares, equilateral triangles, and hexagons. The area of a regular polygon refers to the amount of space it occupies within its boundaries. In mathematics, calculating the area of regular polygons is an essential skill that students learn, and an area of regular polygons worksheet helps them practice and reinforce this concept.
An area of regular polygons worksheet typically consists of various problems where students are required to find the area of different regular polygons. These worksheets often provide the necessary formulas and instructions to help students solve the problems. By working through these worksheets, students can develop their understanding of the formulas and rules related to finding the area of regular polygons.
Completing an area of regular polygons worksheet is important for several reasons. Firstly, it helps students become familiar with the different types of regular polygons and their respective formulas for finding their areas. This knowledge is valuable because it provides a foundation for further mathematical concepts and problem-solving abilities.
Secondly, solving problems on an area of regular polygons worksheet improves students’ problem-solving skills and critical thinking abilities. They are required to apply formulas and strategies to find the correct answers, which helps them develop logical reasoning and analytical thinking skills.
Lastly, practicing with an area of regular polygons worksheet allows students to reinforce their understanding and mastery of the topic. By solving multiple problems, students gain confidence in their abilities and become more proficient in calculating the area of regular polygons.
Understanding Regular Polygons

Regular polygons are geometric shapes that have equal side lengths and equal angles. They have a predictable and symmetrical pattern, making them easy to identify and work with. Understanding regular polygons is essential in various mathematical and geometric concepts.
Definition: A regular polygon is a polygon with all sides and angles congruent, or equal. In simpler terms, it is a shape with equal sides and equal angles. The most common examples of regular polygons are triangles, squares, pentagons, hexagons, and octagons.
One of the important properties of regular polygons is that the interior angles of a regular polygon can be calculated using the formula (n – 2) * 180 degrees, where n represents the number of sides. For example, a triangle has three sides, so the sum of its interior angles is (3 – 2) * 180 = 180 degrees. Similarly, a square has four sides, so the sum of its interior angles is (4 – 2) * 180 = 360 degrees.
Calculating the area: To find the area of a regular polygon, you need to know the side length and the apothem, which is the perpendicular distance from the center of the polygon to any side. The formula for calculating the area of a regular polygon is (1/2) * perimeter * apothem. Once you have the side length and apothem, you can easily calculate the area.
Applications: Regular polygons have numerous applications in different fields such as architecture, design, and engineering. Architects often use regular polygons, especially hexagons, to design buildings with maximum stability and strength. Regular polygons also appear in various art forms and patterns, adding aesthetic value to designs. Moreover, regular polygons play a crucial role in computer graphics, where they are used to create realistic shapes and structures.
- Regular polygons have equal side lengths and equal angles.
- The interior angles of a regular polygon can be calculated using the formula (n – 2) * 180 degrees.
- The area of a regular polygon can be found using the formula (1/2) * perimeter * apothem.
- Regular polygons have applications in architecture, design, and computer graphics.
The Concept of Area in Regular Polygons
In geometry, the concept of area refers to the measurement of the two-dimensional space occupied by a shape or figure. Regular polygons are a specific type of polygon where all sides and angles are equal. The area of a regular polygon can be calculated using various formulas, depending on the number of sides it has and the length of its sides.
To calculate the area of a regular polygon with n sides, the formula is: Area = (n * s^2) / (4 * tan π/n), where s represents the length of each side and π represents the mathematical constant pi.
For example, let’s consider a regular hexagon with side length 6 units. Using the formula, we can calculate its area as follows:
Area = (6 * 6^2) / (4 * tan π/6) = 18√3 square units
The area of regular polygons can also be calculated by dividing them into smaller, known shapes, such as triangles, and summing up their individual areas. This method is especially useful when dealing with irregular polygons that cannot be easily divided into uniform shapes.
Understanding the concept of area in regular polygons is important in various fields, such as architecture, engineering, and design. It allows us to calculate the space required by certain structures or objects and make informed decisions based on their dimensions.
Using Formulas to Calculate the Area of Regular Polygons
Calculating the area of regular polygons can be done using specific formulas that depend on the characteristics of the shape. Regular polygons have equal sides and equal angles, making them easier to work with when it comes to finding their area. By understanding and using these formulas, mathematicians and researchers can accurately determine the area of regular polygons.
One common formula used to calculate the area of regular polygons is the formula for the area of a regular polygon with side length ‘s’ and ‘n’ number of sides. This formula is A = (n × s²) / (4 × tan(π/n)). In this formula, ‘A’ represents the area of the regular polygon, ‘n’ represents the number of sides, and ‘s’ represents the length of each side. By plugging in the appropriate values, the formula can be used to find the area of various regular polygons.
Another formula commonly used to calculate the area of regular polygons is the formula for the area of a regular polygon with radius ‘r’ and ‘n’ number of sides. This formula is A = (n × r² × sin(2π/n)) / 2. In this formula, ‘A’ represents the area of the regular polygon, ‘n’ represents the number of sides, and ‘r’ represents the radius, which is the distance from the center of the polygon to a vertex. This formula can also be used to find the area of regular polygons by plugging in the appropriate values for ‘n’ and ‘r’.
In conclusion, formulas are used to calculate the area of regular polygons by taking into account the characteristics of the shape such as the length of the sides or the radius. By using these specific formulas, mathematicians and researchers can accurately determine the area of regular polygons and further their understanding of geometric properties.
Practical Examples and Exercises in the Worksheet

The worksheet on area of regular polygons provides a variety of practical examples and exercises that help students understand and apply the concept of finding the area of regular polygons. These examples and exercises challenge students to use their knowledge of the formula for finding the area of a regular polygon, which is: area = 1/2 * apothem * perimeter.
In the worksheet, students are presented with various regular polygons, such as squares, triangles, pentagons, and hexagons. Each polygon is accompanied by its dimensions, including the apothem and perimeter. Students are then asked to calculate the area of each polygon using the formula. This allows students to practice using the formula in real-world scenarios and reinforces their understanding of the concept.
The worksheet also includes a mix of multiple-choice and open-ended questions, providing students with different types of problems to solve. This helps them develop their problem-solving and critical thinking skills. Additionally, the worksheet incorporates real-life examples, such as finding the area of a soccer field or a basketball court in the shape of regular polygons. These examples make the concept more relatable and engaging for students.
Moreover, the worksheet offers answer keys for each exercise, which allows students to check their work and self-assess their understanding of the topic. The answer keys provide step-by-step explanations of how to solve each problem, ensuring that students can learn from their mistakes and improve their skills.
In conclusion, the practical examples and exercises in the area of regular polygons worksheet provide students with opportunities to apply their knowledge and practice finding the area of various regular polygons. The worksheet’s mix of problem types, real-life examples, and answer keys make it a valuable tool for students to deepen their understanding and master the concept.
Answers and Solutions to the Worksheet Questions

Below are the answers and step-by-step solutions to the questions on the area of regular polygons worksheet:
Question 1:
The worksheet begins with a question asking for the area of a regular hexagon with a side length of 8 units. To find the area, we first need to find the apothem (the distance from the center of the hexagon to one of its sides). Using the formula for the apothem, which states that the apothem is equal to the side length divided by two times the tangent of 180 degrees divided by the number of sides, we find that the apothem is approximately 6.928 units. To find the area, we multiply the apothem by the perimeter of the hexagon and divide by 2, giving us an answer of approximately 167.66 square units.
Question 2:
The second question on the worksheet asks for the area of a regular pentagon with a side length of 5 units. To find the area, we first need to find the apothem, which can be found using the same formula as in the previous question. The apothem for this pentagon is approximately 3.827 units. To find the area of the pentagon, we multiply the apothem by the perimeter of the pentagon and divide by 2, giving us an answer of approximately 19.135 square units.
Question 3:
In question 3, we are asked to find the area of a regular octagon with a side length of 6 units. Again, we start by finding the apothem using the formula mentioned earlier. The apothem for this octagon is approximately 4.899 units. To find the area, we multiply the apothem by the perimeter of the octagon and divide by 2, giving us an answer of approximately 44.056 square units.
- Question 1: Area of regular hexagon with side length 8 units: Approximately 167.66 square units.
- Question 2: Area of regular pentagon with side length 5 units: Approximately 19.135 square units.
- Question 3: Area of regular octagon with side length 6 units: Approximately 44.056 square units.
Benefits of Using an Area of Regular Polygons Worksheet
Using an area of regular polygons worksheet can be beneficial for both students and teachers. This tool provides a structured way for students to practice and apply their knowledge of finding the area of regular polygons, while also providing a resource for teachers to assess their understanding. Here are some specific benefits of using an area of regular polygons worksheet:
- Practice and Reinforcement: Worksheets allow students to practice solving a variety of problems related to finding the area of regular polygons. This repetitive practice helps reinforce their understanding of the concept and improves their problem-solving skills.
- Visual Representation: Worksheets often include visual representations of regular polygons, which can help students visualize the shape and understand how to calculate its area. This visual aid can make the concept more tangible and easier to grasp.
- Independent Learning: Worksheets can be completed independently, allowing students to work at their own pace and take ownership of their learning. They can use the worksheet as a self-assessment tool to identify areas where they need additional practice or understanding.
- Assessment: Worksheets provide teachers with a means to assess students’ understanding of finding the area of regular polygons. By reviewing their work, teachers can identify any misconceptions or areas of weakness that need to be addressed.
- Review and Homework: Worksheets can be used as a review tool to reinforce the concept of finding the area of regular polygons. They can also be assigned as homework to allow students to practice the concept outside of the classroom.
In conclusion, using an area of regular polygons worksheet can be a valuable tool for both students and teachers. It provides structured practice, visual representation, independent learning opportunities, assessment, and review. By utilizing this worksheet, students can improve their understanding and problem-solving skills, while teachers can assess their progress and address any areas of weakness. Overall, incorporating worksheets into the learning process can enhance the teaching and learning experience surrounding the area of regular polygons.