Welcome to the world of vibrations and waves! In this chapter, we will explore the fascinating phenomenon of vibrating objects and the propagation of waves. Vibrations and waves are integral to our understanding of sound, light, and many other aspects of the physical world. From the smallest particles to the largest celestial bodies, vibrations and waves play a fundamental role in how energy is transmitted and detected.
In this article, we will delve into the concepts and principles of vibrations and waves, and answer some common questions that arise when studying this topic. What causes objects to vibrate? How does a wave travel through a medium? What is the relationship between vibrations and the properties of waves, such as frequency and wavelength? These are just some of the questions we will address.
Understanding vibrations and waves is not only crucial for the study of physics, but also for various other scientific and technological fields. For example, an understanding of vibrations can help engineers design stable structures that can withstand external forces and minimize the effects of vibrations. Additionally, knowledge of waves is essential for the fields of acoustics and optics, which deal with the study of sound and light, respectively.
So, whether you’re a student trying to grasp the fundamentals of vibrations and waves, or a curious individual looking to expand your knowledge of the physical world, this article will provide you with insightful answers and explanations. Let’s dive into the rich and vibrant world of vibrations and waves!
Chapter 11 Vibrations and Waves Answers
In Chapter 11 of the physics textbook, the topic of vibrations and waves is explored in depth. This chapter delves into the fundamental concepts of oscillation, resonance, and wave behavior, and provides answers to these important questions. Understanding vibrations and waves is crucial to comprehending the behavior of numerous systems in the world around us.
The chapter begins by defining vibrations as the repeated back-and-forth or up-and-down motions of an object. It explains that vibrations can be either simple harmonic or damped, and provides equations and examples to help solve related problems. Key concepts such as period, frequency, and amplitude are also elucidated.
Next, the chapter explores resonance, which occurs when an object is forced to vibrate at its natural frequency. It explains how resonance can amplify vibrations and lead to destructive effects. The concept of resonance is then applied to various real-life examples, such as musical instruments and bridges.
The chapter further investigates wave behavior, including the characteristics of transverse and longitudinal waves. It defines terms such as wavelength, frequency, and wave speed, and provides equations and diagrams to aid in the understanding of these concepts. The chapter also examines wave interference and the phenomenon of standing waves.
In conclusion, Chapter 11 of the physics textbook provides comprehensive answers to the questions and problems related to vibrations and waves. By studying this chapter, students will gain a solid understanding of the principles and applications of these fundamental concepts, which are essential in various fields of science and engineering.
Understanding Vibrations and Waves
Vibrations and waves are fundamental concepts in the field of physics that play a crucial role in explaining various phenomena in the natural world. They are essentially the result of periodic motion, where an object or a medium oscillates back and forth around a fixed position. This motion can be described in terms of displacement, velocity, and acceleration.
When an object vibrates, energy is transferred from one point to another through a medium or field. This energy transfer can occur in different ways, such as through mechanical waves, electromagnetic waves, or even quantum mechanical waves. These waves can have various properties, such as frequency, wavelength, amplitude, and speed, which govern their behavior and characteristics.
Vibrations and waves are not limited to physical objects or particles. They can also be observed in various systems, including mechanical systems like springs and pendulums, electromagnetic systems like radio waves and light, and even quantum systems like particles and atoms. Understanding how vibrations and waves work is essential for explaining a wide range of phenomena, including sound, heat, light, and even the behavior of matter at a microscopic level.
By studying vibrations and waves, scientists and engineers can gain insights into the behavior of different systems and develop practical applications. For example, knowledge of vibrations and waves is crucial in designing efficient structures and machinery, developing communication technologies, and understanding the properties of materials in various fields such as acoustics, optics, and quantum mechanics.
In conclusion, vibrations and waves are fundamental concepts in physics that are key to understanding a wide range of phenomena in the natural world. They occur in various systems and can be described in terms of displacement, velocity, and acceleration. By studying vibrations and waves, scientists and engineers can gain insights into the behavior of different systems and develop practical applications in various fields.
The Basics of Harmonic Motion
Harmonic motion is a type of motion that repeats itself over a certain period of time. It is characterized by a restoring force that acts in the opposite direction of the displacement from the equilibrium position. This restoring force causes the object to oscillate back and forth around the equilibrium position, creating a periodic motion.
In harmonic motion, there are two important properties: amplitude and frequency. The amplitude is the maximum displacement from the equilibrium position, while the frequency is the number of oscillations per unit of time. These properties determine the behavior of the harmonic motion and can be used to describe its characteristics.
Harmonic motion can be represented mathematically using equations such as the harmonic oscillator equation or the simple harmonic motion equation. These equations describe the relationship between the displacement, velocity, acceleration, and time in harmonic motion. By solving these equations, we can determine the position, velocity, and acceleration of an object at any given time during its oscillation.
The concept of harmonic motion is widely applicable in various fields, such as physics, engineering, and music. It can be observed in systems like pendulums, springs, and waves. Understanding the basics of harmonic motion is essential for analyzing and predicting the behavior of these systems and phenomena.
Analyzing Simple Harmonic Motion
Simple harmonic motion refers to the back-and-forth vibratory motion that occurs when a restoring force is proportional to the displacement from an equilibrium position. This type of motion can be found in various systems, such as a mass-spring system or a pendulum.
When analyzing simple harmonic motion, it is important to consider several key parameters. Firstly, the amplitude of the motion represents the maximum displacement from the equilibrium position. It is measured in meters and can be thought of as the “size” of the motion.
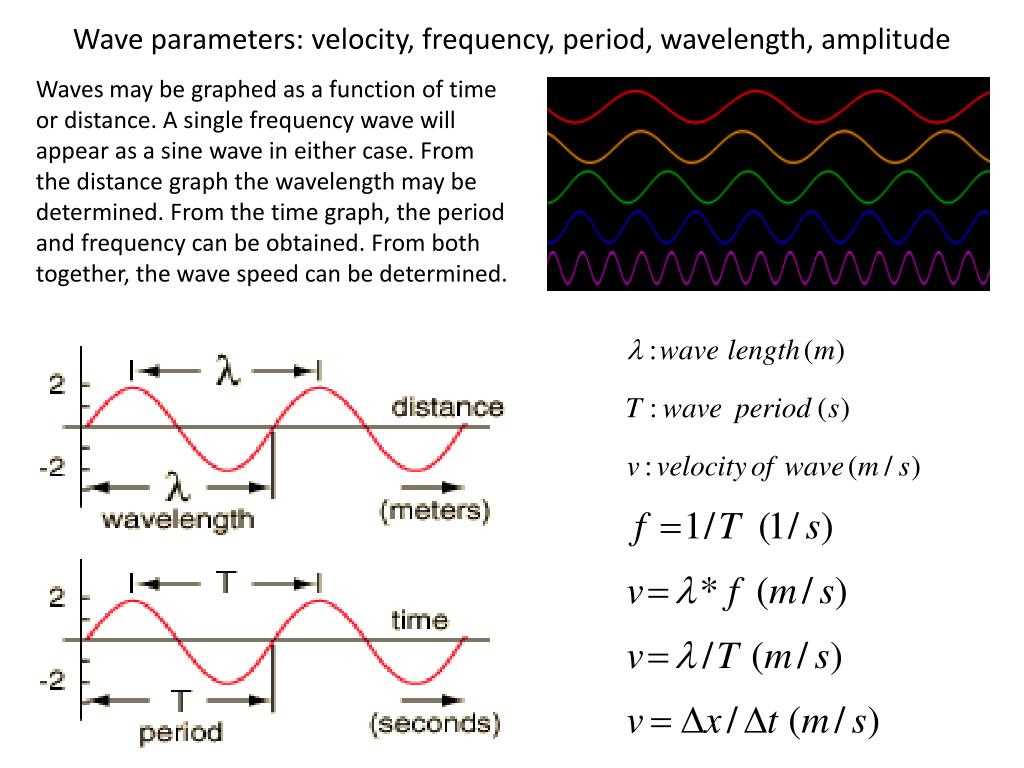
The period of the motion, denoted as T, refers to the time it takes for one complete cycle of the motion. It is measured in seconds and is related to the frequency of the motion, denoted as f, which represents the number of cycles per second. The relationship between period and frequency is given by the equation T = 1/f.
The angular frequency, denoted as ω, is another important parameter in analyzing simple harmonic motion. It is related to the period and frequency through the equation ω = 2πf = 2π/T. The angular frequency represents the rate at which the motion oscillates and is measured in radians per second.
By understanding and analyzing these parameters, one can gain a comprehensive understanding of simple harmonic motion and accurately describe its behavior and characteristics.
Exploring Resonance
In the realm of vibrations and waves, a fascinating phenomenon called resonance comes into play. Resonance occurs when an external force is applied to a system at its natural frequency, causing the system to oscillate with increased amplitude. This amplification effect is due to the synchronization of the external force with the system’s own natural frequency.
Resonance can be observed in various physical systems, such as musical instruments, buildings, and even bridges. For example, when a musician plays a specific note on a violin, the vibrations created by the strings resonate with the body of the instrument, producing a rich, sustained sound. This is possible because the frequency of the note played matches the natural frequency of the violin.
Resonance can also have destructive consequences. If a mechanical system is exposed to an external force that matches its natural frequency, the resulting vibrations can lead to catastrophic failure. This is evident in the infamous Tacoma Narrows Bridge collapse, where strong winds caused the bridge to resonate at its natural frequency, ultimately leading to its structural collapse.
To understand resonance better, it is helpful to think of it in terms of energy transfer. When the external force applies energy to the system at its natural frequency, the system absorbs and stores this energy, resulting in increased amplitude of oscillation. However, if the external force is not at the natural frequency of the system, the energy transfer is less efficient, and the oscillations dampen out over time.
Resonance plays a crucial role in various fields, including physics, engineering, and music. By understanding and harnessing the principles of resonance, scientists and engineers can design more efficient structures and systems, while musicians can create beautiful melodies and harmonies. Exploring resonance opens up a world of possibilities for understanding and manipulating the vibrational and wave nature of our universe.
Key Points:
- Resonance occurs when an external force matches the natural frequency of a system, causing increased oscillation amplitude.
- Resonance can have both constructive and destructive effects.
- Understanding resonance is important in fields such as physics, engineering, and music.
Understanding Wave Properties
Waves are a fundamental part of nature and play a significant role in our daily lives. Understanding the properties of waves is essential in various fields, including physics, engineering, and telecommunications. By examining wave properties, scientists and engineers can make predictions, develop new technologies, and solve complex problems.
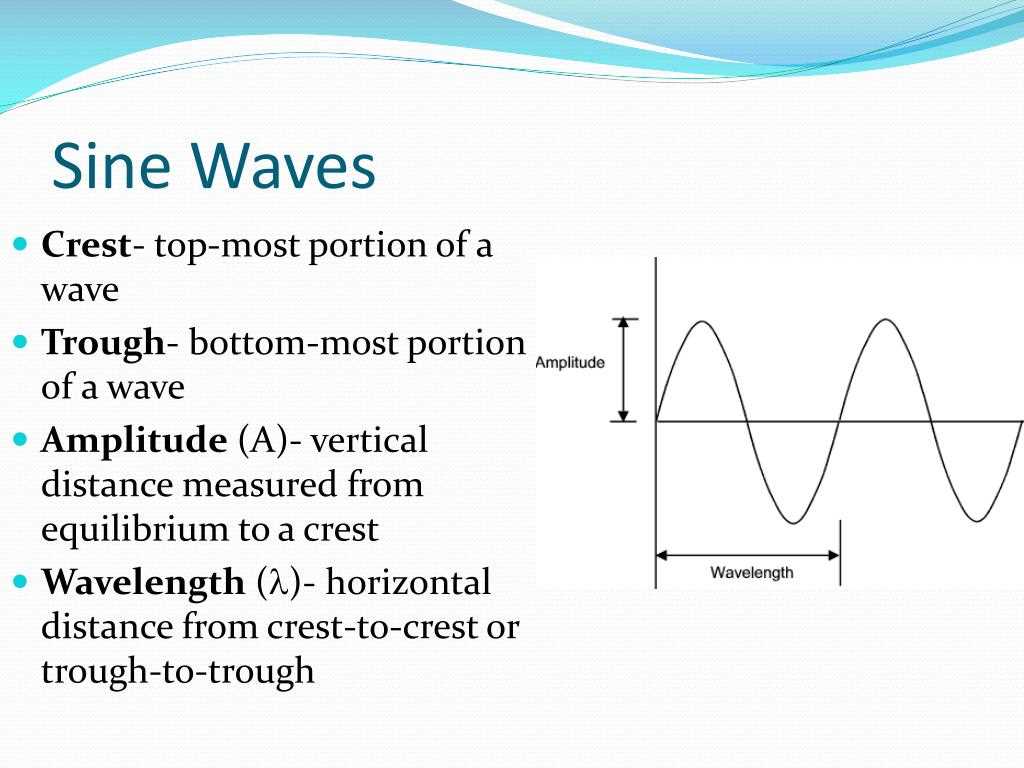
One of the key properties of waves is wavelength, which is the distance between two consecutive points in a wave that are in phase. Wavelength is typically represented by the Greek letter lambda (λ) and is measured in meters. The wavelength of a wave determines its frequency, which is the number of complete wavelengths that pass a fixed point in a given time. Frequency is measured in hertz (Hz), and it is inversely proportional to wavelength.
- Amplitude: The amplitude of a wave is the maximum displacement of particles in the medium from their rest position. It measures the energy of the wave and determines its intensity.
- Speed: The speed of a wave is the rate at which a wave travels through a medium. It is determined by the properties of the medium through which the wave is passing, such as elasticity and density.
- Reflection: When a wave encounters an obstacle or boundary, it can bounce back. This phenomenon is called reflection. The angle of incidence is equal to the angle of reflection, and the law of reflection describes this relationship.
- Refraction: Refraction occurs when a wave passes from one medium to another with a different density. As the wave enters the new medium, its speed and direction change, causing the wave to bend. The bending of waves due to refraction is responsible for various phenomena, such as the apparent bending of a straw in a glass of water.
By studying and understanding these wave properties, scientists and engineers can manipulate and control waves to improve technology and solve real-world problems. From designing efficient communication systems to developing medical imaging techniques, the knowledge of wave properties has revolutionized many aspects of our modern world.
Applying Wave Principles
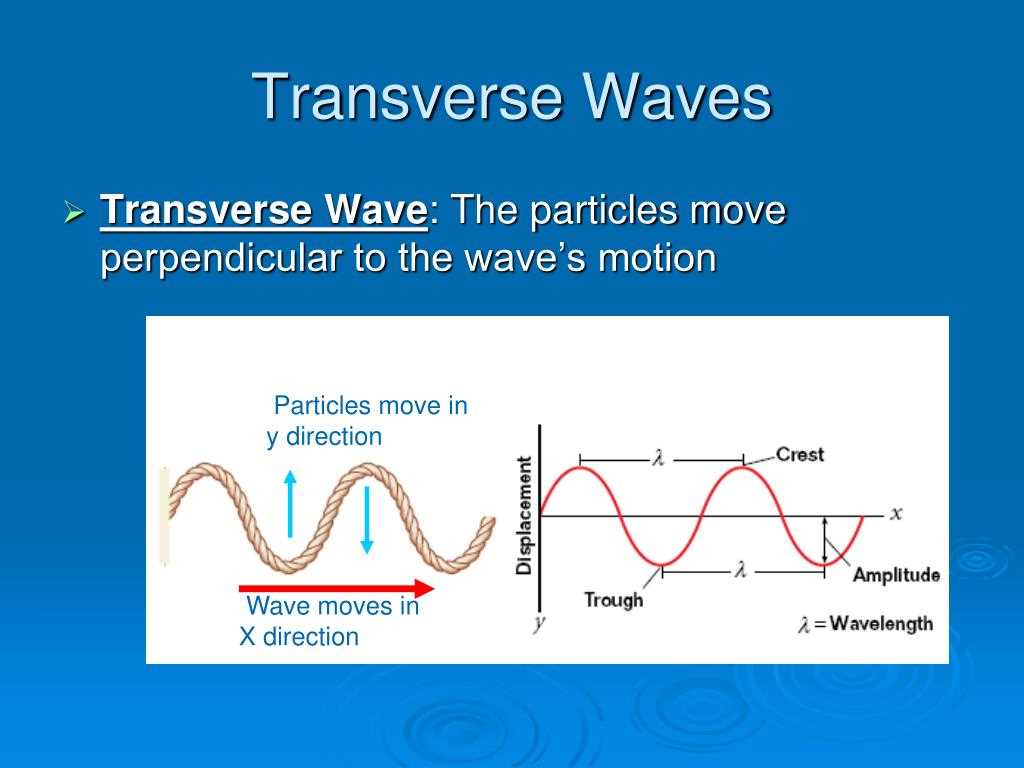
In this chapter, we have explored the fundamentals of vibrations and waves. We have discussed the basic properties of waves, such as amplitude, wavelength, frequency, and speed. We have also examined the different types of waves, including transverse waves, longitudinal waves, and standing waves.
Throughout the chapter, we have seen how these principles apply to various real-world phenomena. For example, we have learned about the behavior of waves in different mediums, such as air, water, and solids. We have also studied how waves interact with different objects and how they can be reflected, refracted, or diffracted. Additionally, we have seen how waves can interfere with each other, leading to constructive or destructive interference.
Understanding the principles of vibrations and waves is essential in various fields of science and engineering. For example, in the field of acoustics, the knowledge of wave behavior helps in designing sound systems and studying the propagation of sound waves in different environments. In optics, understanding wave properties is crucial in designing optical devices and studying the behavior of light.
Overall, this chapter has provided a solid foundation in the principles of vibrations and waves, laying the groundwork for further exploration and application in various disciplines. By understanding the fundamental concepts and properties of waves, we can begin to analyze and understand the behavior of wave phenomena in the world around us.
Key concepts covered in this chapter:
- Amplitude, wavelength, frequency, and speed of waves
- Transverse waves and longitudinal waves
- Reflection, refraction, and diffraction of waves
- Interference of waves
- Standing waves and resonance