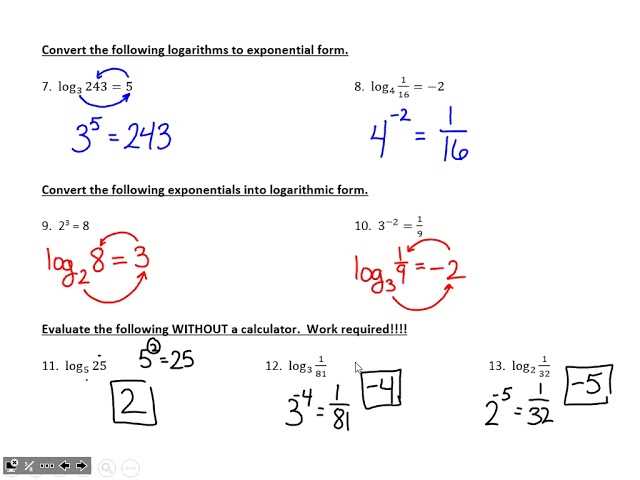
Welcome to the answer key for Chapter 2 of the polynomial and rational functions textbook! This chapter focuses on polynomial and rational functions and their properties. By understanding these functions and their graphs, you will be able to solve various types of problems and equations.
Throughout this chapter, you will explore different aspects of polynomial and rational functions, such as finding zeros, graphing functions, and understanding the behavior of functions at the ends of the graph. You will also learn how to solve equations involving these functions and how to simplify rational expressions.
This answer key will provide you with step-by-step solutions to the exercises and problems in Chapter 2. It will help you check your work, understand the concepts better, and prepare for tests and exams. Make sure to use this answer key as a tool to improve your understanding and problem-solving skills in polynomial and rational functions.
Whether you are a student looking to practice and reinforce your knowledge or a teacher in need of resources, this answer key will be a valuable companion. Get ready to dive into the world of polynomial and rational functions, and explore the power and beauty of these mathematical concepts!
Understanding Polynomials and Rational Functions
Polynomials and rational functions are essential concepts in algebra and calculus that provide valuable tools for analyzing and modeling various real-life situations. By understanding these functions and their properties, mathematicians, engineers, and scientists can solve complex equations, make predictions, and make informed decisions.
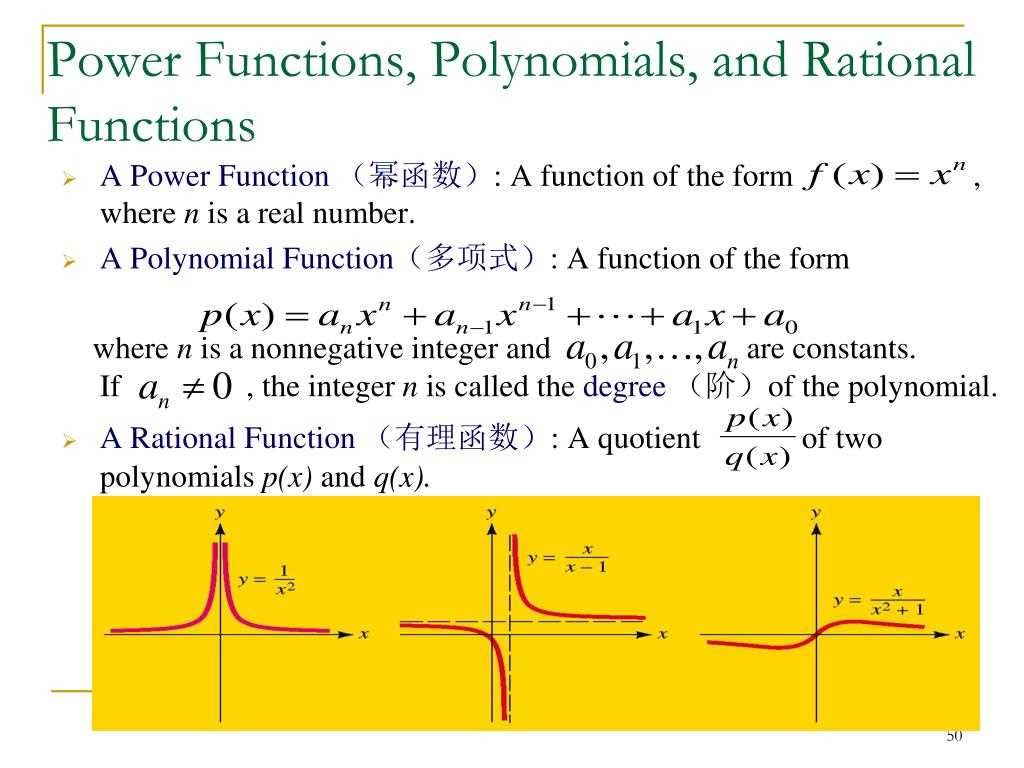
A polynomial function is a mathematical expression consisting of variables, coefficients, and exponents, combined using addition, subtraction, and multiplication. It can be written as f(x) = anxn + an-1xn-1 + … + a1x + a0, where an, an-1, …, a1, a0 are constants, and n is a non-negative integer.
Rational functions, on the other hand, are ratios of two polynomial expressions. They can be written as f(x) = p(x)/q(x), where p(x) and q(x) are polynomials, and q(x) is not equal to zero.
One important property of polynomials is that they can have different degrees, which is determined by the highest power of the variable in the expression. For example, a polynomial with the highest power of x being 2 is called a quadratic function, while a polynomial with the highest power of x being 3 is called a cubic function.
Rational functions, on the other hand, can have vertical asymptotes and holes in their graphs due to the restrictions on the denominator. Vertical asymptotes occur where the denominator of the rational function equals zero, and the function approaches positive or negative infinity. Holes occur when both the numerator and denominator have a factor that cancels out.
Overall, understanding polynomials and rational functions is crucial for solving equations, graphing functions, and analyzing mathematical models in various fields of study. By mastering these concepts, individuals can more effectively tackle complex problems and gain a deeper understanding of the mathematical world.
What are Polynomials?
A polynomial is a mathematical expression that consists of variables, coefficients, and exponents. It is a sum of one or more terms, where each term is a variable raised to a non-negative integer power, multiplied by a coefficient.
Polynomials are often used in algebra and calculus to model various real-life phenomena, such as population growth, financial investments, and physical processes. They are also used to solve equations and find mathematical solutions.
A polynomial can be classified by the highest power of the variable. For example, a polynomial with a highest power of 2 is called a quadratic polynomial, while a polynomial with a highest power of 3 is called a cubic polynomial.
Polynomials can be added, subtracted, multiplied, and divided, just like numbers. They can also be factored to find their roots, or solutions. The roots of a polynomial are the values of the variable that make the polynomial equal to zero.
In summary, polynomials are mathematical expressions that consist of variables, coefficients, and exponents. They are used to model real-life phenomena, solve equations, and find mathematical solutions.
Characteristics of Polynomials
A polynomial function is a mathematical expression that is made up of one or more terms, where each term consists of a coefficient multiplied by a variable raised to a non-negative integer exponent. The highest exponent in the polynomial is called the degree of the polynomial. Polynomials are widely used in various fields of mathematics and sciences due to their simplicity and versatility.
One of the key characteristics of polynomials is that they are continuous functions. This means that there are no breaks or gaps in the graph of a polynomial function. The graph of a polynomial can be drawn without lifting the pen from the paper. This property makes polynomials very useful in modeling real-world phenomena, as they can accurately represent continuous relationships between variables.
Another important characteristic of polynomials is that they can have multiple roots or zeros. A root of a polynomial is a value of the variable that makes the polynomial equal to zero. The number of roots of a polynomial is equal to its degree, although some roots may be repeated. The roots of a polynomial can provide valuable information about the behavior of the function and can be used to solve equations involving the polynomial.
In addition to being continuous and having multiple roots, polynomials also have specific end behavior. The end behavior of a polynomial function is determined by the leading term, which is the term with the highest degree. If the leading term has a positive coefficient and an even degree, the graph of the polynomial will have both ends pointing upwards. If the leading term has a positive coefficient and an odd degree, the graph will have one end pointing upwards and the other end pointing downwards. Conversely, if the leading term has a negative coefficient, the end behavior will be the opposite.
In conclusion, polynomials are mathematical expressions that have several important characteristics. They are continuous functions, can have multiple roots, and exhibit specific end behavior based on the leading term. Understanding these characteristics can help in analyzing and interpreting polynomial functions and their graphs.
Polynomial Functions
Polynomial functions are algebraic expressions that contain one or more terms, each of which is a variable raised to a non-negative integer exponent and multiplied by a constant coefficient. These functions can be written in the general form:
f(x) = anxn + an-1xn-1 + … + a1x + a0
Here, an, an-1, …, a1, a0 are constants, and n is a non-negative integer representing the degree of the polynomial function. The degree of a polynomial is the highest power of the variable in the expression.
Polynomial functions can have various shapes and characteristics depending on their degree and coefficients. They can be classified as linear (degree 1), quadratic (degree 2), cubic (degree 3), and so on. These functions can be graphed to visualize their behavior and understand their properties.
The fundamental operations of arithmetic, such as addition, subtraction, multiplication, and division, are applicable to polynomial functions. By performing these operations on polynomial functions, we can manipulate and simplify their expressions, solve equations involving polynomials, and analyze their behavior and characteristics.
Analyzing Rational Functions

A rational function is a function that can be expressed as the quotient of two polynomial functions. This type of function often appears in mathematics and physics to model various real-world phenomena. Analyzing rational functions involves understanding their behavior, determining key points, and identifying important features.
One of the first steps in analyzing a rational function is finding its domain. The domain is the set of all possible input values for which the function is defined. In a rational function, the denominator must not be equal to zero, as division by zero is undefined. Therefore, the domain of a rational function is all real numbers except the values that make the denominator zero.
The next step is to locate the vertical asymptotes. These are vertical lines that the graph approaches but never touches. Vertical asymptotes occur when the denominator of a rational function equals zero, but the numerator does not. To find the vertical asymptotes, set the denominator equal to zero and solve for the variable.
The horizontal asymptotes can also be determined. These are horizontal lines that the graph approaches as the input values become very large or very small. To find the horizontal asymptotes of a rational function, compare the degrees of the numerator and denominator. If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0. If the degrees are equal, the horizontal asymptote is the ratio of the leading coefficients. If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
Additional features of rational functions include x-intercepts and y-intercepts. The x-intercepts occur when the numerator of the rational function equals zero. The y-intercept is the value of the function when x = 0. These points can be found by setting the respective variables equal to zero and solving for the other variable.
In summary, analyzing rational functions involves determining the domain, locating vertical and horizontal asymptotes, finding x-intercepts and y-intercepts, and analyzing other features of the function. This process allows for a better understanding of the behavior and characteristics of the function.
Identifying Key Features of Rational Functions
When studying rational functions, it is important to be able to identify key features that can help us understand the behavior of the function. These features include the vertical and horizontal asymptotes, the x- and y-intercepts, and any holes in the graph. By analyzing these features, we can gain insight into the overall shape and behavior of the function.
Vertical asymptotes: A vertical asymptote is a vertical line that the graph of the function approaches but never touches. It occurs where the denominator of the rational function equals zero. To find vertical asymptotes, we set the denominator equal to zero and solve for x. The vertical asymptote helps us understand the behavior of the function as x approaches positive or negative infinity.
Horizontal asymptotes: A horizontal asymptote is a horizontal line that the graph of the function approaches as x approaches positive or negative infinity. It can be found by analyzing the degrees of the numerator and denominator of the rational function. If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0. If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is the ratio of the leading coefficients. If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
X-intercepts: The x-intercepts of a rational function are the values of x for which the function equals zero. To find the x-intercepts, we set the numerator of the rational function equal to zero and solve for x.
Y-intercept: The y-intercept of a rational function is the value of y when x is zero. To find the y-intercept, we substitute x = 0 into the rational function and solve for y.
Holes: Holes in the graph of a rational function occur when there is a common factor between the numerator and denominator that can be canceled out. To find the location of the hole, we set the common factor equal to zero and solve for x. The hole can then be plotted on the graph as an open circle.
By identifying and analyzing these key features, we can have a better understanding of the behavior and characteristics of a rational function. These features allow us to make predictions about the graph and to solve problems involving rational functions.
Answer Key for Chapter 2 Polynomial and Rational Functions
In this article, we provided the answer key for Chapter 2 of the Polynomial and Rational Functions subject. This chapter covers various topics related to polynomials and rational functions, including finding zeros, long division, synthetic division, and graphing functions.
The answer key includes step-by-step solutions and explanations for all the problems in Chapter 2. It serves as a helpful resource for students to check their answers, understand the concepts better, and improve their problem-solving skills.
The chapter covers important concepts in the study of Polynomial and Rational Functions, which are essential for further studies in mathematics. By providing the answer key, we aim to assist students in their learning process and help them succeed in their studies.
We hope that this answer key for Chapter 2 Polynomial and Rational Functions proves to be a valuable resource for students and helps them excel in their studies. Studying polynomials and rational functions can be challenging, but with the right resources and practice, students can develop a strong understanding of the subject.