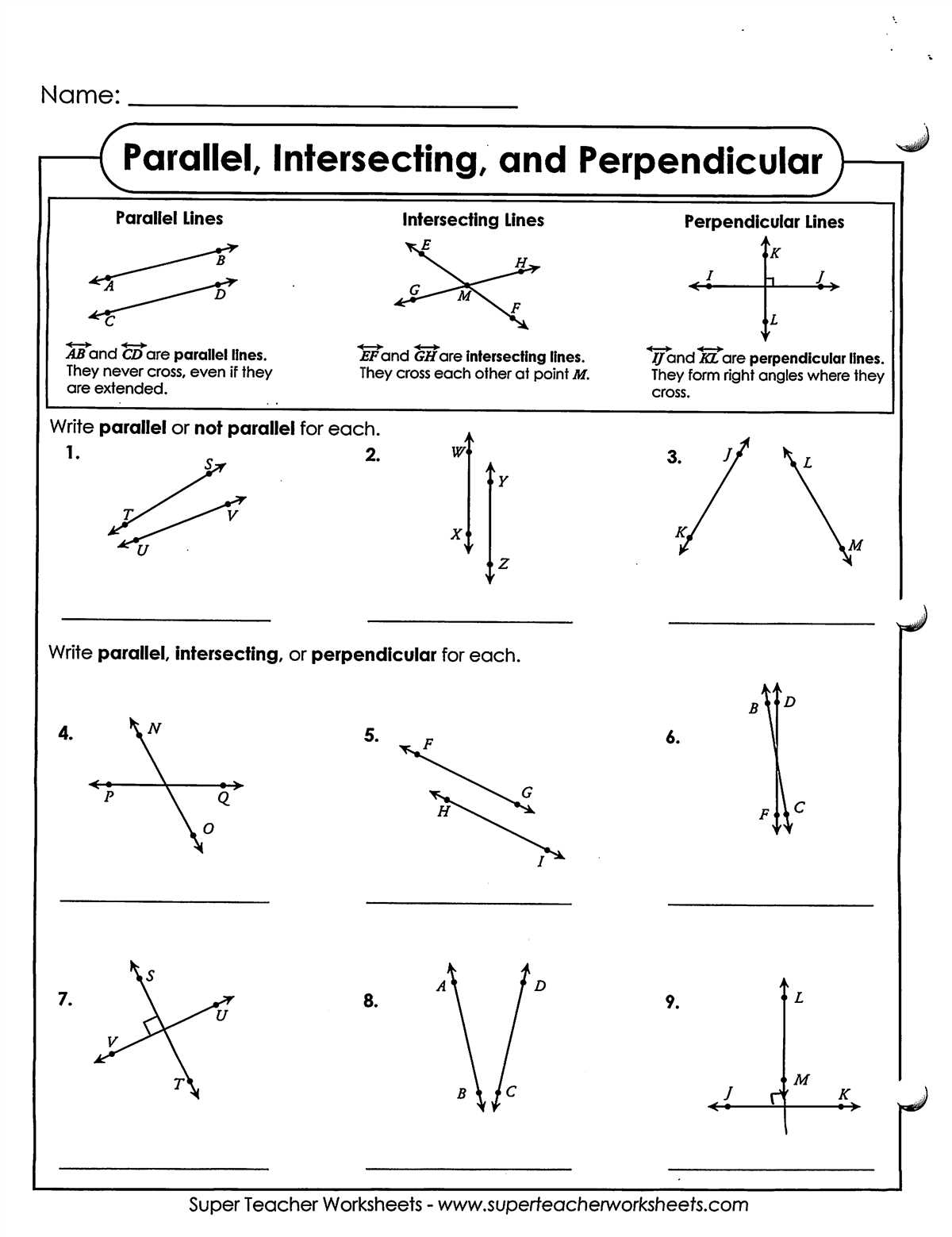
In Chapter 3 of the textbook, we explore the fascinating world of parallel and perpendicular lines. These types of lines play a crucial role in various mathematical concepts and applications. Understanding their properties and relationships is essential for solving problems involving angles, slopes, and intersecting lines.
The chapter begins with an introduction to the basic definitions of parallel and perpendicular lines. We learn that parallel lines are lines that never intersect and have the same slope, while perpendicular lines are lines that intersect at a right angle and have slopes that are negative reciprocals of each other.
Throughout the chapter, we encounter various theorems and postulates that help us identify and prove parallel and perpendicular lines. These include the Alternate Interior Angles Theorem, Converse of the Corresponding Angles Postulate, and the Perpendicular Transversal Theorem. By applying these concepts and theorems, we can solve problems involving parallel and perpendicular lines, such as finding missing angles or proving geometric relationships.
By the end of Chapter 3, we will have a solid understanding of parallel and perpendicular lines and their properties. We will be able to confidently identify and work with these types of lines in various mathematical contexts. So let’s dive in and explore the fascinating world of parallel and perpendicular lines!
Chapter 3 Parallel and Perpendicular Lines Answers
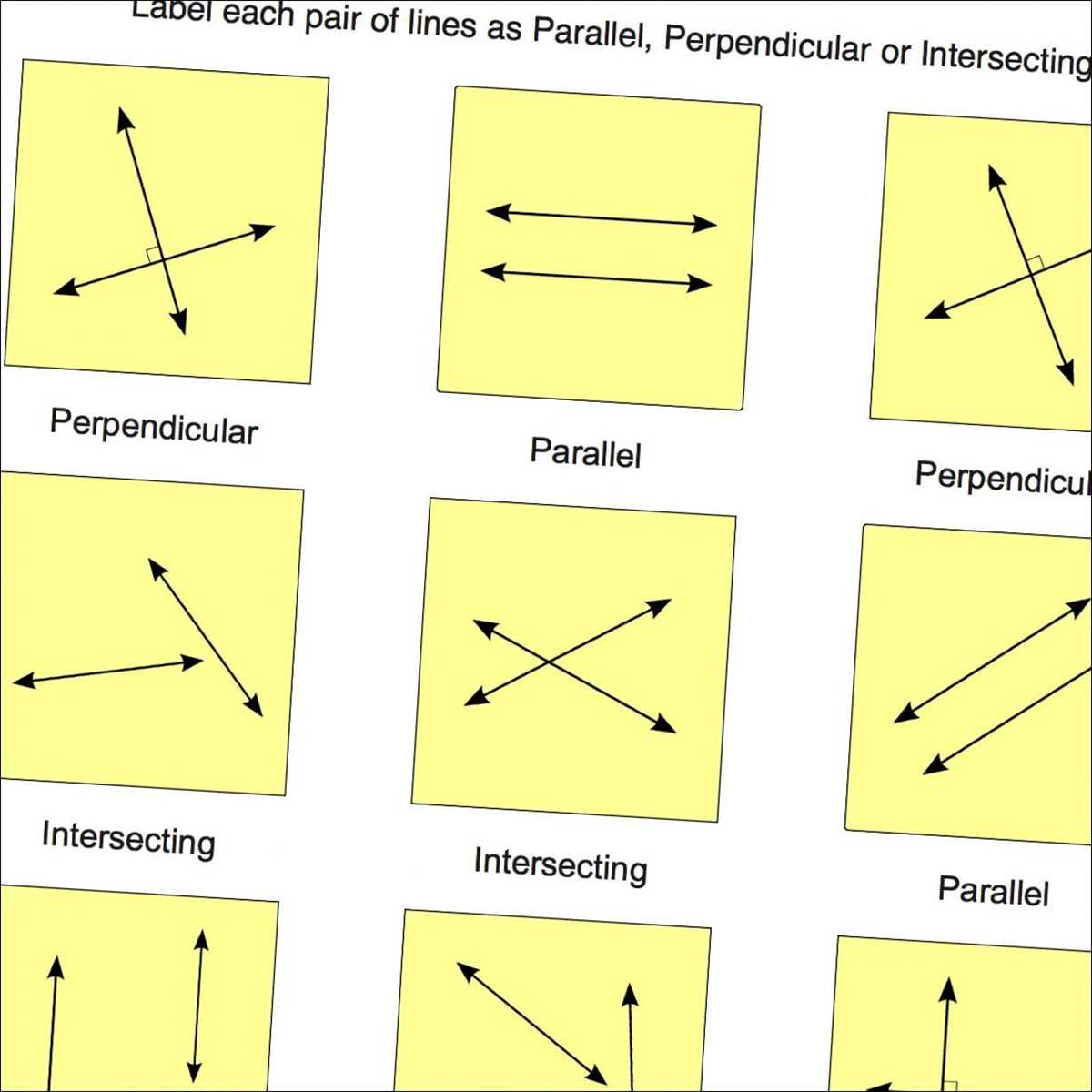
In Chapter 3 of our math textbook, we explored the topic of parallel and perpendicular lines. This chapter focused on understanding the properties and relationships of these types of lines, as well as solving problems involving parallel and perpendicular lines.
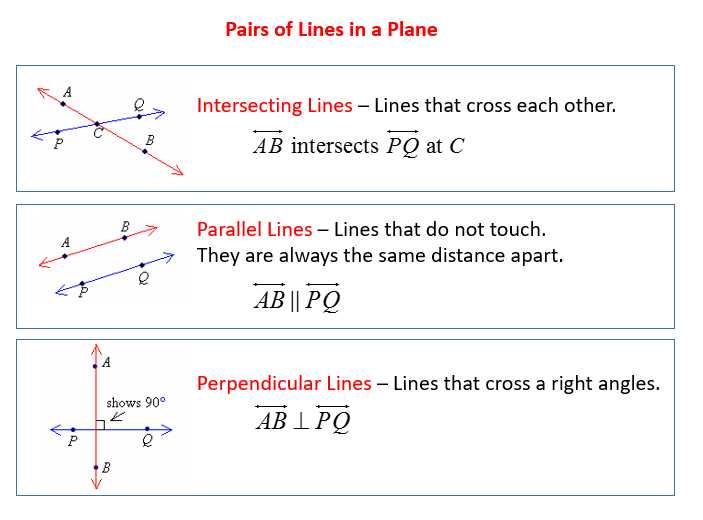
One of the key concepts covered in this chapter was the definition of parallel lines. We learned that parallel lines are two or more lines that are always the same distance apart and never intersect. We also learned that parallel lines have the same slope.
To determine if two lines are parallel, we can compare their slopes. If the slopes are equal, then the lines are parallel. If the slopes are not equal, then the lines are not parallel. This concept was reinforced through various practice problems and exercises.
In addition to parallel lines, we also discussed perpendicular lines in this chapter. Perpendicular lines are two lines that intersect at a 90 degree angle. The slopes of perpendicular lines are negative reciprocals of each other, meaning if one slope is m1, the slope of the perpendicular line is -1/m1.
We practiced finding equations of lines that are parallel or perpendicular to a given line, as well as finding the slopes of lines that are parallel or perpendicular to a given line. These skills are essential when solving real-world problems that involve parallel and perpendicular lines.
In conclusion, Chapter 3 provided us with a solid foundation in understanding and working with parallel and perpendicular lines. Through various examples, explanations, and exercises, we developed the necessary skills to identify, compare, and work with parallel and perpendicular lines. This knowledge will be helpful in future chapters and in real-life applications that involve geometric concepts.
Understanding Parallel Lines
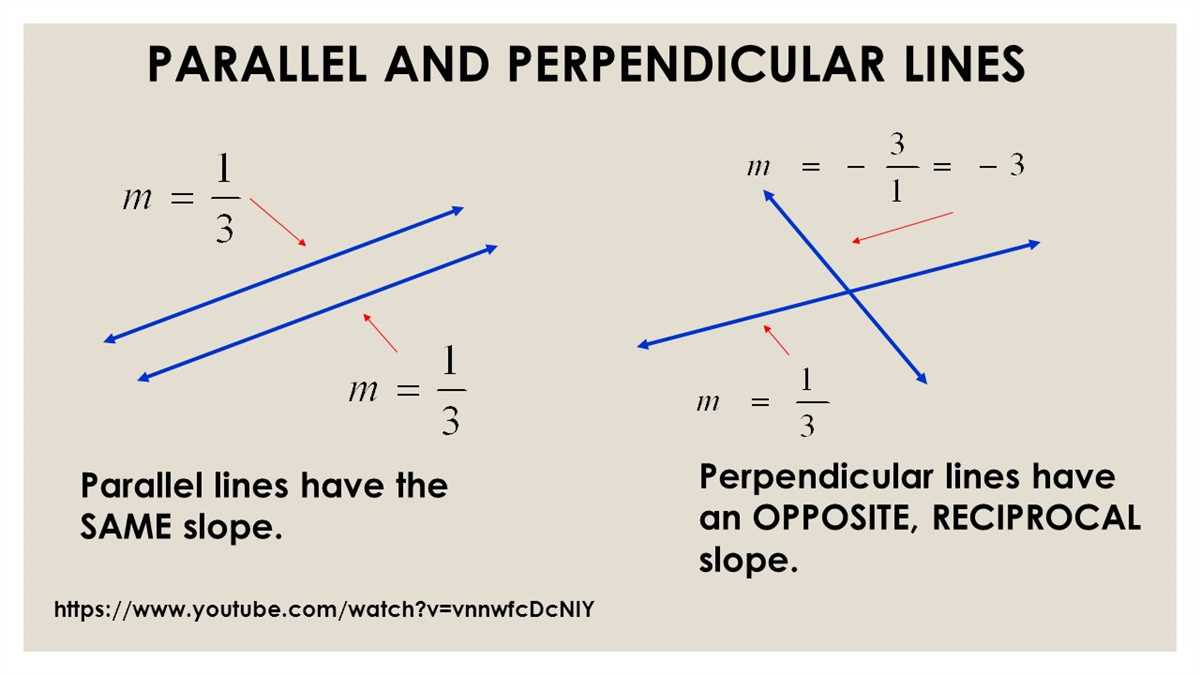
Parallel lines are a fundamental concept in geometry, and understanding them is crucial for solving various mathematical problems. Two lines are said to be parallel if they never intersect each other, no matter how far they are extended. This concept is denoted by a symbol consisting of two vertical lines, known as a parallel symbol.
One important characteristic of parallel lines is that they have the same slope. In other words, the steepness or inclination of the lines is equal. This property allows us to determine if two lines are parallel by comparing their slopes. If the slopes are the same, the lines are parallel; otherwise, they intersect at some point.
Parallel lines also have several properties that can help us solve geometry problems. For example, parallel lines create congruent alternate interior angles, congruent corresponding angles, and congruent exterior angles. These properties can be used to prove theorems and solve problems involving angles and lines.
- Alternate interior angles are the pair of angles formed between two lines and on opposite sides of a transversal. They are congruent when the lines are parallel.
- Corresponding angles are the pair of angles formed when a transversal intersects two parallel lines. They are congruent.
- Exterior angles are the angles formed by one side of a triangle and the extension of another side. They are congruent when the lines are parallel.
Understanding parallel lines and their properties is essential for solving various geometric problems and proofs. It allows us to identify parallel lines, determine angle relationships, and apply them to solve real-world problems.
| Property | Description |
|---|---|
| Parallel Lines | Two lines that never intersect and have the same slope. |
| Alternate Interior Angles | Pair of congruent angles formed between two lines and on opposite sides of a transversal. |
| Corresponding Angles | Pair of congruent angles formed when a transversal intersects two parallel lines. |
| Exterior Angles | Angles formed by one side of a triangle and the extension of another side. |
Proving Lines are Parallel
In geometry, parallel lines are lines that never intersect. Proving that two lines are parallel can be done using a variety of methods. One common method is the use of alternate interior angles. If the alternate interior angles formed by two lines and a transversal are congruent, then the lines are parallel. This can be proven using the corresponding angles postulate or the alternate interior angles theorem.
Another method for proving lines are parallel is through the use of the same-side interior angles. If the same-side interior angles formed by two lines and a transversal are supplementary, then the lines are parallel. This can be proven using the same-side interior angles theorem.
Additionally, the slopes of two lines can be used to determine if they are parallel. If two lines have the same slope, then they are parallel. This can be proven using the slope-intercept form of a linear equation and comparing the slopes.
Proving that lines are parallel is an important concept in geometry and can be used to solve various real-world problems. It allows us to understand and analyze the relationships between different lines and angles, and provides a foundation for further geometric proofs and theorems.
Finding Equations of Parallel Lines
When working with parallel lines, it is important to understand that they have the same slope. This means that if we have the equation of one line, we can easily find the equation of another line that is parallel to it.
To find the equation of a parallel line, we need two pieces of information: the slope of the given line and a point that lies on the parallel line. Once we have this information, we can use the point-slope form of a line to write the equation.
The point-slope form of a line is given by the equation y − y₁ = m(x − x₁), where (x₁, y₁) is a point on the line and m is the slope of the line. By substituting the known values of the slope and point into this equation, we can find the equation of the parallel line.
For example, consider the line with equation y = 2x + 3. We know that any line parallel to this line will also have a slope of 2. Suppose we want to find the equation of a line parallel to this line that passes through the point (4, 5). Using the point-slope form, we can write the equation as y − 5 = 2(x − 4).
Simplifying this equation will give us the final equation of the parallel line. In this case, we have y − 5 = 2x − 8, which can be rearranged to y = 2x − 3. Therefore, the equation of the parallel line passing through the point (4, 5) is y = 2x − 3.
By understanding the concept of parallel lines and how to find their equations, we can solve various geometry and algebra problems that involve parallel lines.
Understanding Perpendicular Lines
Perpendicular lines are an important concept in geometry and have several defining characteristics. To understand perpendicular lines, we must first define what a line is. A line is a straight path that extends infinitely in both directions. It has no thickness and is made up of an infinite number of points.
In geometry, perpendicular lines are two lines that intersect at a right angle, or 90 degrees. This means that the lines form a “T” shape when they intersect. The point of intersection is called the point of perpendicularity. Perpendicular lines have a unique property – the slopes of these lines are negative reciprocals of each other. In other words, if the slope of one line is m, then the slope of the other line is -1/m.
Key characteristics of perpendicular lines:
- They intersect at a right angle (90 degrees).
- The slopes of the lines are negative reciprocals of each other.
- They create a “T” shape at the point of intersection.
Perpendicular lines are commonly seen in many real-life situations, such as the corners of buildings, the intersecting lines on a sheet of graph paper, or the “L” shape of a ruler. They also play an important role in various mathematical concepts, including the calculation of slope and the construction of right angles.
Proving Lines are Perpendicular
The concept of perpendicular lines is an important one in geometry. Perpendicular lines intersect at a 90-degree angle, creating a right angle. Proving that two lines are perpendicular involves demonstrating that the corresponding angles formed by the intersecting lines are congruent, and that the adjacent angles are supplementary.
One method for proving that lines are perpendicular is by using the slope-intercept form of a line. This form is written as y = mx + b, where m represents the slope of the line. If two lines have slopes that are negative reciprocals of each other, then they are perpendicular. This can be proven by multiplying the slopes together. If the product is -1, then the lines are perpendicular.
Another method for proving perpendicularity is by using the Pythagorean theorem. If two lines intersect to form a right angle, the lengths of the segments created by the intersection can be compared using the Pythagorean theorem. If the squares of the lengths of the two shorter segments add up to the square of the length of the longer segment, then the lines are perpendicular.
Overall, proving that lines are perpendicular can be accomplished through various methods, including comparing slopes and using the Pythagorean theorem. These techniques allow us to determine the relationship between lines in a geometric context and provide a basis for further analysis and problem-solving.
Finding Equations of Perpendicular Lines
In this chapter, we have explored the concepts of parallel and perpendicular lines and how to determine their equations. Specifically, we have learned that the slopes of parallel lines are equal, while the slopes of perpendicular lines are negative reciprocals of each other.
When given a line and a point, we can use these concepts to find the equation of the perpendicular line. To do this, we need to determine the slope of the given line and then find the negative reciprocal of that slope. We can then use this new slope and the given point to write the equation of the perpendicular line in point-slope form.
To summarize, when finding the equation of a perpendicular line:
- Determine the slope of the given line.
- Find the negative reciprocal of that slope.
- Use the negative reciprocal slope and the given point to write the equation of the perpendicular line in point-slope form.
By understanding the relationship between parallel and perpendicular lines and knowing how to find their equations, we can solve various geometry and algebraic problems. These skills are valuable in fields such as architecture, engineering, and physics, where parallel and perpendicular lines frequently appear in design and measurement.