
This section focuses on the essential principles and techniques required to solve problems that test your knowledge of specific mathematical topics. It is crucial to grasp the underlying methods and formulas, which serve as the foundation for resolving various types of questions. Mastery of these concepts will help improve performance on any related assessments.
Important Formulas and Theorems

To excel in solving problems, you must familiarize yourself with the key formulas and theorems related to the material. These tools serve as the backbone for most questions and guide you towards accurate solutions. A few of the most important include:
- Area and Perimeter Formulas: Understanding the basic measurements of geometric shapes is essential.
- Angle Relationships: Recognizing how angles interact with each other is fundamental to solving many problems.
- Proportions and Ratios: These are often used in scaling problems or when comparing different figures.
Common Mistakes to Avoid
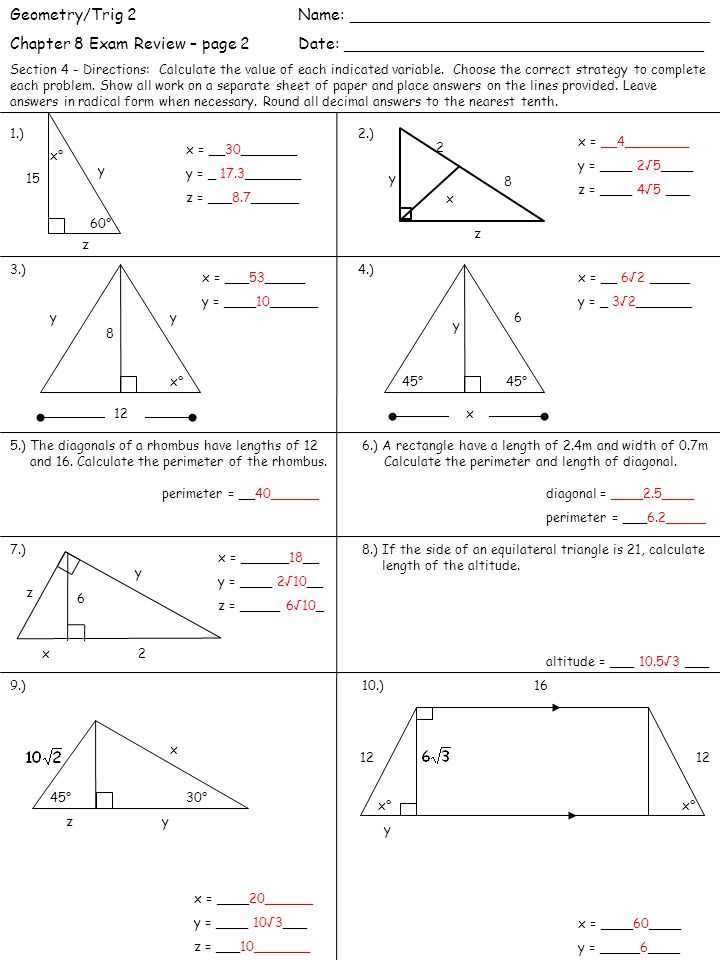
Many students face challenges when trying to apply their knowledge under pressure. Some of the most common errors include:
- Failing to correctly identify the shape or figure in question.
- Misapplying formulas due to overlooking specific conditions or constraints.
- Rushing through the calculation process and missing critical steps.
Step-by-Step Problem Solving
Breaking down each problem into manageable steps is key to ensuring you arrive at the correct conclusion. Here’s an approach to follow:
- Read the problem carefully: Understand what is being asked before proceeding with any calculations.
- Identify known values: Mark the information given in the problem that can help you apply the correct formulas.
- Apply relevant formulas: Use the correct mathematical principles to calculate the solution.
- Review your work: Double-check calculations and ensure that all steps are logical and well-executed.
Strategies for Improvement

To enhance your skills and perform better on related evaluations, consistent practice is key. Consider the following strategies:
- Work through a variety of practice problems regularly.
- Review your mistakes and understand where errors were made.
- Seek additional resources such as online tutorials or practice guides to reinforce your knowledge.
With time, dedication, and a solid understanding of the principles, you will be well-equipped to tackle any challenges that come your way.
Mastering Problems in Mathematics
Effective Strategies for Assessments
Key Theorems Every Student Should Know
Common Mistakes in Assessments
Improving Test-Taking Techniques
Step-by-Step Solutions for Problems
Enhancing Performance on Exams
In this section, we explore the essential techniques for tackling mathematical problems efficiently. Understanding fundamental principles and honing your problem-solving approach can significantly improve your results. By mastering key concepts and recognizing common pitfalls, students can approach any given challenge with confidence and precision.
Effective strategies for approaching assessments involve not just memorizing formulas but also developing a deep understanding of the material. Breaking down complex questions into smaller, more manageable tasks allows for a clearer and faster solution. It’s important to focus on learning the steps required for each type of problem rather than relying solely on quick fixes.
Every student should be familiar with critical theorems that serve as the foundation for most problems. These theorems help students draw correct conclusions and identify solutions more efficiently. For example, the properties of triangles, circles, and polygons are frequently used to solve a variety of challenges in this field.
Common mistakes often arise when students rush through problems or fail to grasp the underlying principles. Misinterpretation of a figure, incorrect application of theorems, and simple arithmetic errors can lead to avoidable mistakes. It’s crucial to carefully read each question and check all steps before finalizing an answer.
Improving test-taking techniques involves developing strategies for time management and focusing on accuracy. Allocate enough time to each section, leaving room for review at the end. If you get stuck, move on to the next problem and return later with a fresh perspective.
Using step-by-step solutions for various problems allows for a more structured approach. First, identify the known information, then apply the relevant principles, and finally check your results. This method ensures that no steps are skipped and leads to more accurate results in a consistent manner.
Ultimately, enhancing performance on exams requires consistent practice, review, and a strong understanding of the material. Regular practice, careful error analysis, and mastery of essential concepts are key to excelling in any mathematical challenge.