
Welcome to our comprehensive review of Chapter 6 in Geometry! In this article, we will go over the answers to the test questions that cover a range of topics, including polygons, triangles, angles, and circles. Whether you are a student preparing for an upcoming test or a teacher looking for a resource to help your students review, this article will provide you with the answers you need.
Chapter 6 in Geometry is a crucial section that delves into the properties and characteristics of various geometric shapes. Understanding these concepts is essential as they form the foundation for more complex topics in geometry. By going through the test questions and their corresponding answers, you will gain a clearer understanding of the content covered in this chapter and be better prepared for any assessments that may come your way.
In this article, we will break down each test question and provide a detailed explanation of the answer. We will also offer tips and strategies for solving these types of problems. Additionally, we will include examples and diagrams to aid in your understanding. By the end of this article, you will have a solid grasp of the concepts covered in Chapter 6 and feel confident in your ability to tackle any geometry test.
Chapter 6 Test Review Geometry Answers
In this review, we will go over the answers to the questions on the Chapter 6 test in geometry. It is important to understand these concepts in order to succeed on the test and have a solid foundation in geometry.
1. Question: Find the missing angle in the triangle. The two given angles are 40 degrees and 90 degrees.
Answer: To find the missing angle, we need to subtract the sum of the two given angles from 180 degrees. Therefore, the missing angle is 50 degrees.
2. Question: Determine whether the two given lines are parallel. Line 1 has a slope of 2 and a y-intercept of 3, while Line 2 has a slope of -2 and a y-intercept of 6.
Answer: To determine if two lines are parallel, we need to check if their slopes are equal. In this case, the slopes are not equal (2 and -2), so the lines are not parallel.
3. Question: Find the perimeter of a rectangle with length 10 cm and width 6 cm.
Answer: The perimeter of a rectangle is found by adding the lengths of all its sides. In this case, the perimeter is 2(10 cm) + 2(6 cm) = 20 cm + 12 cm = 32 cm.
4. Question: Determine the area of a circle with a radius of 5 cm.
Answer: The formula to calculate the area of a circle is A = πr², where A is the area and r is the radius. Plugging in the given radius, we get A = π(5 cm)² = π(25 cm²) = 25π cm².
5. Question: Find the volume of a rectangular prism with length 8 cm, width 4 cm, and height 6 cm.
Answer: The volume of a rectangular prism is found by multiplying its length, width, and height. In this case, the volume is 8 cm * 4 cm * 6 cm = 192 cm³.
These are just a few examples of the types of questions that may be on the Chapter 6 geometry test. It is important to review all of the concepts covered in the chapter and practice solving similar problems to ensure success on the test.
Overview
In Chapter 6 of the geometry course, students will be reviewing concepts and skills related to various topics. This chapter serves as a comprehensive test review, allowing students to reinforce their understanding and practice problem-solving techniques. The topics covered in this chapter include angles, triangles, quadrilaterals, circles, and transformations.
Students will start by reviewing angle relationships, such as complementary, supplementary, vertical, and adjacent angles. They will also study the properties and relationships of triangles, including the classification of triangles based on their side lengths and angles. The chapter will also cover the properties and classification of quadrilaterals, such as parallelograms, rectangles, squares, and trapezoids.
Furthermore, students will learn about the properties of circles, including the relationship between the radius, diameter, and circumference. They will also study angles formed by chords, secants, and tangents in circles. Finally, the chapter will conclude with a review of transformations, including translations, reflections, rotations, and dilations, and how these transformations affect geometric figures.
This chapter provides students with the opportunity to review and practice important concepts and skills that will be assessed in the upcoming Chapter 6 test. By reviewing these topics thoroughly, students can strengthen their understanding and improve their problem-solving abilities in geometry.
Understanding the Basic Concepts

In geometry, understanding the basic concepts is crucial for further learning and problem-solving. These concepts serve as the foundation for understanding more complex topics and solving geometric problems. Here are some key concepts that are fundamental to geometry:
Points
A point is a specific location in space that has no size or shape. It is represented by a dot and is often labeled with a capital letter. Points are used to define and describe other geometric figures.
Lines
A line is a straight path that extends infinitely in both directions. It is represented by a straight line with arrows on both ends or by using two points labeled with capital letters. Lines can be used to describe the position and direction of other geometric figures.
Angles
An angle is formed when two rays share a common endpoint. It is measured in degrees and is often labeled with a letter or a number. Angles are used to describe the amount of rotation or the opening between two intersecting lines or line segments.
These are just a few basic concepts in geometry. They provide a starting point for understanding more complex topics such as polygons, triangles, and circles. By mastering these foundational concepts, students can develop strong problem-solving skills and approach more challenging geometry problems with confidence.
Working with Angles and Lines
Angles and lines are fundamental concepts in geometry. They play a crucial role in understanding the relationships between different shapes and figures. By studying angles and lines, we can analyze and solve a wide range of geometric problems.
Angles: An angle is formed when two rays share a common endpoint, called the vertex. The size of an angle is measured in degrees, with a full circle measuring 360 degrees. There are several types of angles, including acute angles (less than 90 degrees), right angles (exactly 90 degrees), obtuse angles (more than 90 degrees but less than 180 degrees), and straight angles (exactly 180 degrees).
Lines: In geometry, a line is an infinitely long, straight path that extends in both directions. It is made up of an infinite number of points. Lines are characterized by their slope and y-intercept in the coordinate plane. Horizontal lines have a slope of 0, while vertical lines have an undefined slope.
When working with angles and lines, there are several important concepts to consider. These include angle relationships such as vertical angles (opposite angles formed by intersecting lines), supplementary angles (two angles that add up to 180 degrees), and complementary angles (two angles that add up to 90 degrees). Additionally, parallel lines (lines that never intersect) and perpendicular lines (lines that intersect at a 90-degree angle) play a significant role in geometric proofs and constructions.
Understanding angles and lines is essential not only in geometry but also in various real-world applications. Architects, engineers, and designers rely on these concepts when creating and analyzing structures. Moreover, angles and lines are used in navigation, map reading, and trigonometry, making them valuable tools in everyday life.
Exploring Geometric Figures
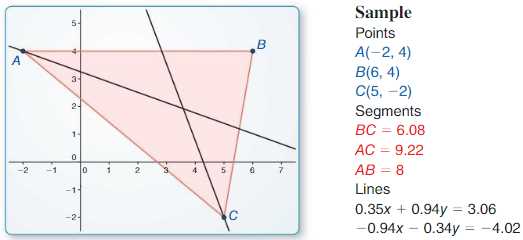
Geometry is the branch of mathematics that deals with shapes, sizes, and properties of geometric figures. Exploring geometric figures is an essential part of learning geometry as it helps us understand the characteristics and relationships of various shapes.
One of the fundamental concepts in geometry is the classification of geometric figures. Geometric figures can be classified into two-dimensional (2D) and three-dimensional (3D) shapes. Some examples of 2D shapes include triangles, squares, and circles, while examples of 3D shapes are cubes, spheres, and pyramids.
In geometry, we study different properties of geometric figures. For example, we learn about the angles of triangles, the lengths of sides in polygons, and the formulas to calculate the areas and volumes of various shapes. These properties help us analyze and solve problems related to geometric figures.
Another aspect of exploring geometric figures is understanding their relationships. For instance, we can identify congruent figures, which have the same shape and size, or similar figures, which have the same shape but different sizes. These relationships help us make connections between different geometric figures and apply them to solve more complex problems.
Furthermore, exploring geometric figures involves investigating symmetry, transformations, and coordinate geometry. Symmetry refers to the balance and reflection of shapes, while transformations involve translating, rotating, and reflecting figures. Coordinate geometry uses coordinates and equations to represent and analyze geometric figures on a coordinate plane.
Overall, exploring geometric figures is an exciting journey that allows us to delve into the fascinating world of shapes and their properties. By studying and understanding geometric figures, we can develop critical thinking skills, problem-solving abilities, and a deeper appreciation for the beauty and orderliness of mathematics.
Applying Formulas and Equations
Geometry involves the study of shapes and their properties. One important aspect of geometry is the use and application of formulas and equations. These tools allow us to calculate various measurements and solve problems related to angles, lengths, and areas.
When working with formulas and equations in geometry, it is important to understand the properties and relationships of different shapes. For example, the formula for finding the area of a rectangle is A = length × width, while the formula for finding the area of a triangle is A = ½ base × height. By knowing these formulas, we can easily calculate the area of these shapes.
Equations are also useful in geometry, particularly when solving for unknown angles or lengths. For instance, when dealing with right triangles, we can use the Pythagorean theorem (a² + b² = c²) to find the length of the hypotenuse or one of the legs. Equations can also be used to solve for missing angles in polygons, such as the sum of the angles in a triangle (180 degrees) or the sum of the angles in a quadrilateral (360 degrees).
Key Formulas and Equations:
- Area of a rectangle: A = length × width
- Area of a triangle: A = ½ base × height
- Pythagorean theorem: a² + b² = c²
- Sum of angles in a triangle: 180 degrees
- Sum of angles in a quadrilateral: 360 degrees
By understanding and applying these formulas and equations, we can effectively solve geometry problems and calculate various measurements. Practice and familiarity with these tools will enable us to navigate the complexities of geometry with confidence.
Practice Problems and Solutions
In this section, you will find a set of practice problems related to the topics covered in Chapter 6 of geometry. Each problem is followed by a detailed solution to help you understand how to approach and solve similar problems.
Problem 1:
Find the area of a triangle with base 5 cm and height 8 cm.
Solution:
Using the formula for the area of a triangle, we have:
Area = (1/2) * base * height
Substituting the given values, we get:
Area = (1/2) * 5 cm * 8 cm = 20 cm²
Problem 2:
Find the perimeter of a rectangle with length 10 cm and width 6 cm.
Solution:
The formula for the perimeter of a rectangle is given by:
Perimeter = 2 * (length + width)
Substituting the given values, we get:
Perimeter = 2 * (10 cm + 6 cm) = 32 cm
Problem 3:

Find the volume of a sphere with radius 5 cm.
Solution:
The formula for the volume of a sphere is given by:
Volume = (4/3) * pi * radius³
Substituting the given value and using the approximation of pi as 3.14, we get:
Volume = (4/3) * 3.14 * 5 cm³ ≈ 523.33 cm³
These practice problems and solutions cover some of the key concepts discussed in Chapter 6 of geometry. By working through these problems, you can reinforce your understanding of the material and improve your problem-solving skills. Remember to review the relevant formulas and concepts before attempting the problems, and check your answers using the provided solutions.