When it comes to solving piecewise functions, circuit training can be a helpful tool. Circuit training is a method of practice that involves moving from one station to another, solving different problems at each station. This approach allows students to gain confidence and fluency in solving a variety of problems, including those involving piecewise functions.
Piecewise functions are functions that are defined by different formulas on different intervals. They are typically represented graphically as a combination of several lines or curves. Solving piecewise functions involves determining the correct formula to use on each interval and finding the corresponding values.
By using circuit training to practice solving piecewise functions, students can develop a deeper understanding of the concept and improve their problem-solving skills. Circuit training allows for active engagement and repetition, which are key components of effective learning. It also provides immediate feedback, as students can check their answers at each station, allowing them to identify and correct any mistakes.
Circuit Training Piecewise Functions Answers
When it comes to circuit training piecewise functions, it is important to have the correct answers to ensure that you are getting the most out of your workout. Piecewise functions involve breaking a function into different intervals or “pieces” and applying a different rule to each interval. This type of training can be challenging but also provides a great opportunity for targeting different muscle groups and improving overall fitness.
One of the key answers when working with circuit training piecewise functions is understanding the rules that govern each interval. Each interval may have a different equation or set of conditions that need to be met. By carefully analyzing the function and its intervals, you can determine the appropriate rules and ensure that you are performing each exercise correctly.
Another important answer when working with circuit training piecewise functions is knowing how to transition between intervals. This is crucial to maintaining the flow and intensity of your workout. It is important to smoothly move from one exercise to the next, ensuring that you are challenging your muscles while also preventing injury. Having a solid understanding of the piecewise function and its intervals will help you to make these transitions effectively.
Overall, having the correct answers when working with circuit training piecewise functions is essential for a successful and effective workout. By understanding the rules for each interval and knowing how to transition between intervals, you can maximize your results and improve your overall fitness.
What Are Piecewise Functions?
A piecewise function is a mathematical function that is defined by different rules or formulas for different parts or intervals of its domain. It is also known as a piecewise-defined function or a hybrid function. This type of function is often used to model real-life situations that involve different conditions or scenarios.
In a piecewise function, the domain is divided into several intervals or sections, and a different formula or rule is applied to each interval. These formulas or rules are typically defined using different mathematical expressions or equations. The function’s value depends on which interval the input value falls into, and the corresponding formula or rule is used to calculate the output value.
For example, consider a piecewise function that represents the cost of a taxi ride based on the distance traveled:
- For distances less than or equal to 5 kilometers, the cost is $5.
- For distances greater than 5 kilometers but less than or equal to 10 kilometers, the cost is $10.
- For distances greater than 10 kilometers, the cost is $10 plus $2 for each additional kilometer.
In this example, the piecewise function can be defined as:
f(x) = $5 if x ≤ 5
f(x) = $10 if 5 < x ≤ 10
f(x) = $10 + $2(x - 10) if x > 10
Piecewise functions are useful for representing situations with different rules or conditions that apply to different parts of the problem. They allow for more flexibility and accuracy in mathematical modeling and problem-solving.
Why Are Piecewise Functions Important in Circuit Training?
Circuit training is a popular form of exercise that involves performing a series of different exercises in a specific order, usually with little to no rest in between. It is a highly effective way to improve cardiovascular fitness, build strength, and burn calories. In order to create an effective circuit training routine, trainers often use piecewise functions to plan and organize the exercises.
Piecewise functions are mathematical functions that are defined by different formulas or rules depending on the value of the input. In circuit training, piecewise functions are used to determine the specific exercises, time intervals, and repetitions for each station or station block. This allows trainers to create a workout routine that targets different muscle groups, challenges different energy systems, and keeps the workout dynamic and engaging.
For example, a piecewise function may be used to determine the exercises and duration for a cardio-strength circuit. The function could be defined so that for the first 30 seconds, the participant performs high-intensity cardio exercises like jumping jacks or burpees. Then, for the next 30 seconds, the participant switches to strength exercises like push-ups or squats. This alternating pattern may continue for a predetermined number of intervals.
Using piecewise functions in circuit training allows trainers to easily modify and customize workouts for individuals with different fitness levels and goals. By adjusting the formulas or rules for each segment, trainers can create routines that are suitable for beginners, intermediate, and advanced participants. Additionally, piecewise functions help trainers ensure that each workout is well-rounded and targets all major muscle groups, promoting overall strength and balance in the body.
How to Solve Piecewise Functions in Circuit Training?
When it comes to solving piecewise functions in circuit training, there are a few key steps to follow. Piecewise functions involve multiple equations or expressions that define different parts of the function depending on the input value. Circuit training is a method that allows students to practice solving mathematical problems in a structured and engaging way.
To solve piecewise functions in circuit training, the first step is to determine which equation or expression applies to the given input value. This can be done by examining the breakpoints or domain boundaries provided in the function. Once the correct equation or expression is identified, the next step is to evaluate it using the given input value.
It is important to pay attention to any specifications or restrictions mentioned in the problem, as these can affect the validity of certain equations or expressions within the piecewise function. Additionally, students should be familiar with the properties and rules of the mathematical operations involved, such as addition, subtraction, multiplication, and division.
- Step 1: Identify the equation or expression corresponding to the given input value.
- Step 2: Evaluate the equation or expression using the input value.
- Step 3: Consider any specifications or restrictions mentioned in the problem.
- Step 4: Apply the appropriate mathematical operations to solve the equation or expression.
By following these steps and practicing with circuit training exercises, students can improve their skills in solving piecewise functions. Circuit training offers a dynamic and interactive approach to learning, allowing students to engage with the material in a hands-on manner. It also helps reinforce their understanding of the concepts and techniques involved in solving piecewise functions.
Common Challenges in Circuit Training with Piecewise Functions
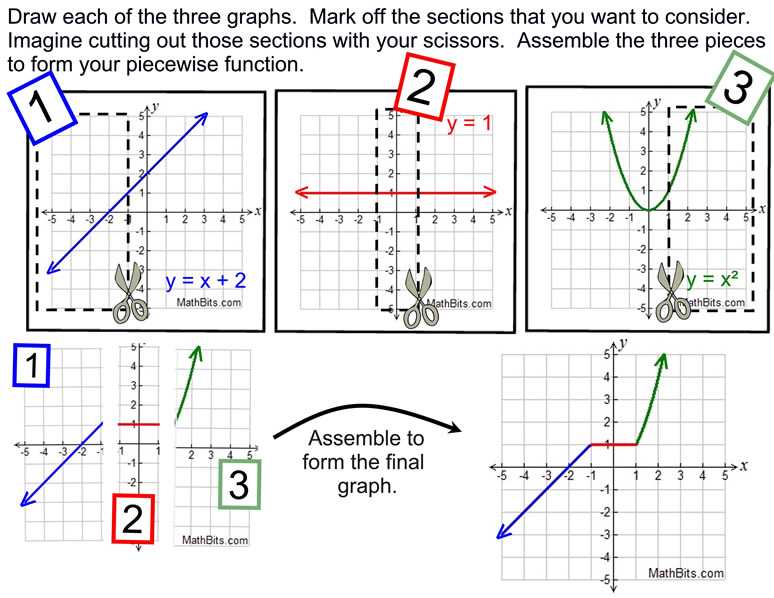
When it comes to circuit training with piecewise functions, there are several common challenges that students often face. One of the main challenges is understanding how to break down the function into its different pieces and identify the domains of each piece. This can be particularly difficult when dealing with complex piecewise functions that involve multiple conditions and intervals. Students must be able to correctly analyze each piece of the function and determine the appropriate domain for each.
Another challenge in circuit training with piecewise functions is graphing the function accurately. This requires students to have a strong understanding of how to plot points and connect them to create a graph of the function. They must also be able to accurately label the points and axes on the graph. Additionally, students need to be able to interpret the graph and understand how it represents the different pieces of the function.
Students may also struggle with solving equations involving piecewise functions. This can include finding the x-values that satisfy a particular condition or determining the output values for a given input. It requires careful analysis of the different cases and consideration of the domains of each piece of the function. Students must be able to effectively use algebraic techniques to solve the equations and obtain the correct solutions.
Overall, circuit training with piecewise functions presents unique challenges that require students to have a strong understanding of how to analyze, graph, and solve equations involving these types of functions. With practice and proper instruction, students can develop the necessary skills to overcome these challenges and successfully navigate circuit training exercises with piecewise functions.
Tips and Strategies for Solving Piecewise Functions in Circuit Training
When solving piecewise functions in circuit training exercises, it is important to understand the structure and behavior of the different pieces of the function. This can help simplify the task at hand and make the process more manageable. Here are some tips and strategies to help you tackle these types of problems effectively:
- Identify the different pieces: The first step in solving piecewise functions is to identify the different pieces or intervals of the function. Pay close attention to any given conditions or restrictions that define these intervals. For example, a function might have different rules or formulas depending on whether the input is positive or negative.
- Work systematically: When dealing with multiple pieces of a piecewise function, it can be helpful to work systematically. Start with the first interval or piece and solve for the given condition or restriction. Then, move on to the next interval and repeat the process. This can help prevent confusion and ensure that you're addressing each part of the function correctly.
- Keep track of your steps: It's important to keep track of the steps you take when solving piecewise functions. This can help you stay organized and avoid mistakes along the way. Consider writing down each step of your calculations or using a table to keep track of the values and equations for each piece of the function.
- Check for continuity: One of the key aspects of piecewise functions is continuity. Make sure to check if the different pieces of the function are continuous or if there are any discontinuities, such as jumps or holes. This can help you verify your solutions and ensure that the function behaves as expected.
- Practice, practice, practice: Like any other mathematical concept, solving piecewise functions requires practice. The more familiar you become with these types of problems, the easier they will become. Make it a habit to solve circuit training exercises regularly to build your skills and confidence.
By following these tips and strategies, you can approach and solve piecewise functions in circuit training exercises with greater ease and efficiency. Remember to stay organized, pay attention to the details, and practice regularly to improve your problem-solving abilities in this area.
Examples of Circuit Training Piecewise Functions Answers
In the previous sections, we discussed the concept of circuit training and piecewise functions. Now, let's take a look at some examples of circuit training piecewise functions and their corresponding answers.
Example 1:
Consider the following piecewise function:
f(x) = {
x + 3, if x < 0,
2x + 1, if 0 ≤ x < 3,
x^2, if x ≥ 3
}
To evaluate this function, we need to check which condition is satisfied based on the input value of x. Let's calculate the answers for some specific values of x:
- For x = -2, the condition x < 0 is satisfied. Therefore, f(-2) = (-2) + 3 = 1.
- For x = 1, the condition 0 ≤ x < 3 is satisfied. Therefore, f(1) = 2(1) + 1 = 3.
- For x = 4, the condition x ≥ 3 is satisfied. Therefore, f(4) = (4)^2 = 16.
Example 2:
Let's consider another piecewise function:
g(x) = {
-2x, if x ≤ -1,
x^2 - 1, if -1 < x < 2,
3x + 4, if x ≥ 2
}
Now, let's calculate the answers for some specific values of x:
- For x = -3, the condition x ≤ -1 is satisfied. Therefore, g(-3) = -2(-3) = 6.
- For x = 0, the condition -1 < x < 2 is satisfied. Therefore, g(0) = (0)^2 - 1 = -1.
- For x = 3, the condition x ≥ 2 is satisfied. Therefore, g(3) = 3(3) + 4 = 13.
These were just a couple of examples to illustrate how to evaluate circuit training piecewise functions. Remember that the key is to check which condition is satisfied based on the input value of x, and then calculate the corresponding answer.
By practicing more and working on different examples, you can become proficient in solving circuit training piecewise functions. Keep practicing and exploring new problems to enhance your understanding of this topic.