In the world of geometry, worksheets are an essential tool for students to practice and reinforce their understanding of various concepts. These worksheets often come with questions and problems that require students to apply their knowledge of geometric principles and solve them. Geometry 1.5 worksheet answers are a valuable resource for both teachers and students alike, as they provide a means to check the accuracy of their answers and identify any areas for improvement.
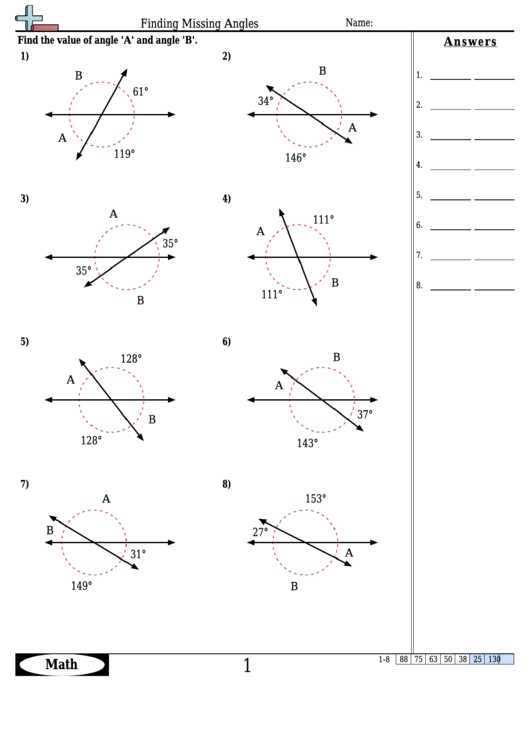
Geometry 1.5 worksheets typically cover topics such as angles, lines, and polygons. Students may be asked to identify different types of angles, such as acute, obtuse, or right angles, and determine their measures. They may also need to classify different types of lines, such as parallel, perpendicular, or intersecting lines, and understand how to use mathematical notation to represent them.
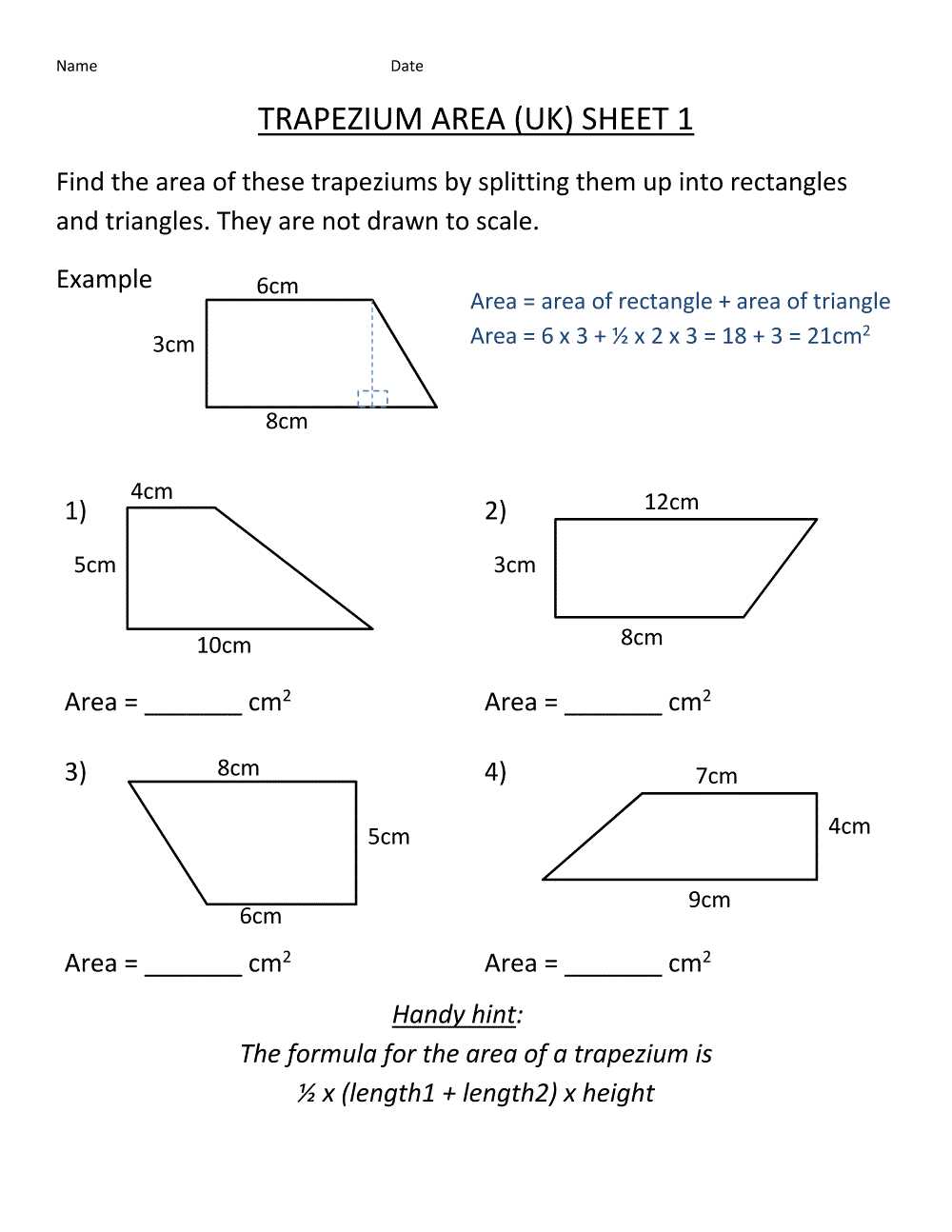
Another topic that may be covered in Geometry 1.5 worksheets is polygons. Students may be required to identify different types of polygons, such as triangles, quadrilaterals, or pentagons, based on their characteristics and properties. They may also need to calculate the perimeter or area of various polygons using appropriate formulas and measurements.
Geometry 1.5 worksheet answers provide a comprehensive solution to these types of problems, allowing students to check their work and ensure they have a solid understanding of the concepts being covered. With these answers, teachers can also assess their students’ progress and provide targeted feedback and guidance to help them improve their skills in geometry.
Geometry 1.5 Worksheet Answers: Mastering Geometric Principles

In geometry, understanding and applying geometric principles is essential to solving problems and proving theorems. Geometry 1.5 worksheet serves as practice material for students to solidify their understanding of these concepts. The answers to this worksheet provide a guide for students to assess their own performance and improve their geometry skills.
The worksheet covers various topics, including angle relationships, parallel lines, and triangle properties. By solving the problems on the worksheet and checking their answers, students can identify any areas of weakness and focus on improving their understanding of these geometric principles.
To master geometric principles, it is crucial to have a solid foundation of basic concepts. The worksheet answers help students verify their knowledge and identify any misconceptions they may have. They can use this feedback to seek additional help if needed and clarify any doubts or uncertainties they may have.
By practicing with the Geometry 1.5 worksheet and checking their answers, students can reinforce their understanding of geometric principles. This practice not only improves their problem-solving skills but also enhances their ability to apply geometric concepts in real-world situations. Additionally, it helps students develop logical reasoning and critical thinking skills, which are essential in the study of geometry and other mathematical disciplines.
In conclusion, the Geometry 1.5 worksheet answers play a vital role in mastering geometric principles. They serve as a tool for self-assessment, providing students with feedback to improve their understanding of geometric concepts. By practicing and checking their answers, students can solidify their knowledge and develop their problem-solving skills, leading to a more comprehensive understanding of geometry.
Understanding Geometric Concepts
Geometry is a branch of mathematics that deals with the study of shapes, sizes, and properties of figures. It is essential to understand various geometric concepts to solve problems and analyze real-world situations accurately. By having a solid foundation in geometry, one can develop problem-solving skills and logical reasoning abilities.
Points, lines, and planes: In geometry, a point is a location that has no size or shape. A line is a straight path with no thickness and extends infinitely in both directions. A plane is a flat surface that extends infinitely in all directions and has no thickness. These fundamental concepts form the basis of geometric relationships.
Angles and polygons: An angle is a measure of the amount of rotation between two rays that share a common endpoint. It is typically measured in degrees or radians. Polygons are closed figures with straight sides, and their properties depend on the number of sides they have. Understanding the properties of angles and polygons helps in determining the symmetry, congruence, and similarity of shapes.
Circles and spheres: A circle is a set of points equidistant from a fixed point called the center. It is defined by its radius, which is the distance from the center to any point on the circle. Circles have several unique properties, such as tangents, chords, and secants. Similarly, in three-dimensional geometry, a sphere is a set of points equidistant from a fixed point called the center. It plays a significant role in determining the volume and surface area of three-dimensional objects.
Transformations and coordinate geometry: Transformations involve changing the position, shape, or size of a figure. The core transformations include translation, reflection, rotation, and dilation. Coordinate geometry connects algebraic equations with geometric representations. It involves plotting points on a coordinate plane and determining the relationship between their coordinates.
Understanding geometric concepts is essential for various fields, including architecture, engineering, and design. It enables us to analyze and describe the physical world around us accurately. By applying the knowledge of geometry, we can solve problems and make informed decisions in a wide range of disciplines.
Exploring Geometric Properties
In the study of geometry, one of the main goals is to understand and describe the properties of different shapes and objects. These properties can help us analyze and solve problems involving them. By exploring the geometric properties of shapes, we can uncover relationships between their angles, sides, and areas, and gain a deeper understanding of the structure and organization of our physical world.
Angles: One important geometric property is angles. Angles are formed when two lines or line segments meet at a point. They can be classified as acute, obtuse, or right angles based on their measures. Acute angles are less than 90 degrees, obtuse angles are greater than 90 degrees, and right angles measure exactly 90 degrees.
Sides: Another crucial property to consider is the length of the sides of a shape. In geometry, sides refer to the line segments that connect the vertices of a shape. These sides can be equal in length, which is often the case in symmetrical shapes like squares and equilateral triangles, or they can have different lengths, which is typical in irregular shapes like rectangles and scalene triangles.
Areas: The area is a property that refers to the amount of space occupied by a shape in a two-dimensional plane. It is typically measured in square units. The formula for finding the area of common geometric shapes, such as squares, rectangles, and triangles, is well-known. By calculating the areas of different shapes, we can compare their sizes and determine the amount of space they cover.
- Perimeters: Perimeter refers to the total length of the boundaries of a shape. It is the sum of the lengths of all its sides. By calculating the perimeters of different shapes, we can determine how long their boundaries are and analyze their overall size and shape.
- Congruence: Congruence is a property that describes when two shapes have exactly the same size and shape. When two shapes are congruent, their corresponding angles and sides are equal. By exploring congruence, we can identify shapes that are identical to each other and use the properties of known shapes to solve problems involving unknown ones.
By exploring these and other geometric properties, we can deepen our understanding of the fundamental principles of geometry and apply them in various real-life situations. Whether we are designing buildings, planning road networks, or analyzing the patterns in nature, a solid understanding of geometric properties is crucial for solving problems and making informed decisions.
Applying Geometric Transformations

In geometric transformations, various techniques are used to manipulate and manipulate shapes and figures in different ways. These transformations include translations, rotations, reflections, dilations, and combinations of these operations. Each transformation has specific properties and effects on the original figure, providing a unique way to explore and analyze mathematical concepts related to shape and space.
Translations involve moving an object from one location to another without changing its size or shape. This transformation is often represented by giving the horizontal and vertical shifts in the form of ordered pairs. Translations can be performed in any direction, allowing for the exploration of symmetry, congruence, and the relationship between different parts of a figure.
Rotations involve turning an object around a fixed point, known as the center of rotation. The amount of rotation is measured in degrees, and positive angles indicate counterclockwise rotations, while negative angles indicate clockwise rotations. Rotations can create symmetry, define congruence, and highlight the relationship between the original figure and its image.
Reflections involve flipping an object over a line called the line of reflection. This transformation creates a mirror image of the original figure and preserves the distance between corresponding points. Reflections can be performed over horizontal lines, vertical lines, and diagonal lines, allowing for the exploration of symmetry, congruence, and transformations in two dimensions.
Dilations involve enlarging or reducing an object by a scale factor. This transformation preserves the shape of the original figure but changes its size. Dilations can be performed relative to a point, known as the center of dilation, and the scale factor determines the amount of enlargement or reduction. This transformation allows for the exploration of similarity, proportionality, and the relationship between different parts of a figure.
Solving Geometric Equations
Geometry involves the study of shapes and their properties. Solving geometric equations is an essential part of this branch of mathematics. It allows us to find the values of unknown variables that satisfy specific geometric relationships. By solving these equations, we can determine the measurements of angles, lengths of sides, and other properties of geometric figures.
One type of geometric equation commonly encountered is the equation involving angles. For example, given a triangle, we may be asked to find the measure of one of its angles. To do this, we can use the properties of triangles, such as the fact that the sum of the measures of the angles in any triangle is always 180 degrees. By setting up and solving equations based on these properties, we can find the desired angle.
Another type of geometric equation involves finding the lengths of sides or the areas of figures. These equations often require the application of formulas derived from geometry. For example, to find the area of a rectangle, we can use the formula A = length * width. By rearranging this equation, we can solve for either the length or the width if the area is known.
Overall, solving geometric equations requires a solid understanding of geometric principles and the ability to apply mathematical concepts and formulas. It is an important skill that allows us to solve real-world problems involving shapes and measurements. By mastering this skill, we can navigate the complexities of geometry and unlock the beauty and practicality of this field of mathematics.
Analyzing Geometric Proofs
Geometric proofs are an essential part of mathematics, specifically in the field of geometry. These proofs involve logical reasoning and deductions to demonstrate the validity of a geometric statement or theorem. Analyzing geometric proofs requires a deep understanding of the properties and relationships of geometric figures.
One important aspect of analyzing geometric proofs is identifying the given information and objectives. These proofs usually begin with a set of givens, which are the statements or facts that are known to be true. The objectives, on the other hand, are the statements that need to be proven or derived based on the given information.
A crucial step in analyzing geometric proofs is applying deductive reasoning. Deductive reasoning involves using logic and known facts to draw logical conclusions. It is essential to carefully follow the logical structure of the proof, identifying the steps and justifications. Each step should be logically connected to the previous ones, leading to the final objective.
Furthermore, analyzing geometric proofs also entails using geometric properties and theorems. These properties include things like congruence, similarity, parallel lines, perpendicular lines, and angles. The theorems provide established rules and relationships between geometric figures. It is necessary to have a solid understanding of these properties and theorems to effectively analyze and solve geometric proofs.
Reviewing Geometry 1.5 Worksheet Tasks

In this article, we have reviewed the tasks found in the Geometry 1.5 worksheet. These tasks were designed to test students’ understanding of various geometric concepts and their ability to apply these concepts to solve problems. Overall, the tasks covered a range of topics including angles, lines, and shapes.
Some of the key concepts that were assessed in the worksheet include:
- Angle types: Students had to identify and classify different types of angles, such as acute, obtuse, and right angles.
- Angle measurements: Students were required to measure angles using a protractor and calculate the missing angle measurements in a given figure.
- Lines and line segments: Students had to identify and distinguish between various types of lines and line segments, such as parallel, perpendicular, and intersecting lines.
- Properties of shapes: Students needed to apply their knowledge of shape properties to solve problems and determine missing measurements of sides and angles in different shapes.
The tasks in the Geometry 1.5 worksheet provided a comprehensive assessment of students’ understanding and proficiency in these geometric concepts. By successfully completing these tasks, students demonstrated their ability to apply their knowledge to real-world situations and solve problems related to geometry.
Overall, the Geometry 1.5 worksheet offered a valuable opportunity for students to reinforce their understanding of key geometric concepts and develop their problem-solving skills. By reviewing the tasks in this worksheet, students can identify areas of improvement and further enhance their knowledge and skills in geometry.