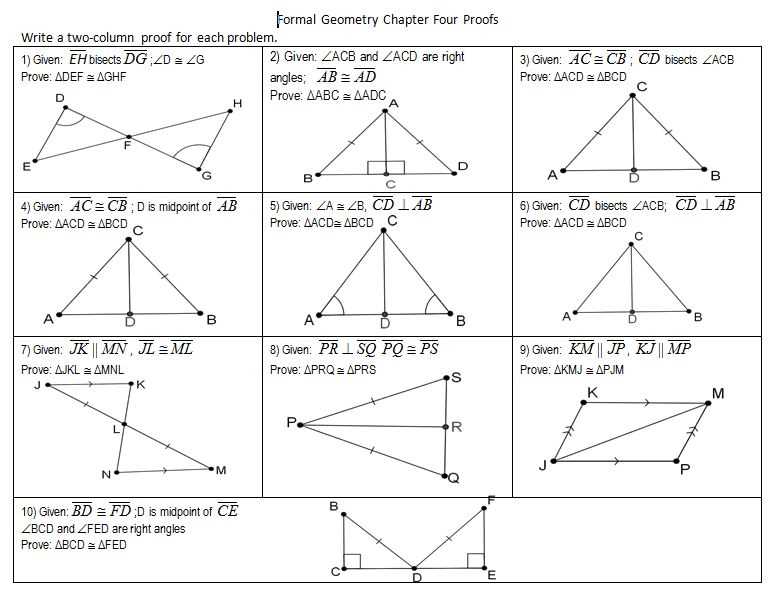
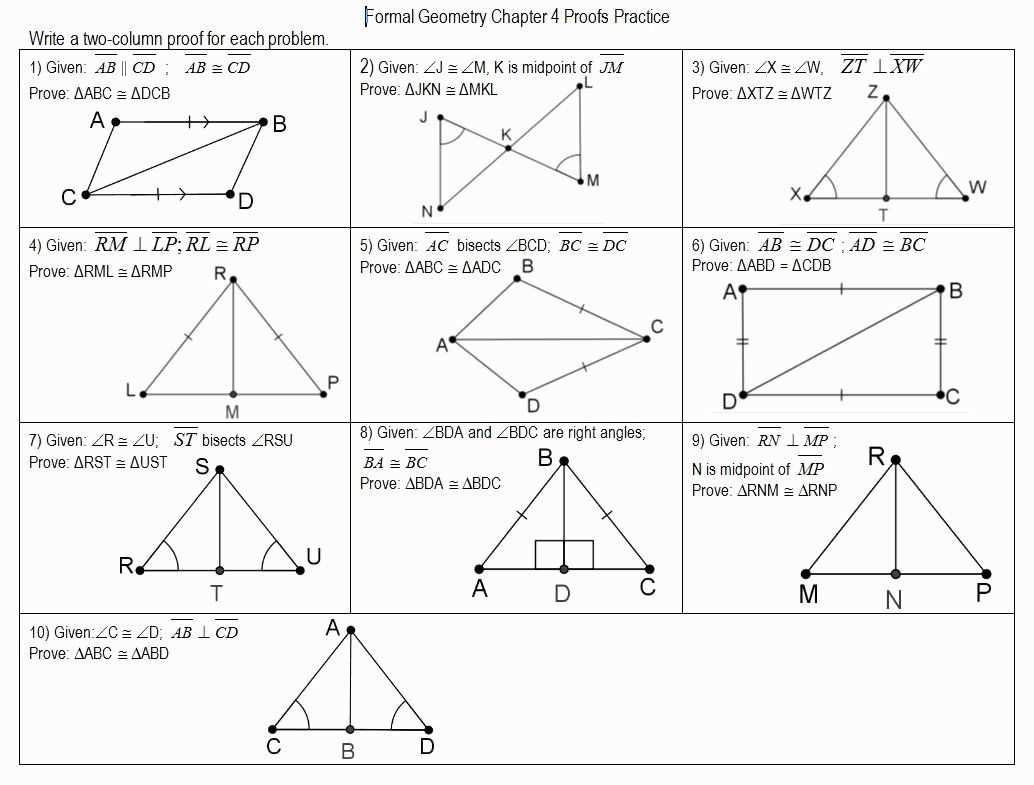
Welcome to our guide to the answers for the Geometry 6.1 worksheet. In this article, we will provide you with step-by-step solutions to the questions posed in the worksheet. Geometry 6.1 focuses on angles and their measurements, giving students a deeper understanding of the different types of angles and how to calculate their measures.
In the first section of the worksheet, students are asked to identify the different types of angles, such as acute, obtuse, right angles, and straight angles. Our answer guide will provide clear explanations and visual representations to help students differentiate between these angles.
The second section of the worksheet delves into angle measurements, asking students to calculate the measures of various angles using the given information. We will break down each problem step by step, providing the necessary formulas and calculations to find the correct answers.
By following our comprehensive guide, students will gain a solid understanding of angles and their measurements, enabling them to confidently solve similar problems on their own. Whether you are a student, teacher, or parent looking for extra resources, our Geometry 6.1 worksheet answers will be a valuable tool to enhance your understanding of this topic.
Geometry 6.1 Worksheet Answers: Mastering the Basics
Geometry is a fundamental branch of mathematics that deals with the properties and relationships of points, lines, shapes, and figures. In order to develop a strong foundation in geometry, it is important to master the basics. One way to do this is by completing worksheet exercises that test your understanding of key concepts.
The Geometry 6.1 worksheet focuses on various topics, including angles, lines, and polygons. It is designed to assess your understanding of the properties and characteristics of these geometric elements. By answering the questions in this worksheet, you can evaluate your knowledge and identify any areas that require further study and improvement.
Angles:
One of the main topics covered in the Geometry 6.1 worksheet is angles. You will be asked to identify different types of angles, such as acute, obtuse, right, and straight angles. Additionally, you will need to apply your understanding of angle measurements and relationships, including complementary and supplementary angles.
Lines:
Another important focus of the Geometry 6.1 worksheet is lines. You will encounter questions that test your knowledge of various types of lines, such as parallel, perpendicular, and intersecting lines. It is crucial to remember the properties and characteristics of these lines in order to correctly answer the questions asked.
Polygons:
The Geometry 6.1 worksheet also includes questions on polygons. You will need to identify different types of polygons, such as triangles, quadrilaterals, and pentagons. Furthermore, you will be required to calculate various measures of these polygons, including their perimeter and area.
By completing the Geometry 6.1 worksheet and checking your answers, you will be able to gauge your understanding of the basics of geometry. If you find that you have made any errors or have difficulty with certain topics, it is recommended to review the relevant concepts and seek additional practice. With continued practice and mastery of the basics, you will be well-prepared to tackle more advanced geometry exercises and concepts.
Understanding the Concept of Parallel Lines and Transversals
The concept of parallel lines and transversals is an important aspect of geometry. Parallel lines are lines that never intersect, meaning they are always the same distance apart. Transversals, on the other hand, are lines that intersect two or more parallel lines at different points. By studying the relationship between parallel lines and transversals, we can gain a deeper understanding of various geometric properties and theorems.
One key concept related to parallel lines and transversals is the corresponding angles theorem. According to this theorem, when a transversal intersects two parallel lines, the corresponding angles formed are congruent. In other words, if we have two parallel lines intersected by a transversal, the angles in the same position on each line will be equal. This theorem allows us to determine the measures of angles in a geometric figure by identifying corresponding angles.
Another important concept is the alternate interior angles theorem. When a transversal intersects two parallel lines, the alternate interior angles formed are congruent. Alternate interior angles are those that are on opposite sides of the transversal and inside the two parallel lines. This theorem helps us prove the congruence of angles in different situations and solve various geometric problems.
Parallel lines and transversals also play a role in the understanding of angle relationships, such as vertical angles, linear pairs, and supplementary angles. By studying the angles formed by parallel lines and transversals, we can determine these angle relationships and use them to solve equations and problems involving angles.
In conclusion, understanding the concept of parallel lines and transversals is fundamental in geometry. It allows us to apply theorems like the corresponding angles theorem and the alternate interior angles theorem to solve geometric problems. By studying the relationships between angles formed by parallel lines and transversals, we can deepen our understanding of various angle relationships and the properties of geometric figures.
Solving Problems Involving Corresponding Angles and Alternate Interior Angles
When working with angles in geometry, there are certain relationships that can help us solve various problems. Two of these relationships are corresponding angles and alternate interior angles. Understanding these relationships can make problem-solving tasks much easier.
Corresponding angles are formed when a transversal line intersects two parallel lines. Corresponding angles are located in the same position in relation to the transversal line and the parallel lines. This means that they have equal measures. For example, if one corresponding angle measures 50 degrees, then the other corresponding angle in the same position will also measure 50 degrees.
Alternate interior angles are also formed when a transversal line intersects two parallel lines. These angles are located on opposite sides of the transversal line, between the parallel lines. Alternate interior angles are congruent, which means they have equal measures. If one alternate interior angle measures 70 degrees, then the other alternate interior angle will also measure 70 degrees.
By recognizing these relationships and using them to solve problems, we can find missing angle measures, prove the congruence of angles, or determine the relationships between angles. For example, if we know the measures of two corresponding angles, we can find the measure of another angle by subtracting or adding. Similarly, if we know the measure of one alternate interior angle, we can find the measure of another angle by subtracting or adding.
In conclusion, understanding the relationships between corresponding angles and alternate interior angles can greatly assist in solving geometry problems. These relationships allow us to determine unknown angle measures, prove congruence, and find other angle relationships. By applying these concepts, we can approach geometry problems with greater confidence and accuracy.
Applying the Angle Relationships Theorems: Same-Side Interior Angles and Alternate Exterior Angles

The Angle Relationships Theorems, specifically the Same-Side Interior Angles and Alternate Exterior Angles, are important concepts in geometry that help us understand the relationships between angles formed by parallel lines and a transversal. These theorems provide us with useful insights into the properties of angles and their measurements.
Same-Side Interior Angles theorem states that when two parallel lines are intersected by a transversal, the interior angles on the same side of the transversal are supplementary. In other words, the sum of the same-side interior angles is always equal to 180 degrees. This theorem is helpful in determining the measurements of angles in various geometric figures.
The Alternate Exterior Angles theorem states that when two parallel lines are cut by a transversal, the exterior angles on the opposite sides of the transversal are congruent. In simpler terms, the alternate exterior angles are equal in measure. This theorem allows us to establish relationships between angles that are formed by parallel lines and a transversal, helping us solve problems involving angle measurements.
By applying these Angle Relationships Theorems, we can confidently identify the properties of angles formed by parallel lines and a transversal and make accurate calculations. Understanding these theorems and their applications is crucial in geometry, as they provide a foundation for solving more complex problems and analyzing geometric figures.
Exploring the Properties of Supplementary and Vertical Angles
When studying geometry, one of the fundamental concepts we come across is that of angles. Angles are formed when two rays have a common endpoint, known as the vertex. In this exploration, we will focus on two specific types of angles: supplementary and vertical angles.
Supplementary angles are those whose measures add up to 180 degrees. This means that when two angles are supplementary, they form a straight line. For example, if angle A measures 70 degrees, then angle B, which is supplementary to angle A, would measure 110 degrees. Supplementary angles are often found in problems involving parallel lines and transversals, where corresponding angles are congruent.
Vertical angles are formed when two lines intersect. They are opposite each other and have equal measures. Vertical angles are also known as opposite angles or vertically opposite angles. For example, if line AB intersects line CD, angle 1 and angle 3 are vertical angles, and angle 2 and angle 4 are vertical angles. Vertical angles are useful in proving theorems and solving problems involving angles.
To summarize, supplementary angles are angles that add up to 180 degrees, while vertical angles are formed when two lines intersect and are opposite each other. Understanding the properties of these angles is crucial in geometry, as it helps us analyze and solve various geometric problems and proofs.
Identifying and Using the Angle Sum and Exterior Angle Theorems
The Angle Sum and Exterior Angle Theorems are fundamental concepts in geometry that help us understand the relationships between angles in polygons. These theorems provide us with valuable information that can be used to solve various geometric problems and prove mathematical statements.
The Angle Sum Theorem states that the sum of the interior angles of a polygon, with n sides, is equal to (n-2) times 180 degrees. This means that if we know the number of sides of a polygon, we can easily calculate the sum of its interior angles. For example, a triangle, which has three sides, will have a total interior angle sum of (3-2) x 180 = 180 degrees.
The Exterior Angle Theorem, on the other hand, states that the measure of each exterior angle of a polygon is equal to the sum of its two non-adjacent interior angles. This theorem allows us to find the measurement of an exterior angle when we know the measurements of the interior angles of a polygon. For instance, if we have a quadrilateral with interior angle measurements of 60 degrees, 90 degrees, and 120 degrees, we can find the measurement of each exterior angle by adding the two non-adjacent interior angles: 60 + 120 = 180 degrees.
By understanding and applying these theorems, we can solve problems involving polygons, such as finding missing angle measurements or proving that certain angles are congruent. These theorems are powerful tools that allow us to analyze the properties of polygons and gain a deeper understanding of their characteristics.
In conclusion, the Angle Sum and Exterior Angle Theorems provide crucial information about the angles in polygons. By utilizing these theorems, we can solve problems and prove mathematical statements related to angles in polygons. These theorems are essential tools in the study of geometry and enable us to explore the intricate relationships between different angles in polygons.
Testing Your Knowledge with Practice Problems and Interactive Worksheets
Now that you have learned about geometry concepts in the 6.1 worksheet, it’s time to test your knowledge with practice problems and interactive worksheets. These resources will help you reinforce and apply what you have learned in a hands-on manner.
Practice Problems:
You can start by solving practice problems that cover the concepts from the 6.1 worksheet. These problems will allow you to practice identifying geometric shapes, calculating angles, and solving related problems. You can find practice problems in your textbook, online resources, or worksheets provided by your teacher.
Interactive Worksheets:
To further enhance your understanding and engagement, you can also try interactive worksheets. These worksheets are designed to provide a more interactive and dynamic learning experience. They often include activities such as dragging and dropping shapes, measuring angles with virtual tools, and solving problems through interactive simulations. Online educational platforms and geometry websites offer various interactive worksheets that cater to different geometry topics.
Benefits of Practice and Interactive Worksheets:
- Reinforcement: Practice problems and interactive worksheets help reinforce the concepts and principles you have learned in the 6.1 worksheet. By solving problems and engaging in interactive activities, you can solidify your understanding of geometry concepts.
- Application: These resources allow you to apply your knowledge in real-life scenarios. They often present problems and situations that require you to use geometry concepts to find solutions. This application helps you develop practical problem-solving skills.
- Engagement: Interactive worksheets make learning geometry more engaging and fun. The interactive nature of the activities keeps you actively involved, which can enhance your interest and motivation to learn.
- Identifying areas of improvement: By practicing with problems and worksheets, you can identify areas where you need more practice or further clarification. This feedback can guide you in seeking additional help or revisiting specific concepts.
Remember, the key to mastering geometry is consistent practice and active engagement with the subject. Using practice problems and interactive worksheets will help you build a strong foundation and boost your confidence in geometry.
So, go ahead and start solving practice problems and exploring interactive worksheets to solidify your knowledge of geometry concepts covered in the 6.1 worksheet!
Q&A:
What are practice problems and interactive worksheets?
Practice problems and interactive worksheets are educational resources that allow you to test your knowledge and understanding of a particular subject or topic. These resources typically contain a series of questions or exercises that you can solve or complete to practice and reinforce your understanding of the subject.
Why are practice problems and interactive worksheets useful?
Practice problems and interactive worksheets are useful because they provide a hands-on approach to learning. By actively engaging with the content and solving problems, you can better understand and retain information. These resources also allow you to identify any areas where you may need additional practice or review.
How can I find practice problems and interactive worksheets?
You can find practice problems and interactive worksheets in a variety of places. Many educational websites and online learning platforms offer these resources for free or for a fee. You can also find them in textbooks, study guides, or through a simple internet search.
What subjects or topics can I find practice problems and interactive worksheets for?
You can find practice problems and interactive worksheets for a wide range of subjects and topics. Common subjects include math, science, language arts, and social studies. However, you can also find practice problems and interactive worksheets for more specialized topics such as computer programming, music theory, or foreign languages.