
Welcome to our guide on Geometry 6.4 Worksheet Answers. In this article, we will provide you with the solutions to the questions on a geometry worksheet. Specifically, we will focus on mastering geometric proofs, as this is an important concept in geometry. By understanding how to write and analyze geometric proofs, you will develop a strong foundation in the subject and be better prepared for more advanced topics in mathematics.
Geometry 6.4 focuses on proving triangles congruent using the SSS (Side-Side-Side) and SAS (Side-Angle-Side) congruence postulates. These postulates allow us to determine whether two triangles are congruent based on the information given about the sides and angles of the triangles. In order to prove congruence, we must show that the corresponding sides and angles of the triangles are congruent.
This worksheet provides various scenarios for proving congruence using the SSS and SAS postulates. It requires students to apply their knowledge of triangle congruence criteria and logical reasoning skills to construct valid proofs. By practicing these types of problems, students will enhance their proof-writing skills and gain a deeper understanding of the concepts involved.
In this article, we will walk you through the answers to the questions on this Geometry 6.4 worksheet. We will provide step-by-step explanations of the geometric proofs and highlight key concepts and strategies. Whether you’re a student looking for assistance or a teacher seeking additional resources for your classroom, this guide will be a valuable tool for mastering geometric proofs.
Geometry 6.4 Worksheet Answers
If you are looking for the answers to the Geometry 6.4 worksheet, you have come to the right place. In this worksheet, you will be working with triangles and their properties. It is important to understand the concepts and formulas related to triangles in order to solve the problems correctly.
To start, let’s review some basic triangle properties:
- A triangle has three sides and three angles.
- The sum of the angles in a triangle is always 180 degrees.
- Triangles can be classified based on their sides and angles:
- An equilateral triangle has three equal sides and three equal angles of 60 degrees each.
- An isosceles triangle has two equal sides and two equal angles.
- A scalene triangle has no equal sides or angles.
- A right triangle has one angle measuring 90 degrees.
- An acute triangle has all angles measuring less than 90 degrees.
- An obtuse triangle has one angle measuring more than 90 degrees.
Now, let’s move on to the specific problems in the worksheet. Remember to use the given information and apply the appropriate formulas and theorems to find the unknown values. You may need to use the Pythagorean theorem, trigonometric ratios, or the properties of similar triangles.
It is important to show your work and clearly label your answers. This will help you and your teacher to understand your thought process and ensure that you are finding the correct solutions. If you are unsure about any step or have any questions, don’t hesitate to ask for clarification.
Once you have completed the worksheet, you can compare your answers to the answer key provided. This will allow you to check your understanding and identify any mistakes or areas that need further review. Remember, practice makes perfect, so keep practicing and seeking help if needed.
Understanding the Concept of Geometry 6.4
In the study of geometry, it is important to have a solid understanding of the different concepts and principles that govern the field. One such concept that is covered in Geometry 6.4 is that of the angle-angle similarity theorem. This theorem states that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
This concept is fundamental to understanding the properties of similar triangles and can be used to solve a variety of problems in geometry. By recognizing and applying the angle-angle similarity theorem, students can determine whether two given triangles are similar and use that information to find missing side lengths or angles.
Example:
Given that angle A of triangle ABC is congruent to angle P of triangle PQR, and angle B of triangle ABC is congruent to angle Q of triangle PQR, we can conclude that triangles ABC and PQR are similar.
Once the similarity of the triangles is established, students can then utilize other properties of similar triangles, such as the proportionality of corresponding sides, to find missing measurements. This involves setting up and solving proportions based on the given information to find the values of the unknown variables.
Example:
Given that triangle ABC is similar to triangle DEF, and the length of side AB is 5 units, we can set up the proportion AB/DE = BC/EF to find the length of side EF.
Overall, understanding the concept of Geometry 6.4 and the angle-angle similarity theorem is essential for mastering the study of geometry. It allows students to analyze and solve problems involving similar triangles, providing them with a valuable tool for geometric reasoning and problem-solving.
Importance of Geometry 6.4 in Mathematics

Geometry 6.4 is an important topic in mathematics that focuses on angles and their relationships. Understanding this concept is crucial for students as it provides a foundation for more advanced geometric concepts and problem-solving skills.
One key aspect of Geometry 6.4 is the study of angle relationships within a triangle. Students learn about different types of angles, such as acute, obtuse, and right angles, and how they relate to the sides and vertices of a triangle. This knowledge is essential for solving various problems involving angles within triangles, such as finding missing angles or determining congruence between triangles.
Geometry 6.4 also teaches students about the properties of special triangles, such as isosceles and equilateral triangles. These triangles have unique characteristics that allow for easier calculations and problem-solving. By understanding the properties of these special triangles, students can quickly determine angles, side lengths, and relationships between the sides and angles of the triangle.
Furthermore, the concepts covered in Geometry 6.4 provide a solid foundation for more advanced geometry topics, including trigonometry and calculus. Trigonometric functions, such as sine, cosine, and tangent, rely heavily on the understanding of angles and their relationships within triangles. Without a solid understanding of Geometry 6.4, students may struggle with these more complex concepts.
In conclusion, Geometry 6.4 plays a crucial role in mathematics education. It provides students with the necessary tools to solve geometric problems, understand angle relationships, and build a strong foundation for more advanced mathematical concepts. By mastering Geometry 6.4, students can enhance their problem-solving skills and excel in higher-level mathematics.
Key Concepts and Formulas in Geometry 6.4
In Geometry 6.4, we focus on the properties and relationships of parallelograms. A parallelogram is a quadrilateral with two pairs of parallel sides. Understanding the key concepts and formulas related to parallelograms is crucial for solving problems involving these shapes.
Opposite sides: In a parallelogram, the opposite sides are parallel and congruent. This property allows us to solve for the measures of unknown sides or angles by using the given information.
Opposite angles: The opposite angles in a parallelogram are congruent. This means that if we know the measure of one angle, we can determine the measures of the other three angles.
Diagonals: A parallelogram has two diagonals, which are segments that connect opposite vertices. The diagonals of a parallelogram bisect each other, meaning they divide each other into two congruent segments.
Area: The area of a parallelogram can be found by multiplying the base (the length of one of the sides) by the height (the perpendicular distance between the base and the opposite side). The formula for finding the area of a parallelogram is A = base × height.
Perimeter: The perimeter of a parallelogram is the sum of all its sides. Since opposite sides in a parallelogram are congruent, we can calculate the perimeter by adding the lengths of two adjacent sides and multiplying by 2.
By understanding these key concepts and formulas, we can effectively solve problems involving parallelograms and make accurate calculations for their sides, angles, area, and perimeter. These concepts are fundamental not only in Geometry 6.4 but also in other areas of mathematics and real-world applications.
Step-by-Step Solution for Geometry 6.4 Worksheet
In this worksheet, we will be solving various problems related to geometry, specifically focusing on the concepts of angles and triangles. We will go through each problem step-by-step, providing explanations and calculations to help you understand the solutions thoroughly.
Problem 1: Find the value of angle A in the given figure.
To find the value of angle A, we need to use the properties of alternate interior angles. Since the figure has parallel lines, angles ACE and ADB are alternate interior angles. We know that the sum of the measures of alternate interior angles is equal to 180 degrees. Therefore, angle A is equal to 180 degrees minus the measure of angle ACE. To find the measure of angle ACE, we can use the fact that it is a right angle. Therefore, angle ACE is 90 degrees. Substituting this value into the equation, we get angle A = 180 – 90 = 90 degrees.
Problem 2: Determine whether the given triangles are similar.
To determine if the triangles are similar, we need to compare their corresponding sides and angles. If the corresponding angles are congruent and the corresponding sides are proportional, then the triangles are similar by the Angle-Angle Similarity postulate. In triangle ABC and triangle DEF, we can observe that angle A and angle D are congruent, angle C and angle E are congruent, and angle B and angle F are congruent. Additionally, the ratios of the corresponding sides are equal: AC/DF = BC/EF = AB/DE. Therefore, we can conclude that triangle ABC and triangle DEF are similar.
Problem 3: Find the length of segment AB in the given figure.
To find the length of segment AB, we need to use the Pythagorean Theorem. The figure forms a right triangle with sides of lengths 8 and 15. Using the theorem, which states that the square of the hypotenuse (AB) is equal to the sum of the squares of the other two sides, we can set up the equation: AB^2 = 8^2 + 15^2. Simplifying the equation, we get AB^2 = 64 + 225 = 289. Taking the square root of both sides, we find that the length of segment AB is √289 = 17 units.
In this way, we will continue solving each problem in the worksheet, providing detailed explanations and step-by-step solutions. By following along and understanding these solutions, you will improve your understanding of geometry concepts and develop problem-solving skills in this subject.
Common Mistakes to Avoid in Geometry 6.4
Geometry 6.4 deals with the properties and relationships of parallelograms. It is important to understand the concepts and formulas involved in order to solve problems correctly. However, there are some common mistakes that students often make. By being aware of these mistakes, you can avoid them and improve your understanding of Geometry 6.4.
Mistake 1: Assuming All Quadrilaterals are Parallelograms
One common mistake is assuming that any four-sided figure is a parallelogram. In Geometry 6.4, a quadrilateral must meet specific criteria to be classified as a parallelogram. These criteria include having opposite sides that are parallel and congruent. It is important to carefully examine the given information and apply the appropriate properties and theorems to determine if a quadrilateral is a parallelogram.
Mistake 2: Incorrectly Applying the Properties of Parallelograms
Another common mistake is incorrectly applying the properties of parallelograms. For example, students may mistakenly assume that all angles in a parallelogram are right angles, which is not always the case. It is important to correctly identify and apply the properties of parallelograms, such as opposite angles being congruent and consecutive angles being supplementary. This can be done by carefully reading and interpreting the given information in the problem.
Mistake 3: Misusing the Formulas for Area and Perimeter
Geometry 6.4 also involves calculating the area and perimeter of parallelograms. One common mistake is misusing the formulas for these calculations. It is important to remember that the height of a parallelogram is the perpendicular distance between two parallel sides, and the base is a side of the parallelogram. Using the correct formulas and substituting the appropriate lengths will help you calculate the area and perimeter accurately.
Mistake 4: Not Using Consecutive Angles Correctly
Lastly, students may make a mistake when using consecutive angles in the properties and theorems of parallelograms. Consecutive angles are angles that share a side but are not adjacent. It is important to correctly identify and use consecutive angles in order to apply the properties and theorems correctly. This can be done by carefully examining the given information and identifying the angles that fit this criteria.
By avoiding these common mistakes, you will have a better understanding of Geometry 6.4 and be able to solve problems accurately and confidently.
Further Practice and Resources for Geometry 6.4
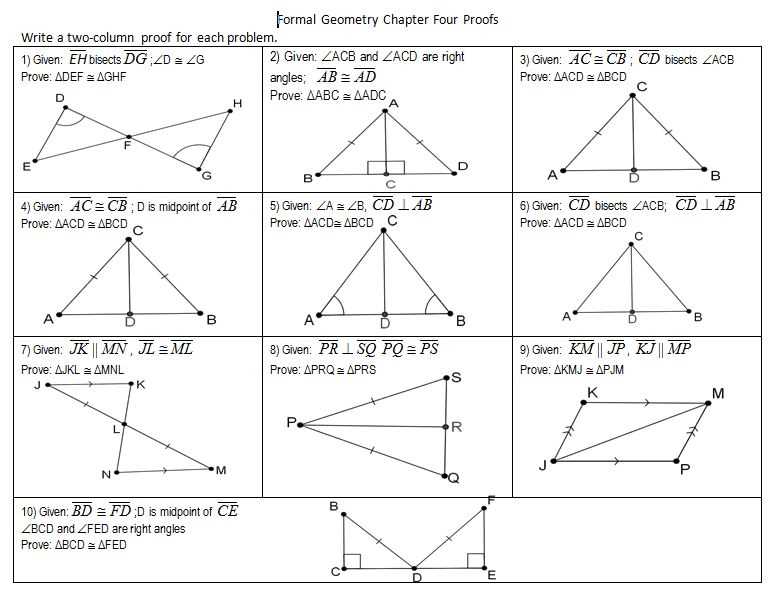
For additional practice with the concepts covered in Geometry 6.4, students can find various resources online. These resources include worksheets, interactive activities, and video tutorials, which can help reinforce their understanding of the topic.
Below is a list of recommended websites and online platforms that offer further practice and resources for Geometry 6.4:
- Mathway: This website provides step-by-step solutions to geometry problems, including those related to coordinate proof. Students can enter their specific problem and receive a detailed solution to help them better understand the concept.
- Khan Academy: Khan Academy offers a variety of geometry video lessons and practice exercises. Students can search for topics related to coordinate proofs and work through the interactive exercises to strengthen their skills.
- IXL Math: IXL Math is an online learning platform that offers a wide range of interactive math activities. Students can access geometry practice questions on coordinate proof and track their progress as they work through the exercises.
- MathisFun: MathisFun is a website that provides explanations and examples of various mathematical concepts. Students can find a section dedicated to coordinate proofs, which includes clear explanations and practice problems.
- Mathplanet: Mathplanet offers free online math courses, including geometry. Students can navigate to the geometry section and find lessons, practice exercises, and quizzes related to coordinate proof.
Remember that practice is essential for mastering any mathematical concept. By regularly using these resources and engaging in further practice, students can solidify their understanding of coordinate proof and improve their problem-solving skills.