
In this section, we dive into key concepts that are crucial for mastering the material presented in Chapter 6. The focus is on understanding the underlying principles and applying them effectively to various problems. With practice and a clear grasp of these ideas, success becomes inevitable.
By reviewing the steps involved in solving problems and familiarizing yourself with the most common types of questions, you can enhance your performance. Breaking down each problem systematically will help you build confidence and avoid mistakes. Understanding where and how to apply each principle is essential for solidifying your knowledge.
Additionally, addressing common pitfalls and providing helpful tips will aid in refining your skills. Through careful analysis and targeted practice, mastering this chapter is entirely achievable.
Comprehensive Review of Chapter 6
This section offers a thorough exploration of the fundamental topics introduced in Chapter 6, aimed at strengthening your understanding. The material emphasizes critical techniques and strategies that will be essential for solving various types of problems. A solid grasp of these principles is key to navigating more complex challenges.
Through a structured approach, we break down each concept into manageable parts, helping you to focus on core elements. This review is designed to reinforce your problem-solving skills, ensuring that you can tackle different types of exercises with confidence.
By revisiting important concepts and applying them to practice problems, you can ensure a deeper understanding and greater proficiency. With this approach, you will be well-prepared for any challenge that comes your way in this chapter.
Key Concepts Covered in Chapter 6
Chapter 6 introduces several essential ideas that are critical to solving related problems. These concepts provide the foundation for more advanced topics and serve as the building blocks for understanding the material in greater depth. Mastering these principles ensures a clear path to solving various challenges with confidence.
Among the key concepts, relationships between shapes and their properties play a significant role. The chapter delves into how different figures relate to one another and how these relationships can be applied to find solutions efficiently. Understanding these connections is crucial for simplifying complex problems.
Furthermore, the application of formulas and strategies to solve real-world scenarios is emphasized. This section highlights how to translate abstract concepts into tangible problem-solving methods, ensuring that students are well-equipped to tackle any challenges presented in this section.
How to Approach Chapter 6 Test Problems
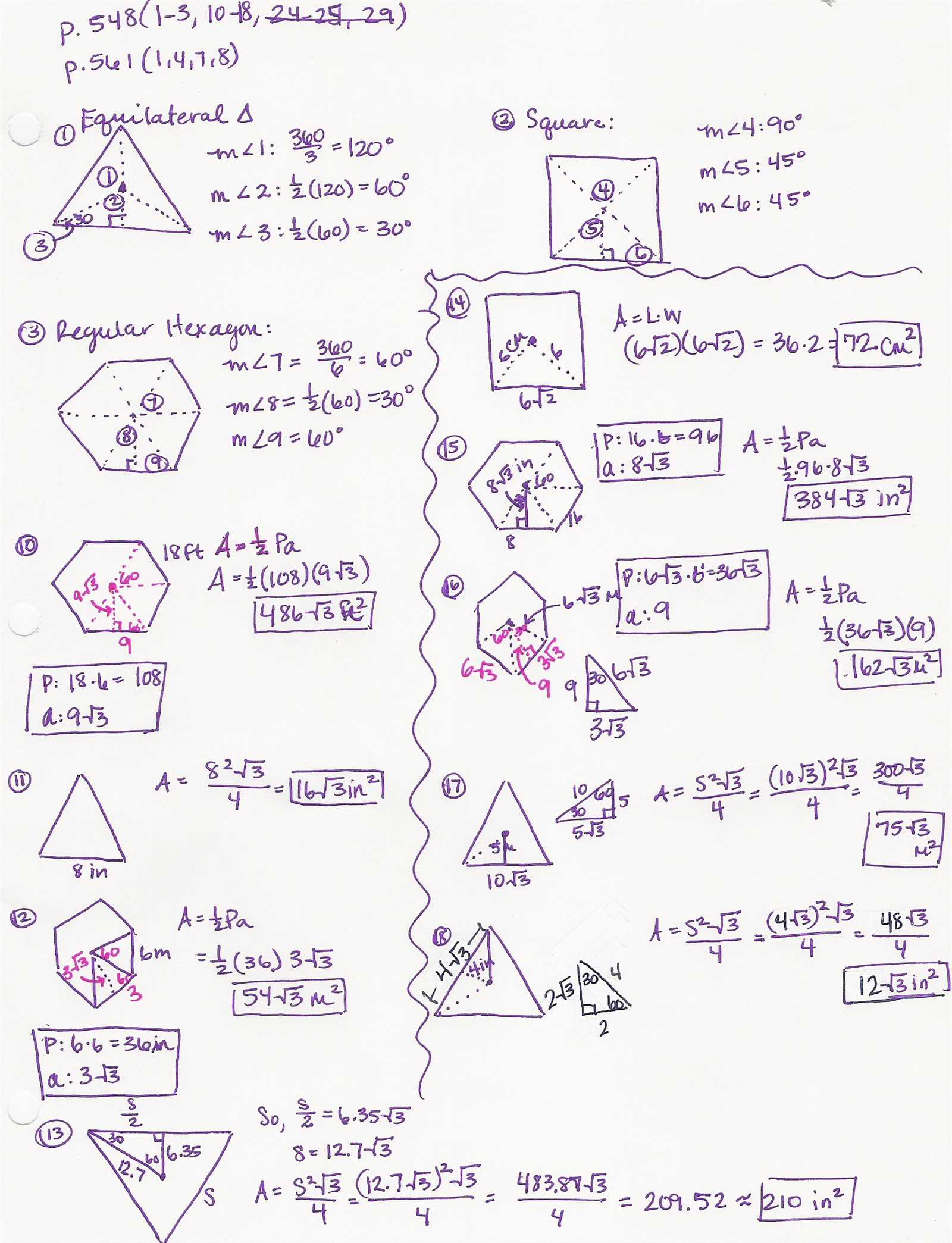
When facing problems from this chapter, it’s important to have a strategic approach. The key is to break down each question and identify which concepts are being tested. Taking time to understand the structure of each problem allows you to apply the most suitable method for solving it.
Understand the Problem’s Requirements
Before jumping into calculations, read the question carefully. Pay attention to the specific details and what is being asked. Identifying the key elements, such as figures or numerical values, will guide you in determining the proper steps to take.
Apply the Right Strategies
Once you’ve identified the necessary information, it’s time to apply the techniques learned in the chapter. Whether it involves using a formula or visualizing the problem with diagrams, using the right strategy is crucial for arriving at the correct solution. Don’t hesitate to review previous examples to see how similar problems were approached.
Step-by-Step Solutions for Practice Questions
In this section, we break down common problems into simple, manageable steps to help reinforce your understanding. By following the detailed solutions, you can see how each concept is applied in practice. These step-by-step explanations make complex problems more approachable and provide a clear roadmap to solve them effectively.
Example 1: Problem Solving with Equations
Let’s work through an example that requires using equations to find the unknown. Each step will guide you through the process of applying the correct principles to reach the solution.
| Step | Explanation | Result |
|---|---|---|
| 1 | Identify the variables and constants in the problem. | Variable = x, Constant = 5 |
| 2 | Set up the equation based on the given information. | x + 5 = 10 |
| 3 | Solve the equation for the unknown. | x = 5 |
Example 2: Visualizing and Solving with Diagrams
This example demonstrates how using diagrams can help simplify understanding. By visually representing the situation, you can apply the correct methods to find the solution.
| Step | Explanation | Result |
|---|---|---|
| 1 | Draw the shape based on the problem’s description. | Drawn triangle with labeled sides. |
| 2 | Use the properties of the shape to form an equation. | Use Pythagoras’ theorem. |
| 3 | Solve the equation to find the missing side length. | Side length = 8 |
Common Mistakes and How to Avoid Them
While solving problems, it’s easy to make certain errors that can lead to incorrect results. Recognizing these common mistakes is the first step in preventing them in the future. By understanding where mistakes typically occur, you can improve your problem-solving skills and avoid unnecessary setbacks.
Misinterpreting the Problem
One of the most frequent mistakes is not fully understanding the question before attempting to solve it. Often, key details or conditions are overlooked, leading to incorrect conclusions. To avoid this, always take a moment to carefully read and analyze the problem. Look for all given information and ensure that you understand what is being asked before proceeding with any calculations.
Incorrect Application of Formulas
Another common issue arises when formulas are applied incorrectly. Sometimes, the wrong formula is used, or the necessary steps are skipped. This can easily happen when formulas are not fully understood or when assumptions are made. To prevent this, make sure to review and understand the formulas thoroughly before using them. Double-check each step to ensure you are following the correct procedure for solving the problem.
Strategies for Improving Your Test Performance
To perform well on assessments, it’s important to develop a focused approach that enhances both your knowledge and your problem-solving abilities. By employing effective study techniques and practicing regularly, you can boost your confidence and improve your results. These strategies will help you approach challenges with greater skill and accuracy.
Start by reviewing the core concepts regularly. Consistent revision helps reinforce your understanding, making it easier to recall the necessary information when needed. Additionally, practicing various problems allows you to familiarize yourself with different types of questions, ensuring you’re prepared for anything that comes up.
Another key strategy is to manage your time wisely during assessments. Prioritize questions based on their difficulty and allocate sufficient time for each. This will help you avoid spending too much time on one problem and ensure you address all aspects of the assessment effectively.
Additional Resources for Mastery
Expanding your understanding beyond the classroom is essential for mastering the material. There are numerous tools available that can provide extra practice, in-depth explanations, and varied perspectives on the topics at hand. Utilizing these resources will help solidify your knowledge and improve your problem-solving skills.
Online Learning Platforms

Many websites offer comprehensive tutorials, exercises, and videos on a wide range of topics. These platforms can cater to different learning styles, whether you prefer reading material, interactive quizzes, or video lectures.
- Khan Academy – Provides free lessons and exercises on various topics, including visual explanations.
- Coursera – Offers courses from universities and institutions that dive deeper into specific areas.
- Brilliant – A platform for problem-solving and active learning that enhances critical thinking.
Books and Study Guides

In addition to online resources, textbooks and study guides remain invaluable for reinforcing key concepts. Many books include practice problems with detailed solutions to help you understand each step.
- “Precalculus” by James Stewart – A comprehensive textbook covering essential concepts with worked examples.
- “Study Guide for Algebra” by Lial, Hornsby, and McGinnis – A detailed study guide offering clear explanations and exercises.