As we delve into Chapter 8 of our Geometry textbook, we are introduced to the fascinating world of right triangles and trigonometry. This chapter presents us with an opportunity to deepen our understanding of the relationships between the sides and angles of a right triangle and how they can be utilized to solve various problems.
Throughout this chapter, we will explore key concepts such as the Pythagorean Theorem, special right triangles, and the trigonometric ratios of sine, cosine, and tangent. These concepts not only provide us with a means to calculate missing side lengths or angles within right triangles, but they also have practical applications in fields such as engineering, architecture, and navigation.
By the end of Chapter 8, we will have a solid foundation in right triangles and trigonometry, enabling us to confidently tackle test questions on these topics. This article aims to provide answers to the chapter’s test questions, helping students assess their understanding and practice their problem-solving skills.
Chapter 8 Test: Right Triangles and Trigonometry Answers
In the Chapter 8 Test on Right Triangles and Trigonometry, students were asked to apply their understanding of right triangle concepts and trigonometric ratios to solve a variety of problems. This test aimed to assess their ability to calculate side lengths, angles, and missing information in right triangles using trigonometric functions.
The test consisted of multiple-choice questions, where students had to choose the correct answer among the given options. They also had to provide their reasoning and calculations to support their answers, showing their understanding of the concepts and principles involved in solving right triangle problems.
Some of the questions in the test focused on finding missing side lengths or angles in right triangles using trigonometric ratios such as sine, cosine, and tangent. Students were required to apply these ratios correctly and use inverse trigonometric functions when necessary to determine the angle measurements.
Other questions in the test involved solving real-world problems using right triangle trigonometry. For example, students might have been asked to determine the height of a tree, the length of a shadow, or the distance between two points based on given information and the principles of right triangle trigonometry.
The Chapter 8 Test: Right Triangles and Trigonometry aimed to assess students’ ability to apply their knowledge and skills in this area of geometry. By answering the questions correctly and providing appropriate justifications, students demonstrated their proficiency in using trigonometric functions and applying them to solve right triangle problems.
Overview

In geometry, Chapter 8 focuses on right triangles and trigonometry. This chapter explores the relationships between the sides and angles of right triangles, as well as the application of trigonometric ratios to solve problems involving right triangles.
The chapter begins by introducing the Pythagorean Theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This fundamental concept serves as the foundation for many of the topics covered in this chapter.
In addition to the Pythagorean Theorem, this chapter covers various trigonometric ratios such as sine, cosine, and tangent. These ratios relate the angles of a right triangle to the lengths of its sides. By applying these ratios, students can determine unknown side lengths or angles of right triangles.
To further reinforce the concepts, the chapter includes numerous examples and practice problems. These exercises allow students to apply the trigonometric principles learned to real-world scenarios, such as finding the height of a tree or the distance across a river.
Overall, Chapter 8 of the geometry curriculum provides a comprehensive understanding of right triangles and trigonometry. It equips students with the tools and knowledge necessary to solve problems involving right triangles, laying the groundwork for further exploration of geometry and trigonometry in higher levels of education.
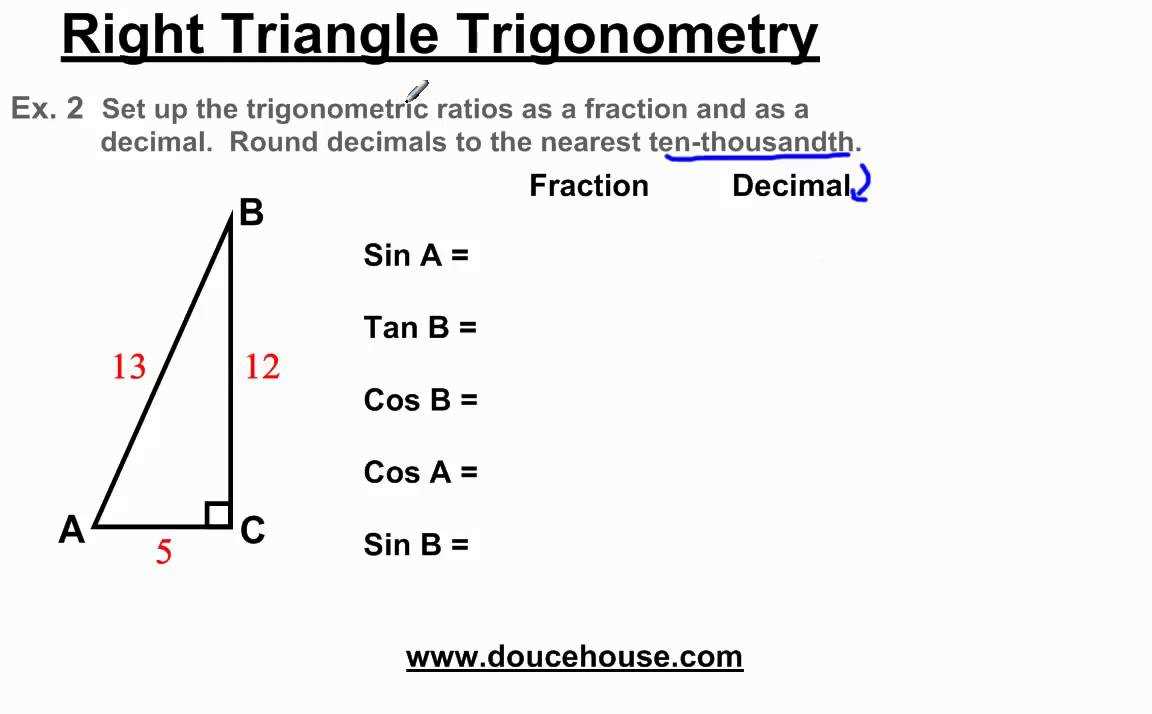
Question 1: Finding Missing Sides of Right Triangles

For example, let’s say we have a right triangle with an angle of 30 degrees and the length of the opposite side is 5 units. To find the length of the adjacent side, we can use the sine ratio. The sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. Therefore, we can set up the equation sin(30 degrees) = 5/hypotenuse. Solving for the hypotenuse, we find that the length of the hypotenuse is 10 units. Then, we can use the cosine ratio to find the length of the adjacent side, which is cos(30 degrees) = adjacent/10. Solving for the adjacent side, we find that the length is approximately 8.66 units.
In general, when solving for the missing sides of right triangles, we need to identify the given information (angle and length of a side) and determine which trigonometric ratio to use. Remember that sine is the ratio of the length of the opposite side to the hypotenuse, cosine is the ratio of the length of the adjacent side to the hypotenuse, and tangent is the ratio of the length of the opposite side to the adjacent side. By applying these ratios, we can solve for the missing sides of right triangles.
Question 2: Solving Right Triangles

When it comes to solving right triangles, there are various methods that can be used to find missing sides and angles. One common method is to use trigonometric ratios such as sine, cosine, and tangent.To solve a right triangle, we need to know at least one side length and one angle measurement. Once we have that information, we can use the trigonometric ratios to find the missing sides or angles. For example, if we know the length of one side and one angle, we can use the sine ratio to find the length of the opposite side. If we know the lengths of two sides, we can use the Pythagorean theorem to find the length of the third side.
In addition to trigonometry, we can also use special right triangle relationships to solve right triangles. For example, in a 45-45-90 triangle, the lengths of the legs are equal, and the length of the hypotenuse is equal to the length of a leg multiplied by the square root of 2. In a 30-60-90 triangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is equal to the length of the shorter leg multiplied by the square root of 3.
Overall, solving right triangles involves applying various mathematical concepts and formulas, including trigonometry and special right triangle relationships, to find missing sides and angles. It requires a good understanding of the properties and relationships of right triangles and the ability to use these properties and relationships to set up and solve equations.
Question 3: Special Right Triangles
In geometry, special right triangles are triangles with specific angles and side lengths that make calculations easier. There are two types of special right triangles: the 45-45-90 triangle and the 30-60-90 triangle.
The 45-45-90 Triangle
A 45-45-90 triangle is an isosceles right triangle, meaning it has two equal angles measuring 45 degrees and one right angle measuring 90 degrees. The side lengths of a 45-45-90 triangle are in a special ratio: 1:1:√2. This means that the lengths of the two legs are equal, and the length of the hypotenuse is equal to the length of a leg multiplied by √2.
For example, if one leg of a 45-45-90 triangle is 5 units, then the other leg is also 5 units, and the hypotenuse is 5√2 units. Similarly, if one leg is 7 units, then the other leg is also 7 units, and the hypotenuse is 7√2 units.
The 30-60-90 Triangle

A 30-60-90 triangle is a right triangle with angles measuring 30 degrees, 60 degrees, and 90 degrees. The side lengths of a 30-60-90 triangle are also in a special ratio: 1:√3:2. This means that the length of the shorter leg is equal to half the length of the hypotenuse, and the length of the longer leg is equal to the length of the shorter leg multiplied by √3.
For example, if the hypotenuse of a 30-60-90 triangle is 10 units, then the shorter leg is 5 units, and the longer leg is 5√3 units. Similarly, if the hypotenuse is 12 units, then the shorter leg is 6 units, and the longer leg is 6√3 units.
Understanding these special right triangles can help in solving various trigonometry problems and simplifying calculations involving right triangles. Knowing their side lengths and ratios can save time and make solving geometry problems more efficient and accurate.
Question 4: Trigonometric Ratios
The concept of trigonometric ratios is a fundamental part of solving problems involving right triangles and trigonometry. These ratios involve the relationships between the sides of a right triangle and the angles within the triangle. In question 4 of the Geometry chapter 8 test on right triangles and trigonometry, students are likely to encounter problems that require them to find the values of trigonometric ratios.
Trigonometric ratios, such as sine, cosine, and tangent, relate the angles of a right triangle to the sides of the triangle. The sine of an angle is defined as the ratio of the length of the side opposite the angle to the hypotenuse of the triangle. The cosine of an angle is defined as the ratio of the length of the adjacent side to the hypotenuse. Finally, the tangent of an angle is defined as the ratio of the length of the opposite side to the adjacent side.
To solve problems involving trigonometric ratios, students may need to use given information about the angles or sides of a right triangle to determine the values of these ratios. They may also need to use trigonometric identities to simplify expressions and find unknown values. It is important for students to understand the definitions of these ratios and how they relate to the sides of a right triangle, as well as how to apply them in various problem-solving situations.
By practicing and familiarizing themselves with the concepts and techniques of trigonometric ratios, students can improve their ability to solve problems related to right triangles and trigonometry. Being able to determine the values of these ratios is crucial for solving real-world problems in fields such as engineering, physics, and architecture. Understanding and mastering trigonometric ratios is essential for success in geometry and beyond.
Question 5: Using Trigonometry to Find Missing Angles
In this question, we are given a right triangle and we need to find the value of a missing angle using trigonometry.
To solve this problem, we can use the basic trigonometric ratios – sine, cosine, and tangent. These ratios relate the sides of a right triangle to its angles.
Let’s say we are given a right triangle ABC, where angle A is 90 degrees, side a is opposite angle A, side b is adjacent to angle A, and side c is the hypotenuse.
- The sine of angle A is equal to the ratio of the length of side a to the length of the hypotenuse: sin A = a/c
- The cosine of angle A is equal to the ratio of the length of side b to the length of the hypotenuse: cos A = b/c
- The tangent of angle A is equal to the ratio of the length of side a to the length of side b: tan A = a/b
Using these trigonometric ratios, we can find the value of the missing angle.
In conclusion, trigonometry provides us with a powerful tool to find missing angles in right triangles. By applying the sine, cosine, and tangent ratios, we can confidently solve problems involving right triangles and trigonometry.