
To solve problems involving right triangles, always apply the Pythagorean theorem when dealing with missing sides. For example, if you know two sides of a right triangle, you can quickly find the third side by using the formula a² + b² = c², where c represents the hypotenuse, and a and b are the legs of the triangle.
Practice calculating the area of polygons. For rectangles, simply multiply the length and width. In cases where you deal with circles, use the formula A = πr² to find the area. For trapezoids, apply the formula A = (b₁ + b₂)h / 2, where b₁ and b₂ are the lengths of the parallel sides, and h is the height.
For coordinate geometry, find the slope between two points using the formula m = (y₂ – y₁) / (x₂ – x₁). This is useful for determining whether two lines are parallel, perpendicular, or neither. If the slopes of two lines are negative reciprocals of each other, they are perpendicular. If they are equal, the lines are parallel.
Geometry Midterm Exam Review Answers
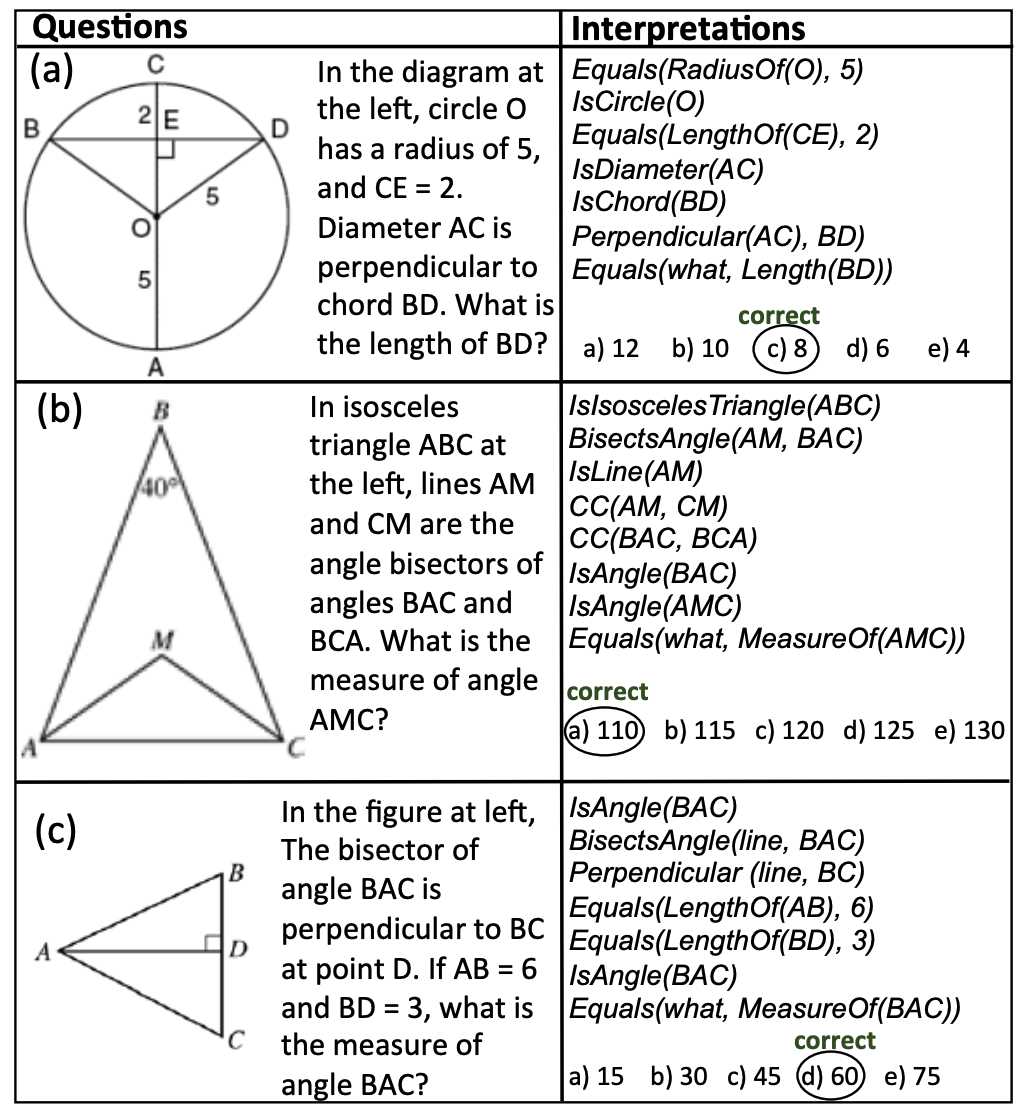
Understand key geometric principles to confidently tackle your midterm exam. Begin by reviewing basic properties of shapes and angles. For example, recall that the sum of interior angles of any triangle is 180°. Use this to find unknown angles when given two angles of a triangle.
Key Tips for Solving Problems

For problems involving right triangles, apply the Pythagorean theorem: a² + b² = c², where “a” and “b” are the legs, and “c” is the hypotenuse. This formula is critical when solving for missing sides in right-angled triangles.
Identifying Congruent and Similar Figures
When working with congruent triangles, remember that all corresponding sides and angles are equal. For similar triangles, the corresponding angles are equal, but the sides are proportional. Use the AA (Angle-Angle) similarity criterion to determine if two triangles are similar.
For quadrilaterals, pay attention to the properties of rectangles, squares, parallelograms, and trapezoids. For instance, the opposite sides of a parallelogram are congruent, and its angles are supplementary. The diagonals of a rectangle are equal in length.
In coordinate geometry, remember the distance formula to find the distance between two points: √((x₂ – x₁)² + (y₂ – y₁)²). Use the midpoint formula to find the center point between two coordinates: ((x₁ + x₂)/2, (y₁ + y₂)/2).
Lastly, focus on circle-related problems. The area of a circle is given by πr², and the circumference is 2πr. Understand how to apply these formulas for different scenarios, such as finding the area or arc length.
How to Solve Geometric Proofs: Step-by-Step Approach
Begin by reading the proof carefully and understanding what is given and what needs to be proved. Identify key geometric properties such as congruent angles, parallel lines, or the Pythagorean Theorem that may help. These properties often form the backbone of the argument.
Follow these steps to create a clear and logical proof:
- Identify Given Information: Highlight or list out all the information provided in the problem. This may include specific measurements, relationships, or angles.
- State What You Need to Prove: Make a clear note of the statement you are trying to prove. Keep it in mind as you proceed with the steps.
- Plan Your Approach: Think about geometric theorems or postulates that might be relevant, such as the properties of triangles, parallel lines, or circle theorems.
- Draw a Diagram: If a diagram is not provided, sketch one. Label it with all the given information and relationships that can help solve the proof.
- Apply Theorems and Postulates: Use known geometric principles step-by-step. For example, if two angles are vertical angles, state this and use the Vertical Angle Theorem. Each step should logically lead to the next.
- Justify Each Step: Provide a reason for each statement you make. Cite relevant postulates, theorems, or definitions that support each step of the proof.
- Conclude the Proof: Once you’ve reached the desired conclusion, summarize your findings. Ensure the proof covers all aspects of the problem without any gaps in logic.
Keep the structure of your proof simple and easy to follow. Avoid unnecessary steps that could complicate the reasoning. Practice solving various types of proofs to become more comfortable with the process.
Common Geometry Formulas You Need to Memorize for the Exam
Master these key formulas to tackle your geometry exam with confidence. Start with the area of a circle: A = πr², where “r” is the radius. Knowing this helps quickly calculate areas of circular shapes.
For triangles, use the formula A = 1/2 × base × height. It’s crucial for finding the area of any triangle, regardless of its type.
To calculate the perimeter of a rectangle, use P = 2(l + w), where “l” is length and “w” is width. This formula is handy for all four-sided shapes.
For squares, remember P = 4s, where “s” is the length of one side. It’s a simpler version of the rectangle perimeter formula.
For the area of a rectangle, A = l × w. It’s straightforward and applies to any rectangular figure.
The Pythagorean theorem is essential for right-angled triangles: a² + b² = c², where “a” and “b” are the legs, and “c” is the hypotenuse. This formula helps with distance and angle calculations.
For volume calculations, use V = l × w × h for rectangular prisms, where “l” is length, “w” is width, and “h” is height.
To find the surface area of a sphere, use A = 4πr². For the volume of a sphere, use V = 4/3 × πr³.
Lastly, for the perimeter of a circle (circumference), use C = 2πr. This is important for circular objects or any time you need to calculate distances around curves.
How to Tackle Word Problems Involving Geometry Concepts
First, identify key information in the problem. Read it carefully, and underline or highlight the values, shapes, and relationships mentioned. This gives you a clearer understanding of what’s provided and what needs to be found.
Next, visualize the problem. Draw the shapes or diagrams described in the question. Label all known values like sides, angles, and other relevant data. A well-drawn diagram can simplify complex word problems and provide a reference point throughout the solution process.
Apply Geometry Formulas
Once the diagram is ready, think about the formulas that relate to the problem. For instance, if the question involves areas or perimeters, recall the appropriate formulas for triangles, rectangles, circles, or other polygons. Use these formulas to express the unknowns in terms of known values from the problem.
Break Down the Problem
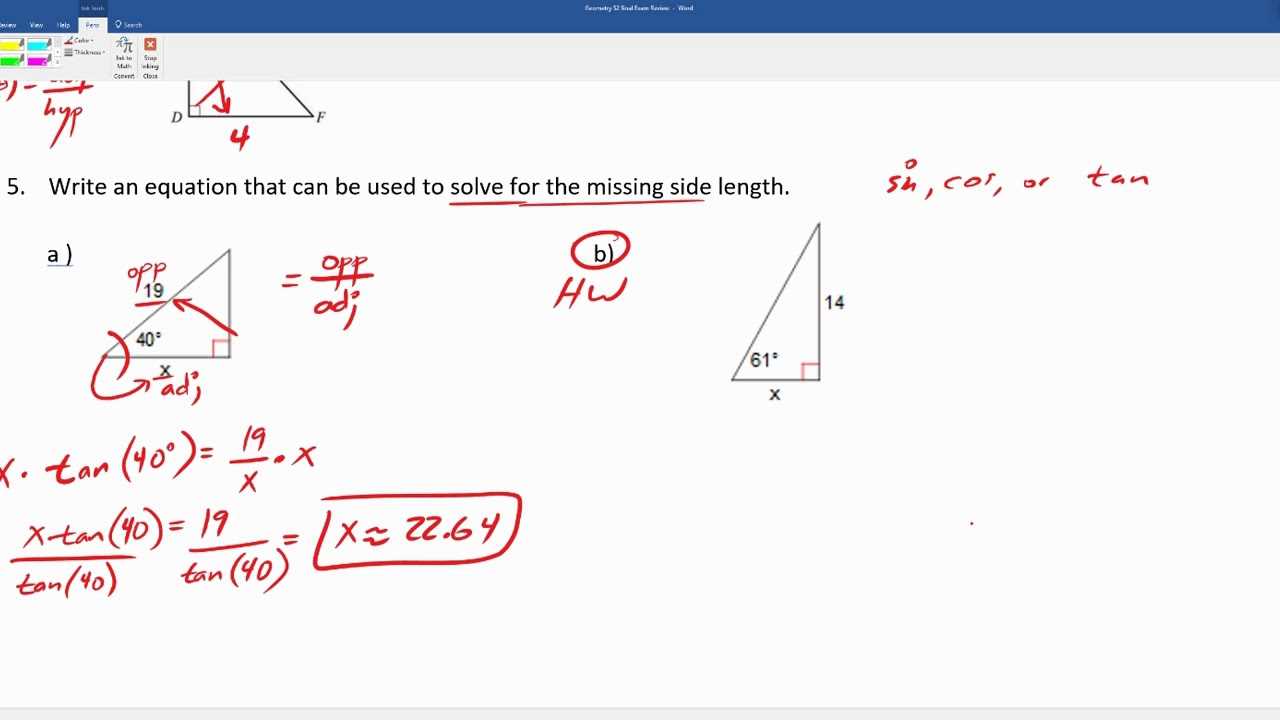
Break the problem into smaller steps. If a problem seems too complex, divide it into manageable parts. Solve one piece at a time, and connect each solution to move toward the final answer. Keep an eye on the specific geometry concepts being used–whether it’s the Pythagorean theorem, properties of circles, or properties of triangles–and apply them step by step.
Finally, double-check your work. Ensure the calculations are correct and all units match. Verifying each step avoids mistakes and ensures the solution is sound.