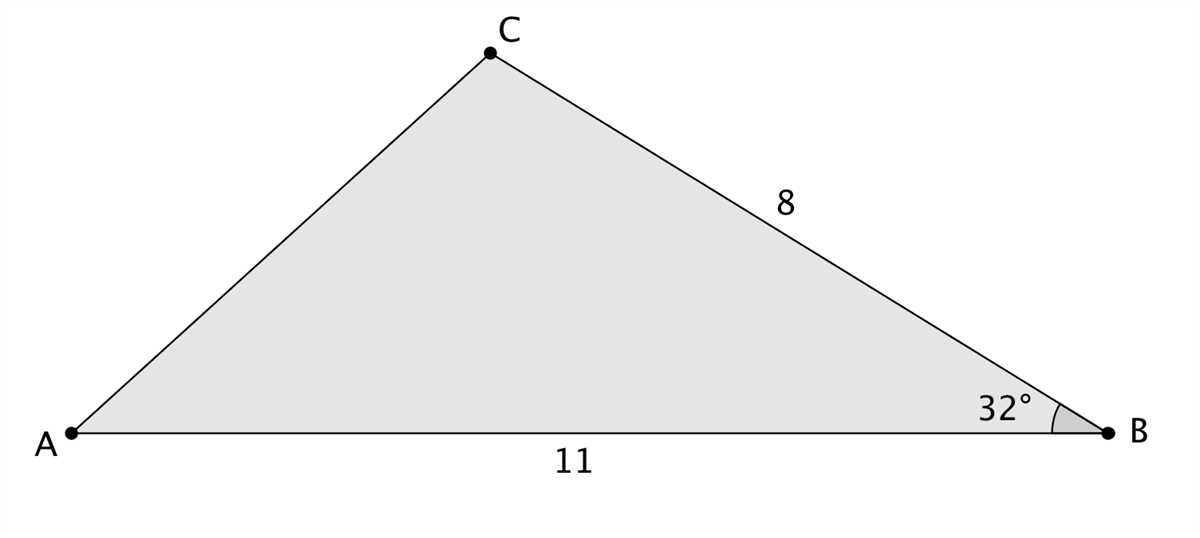
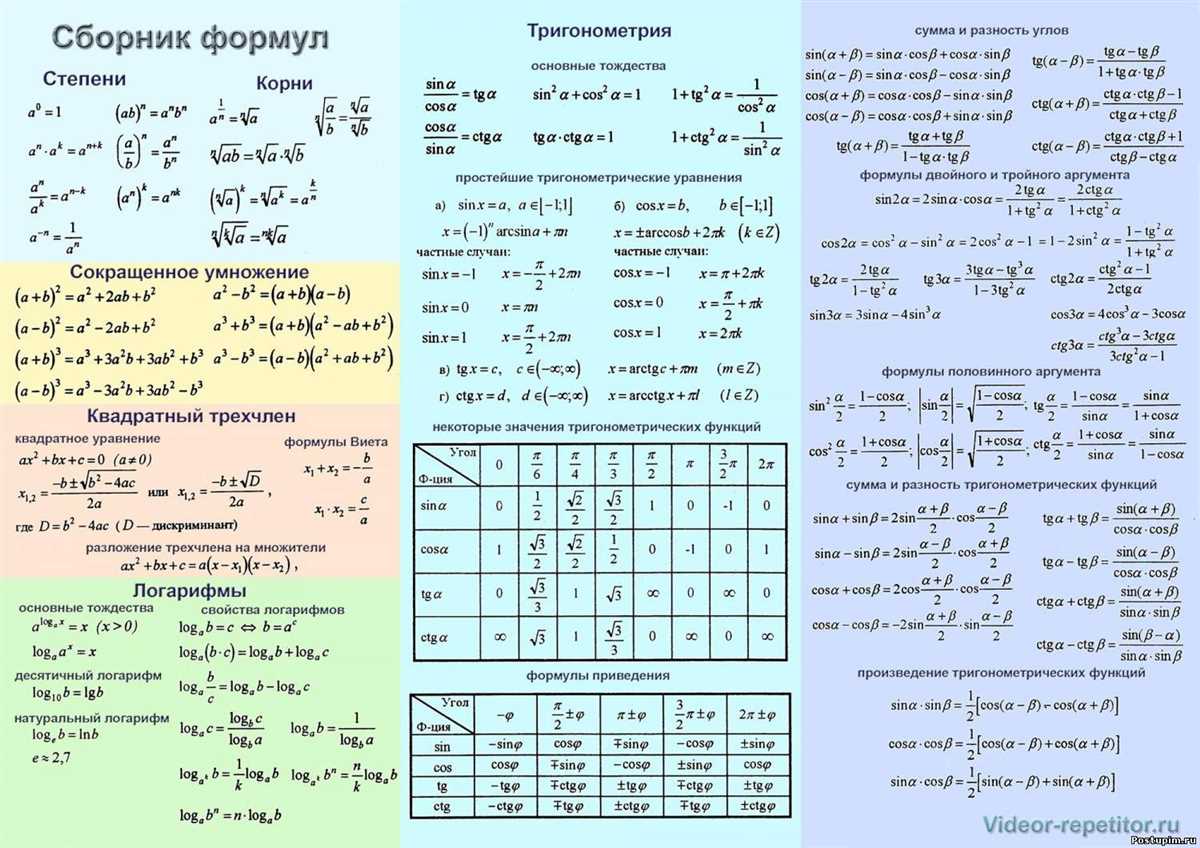
Welcome to the answer key for the geometry quiz on trigonometry! In this quiz, students were tested on their knowledge of various trigonometric concepts and formulas. Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is a fundamental topic in geometry and is often used in fields such as physics, engineering, and surveying.
The quiz consisted of multiple-choice and short answer questions that challenged students to apply their understanding of trigonometry to solve problems. Some of the key concepts covered in this quiz include the sine, cosine, and tangent functions, as well as the Pythagorean theorem and the unit circle. Students were also tested on their ability to use trigonometric ratios to find missing angles and sides of right triangles.
Now let’s take a look at the answer key for the quiz. This answer key will provide step-by-step solutions for each question, along with a detailed explanation of the reasoning behind each step. Whether you’re a student looking to check your answers or a teacher in need of a reference guide, this answer key will serve as a valuable resource for understanding the concepts and techniques used in trigonometry.
Geometry Quiz 8-2 Trigonometry Answer Key
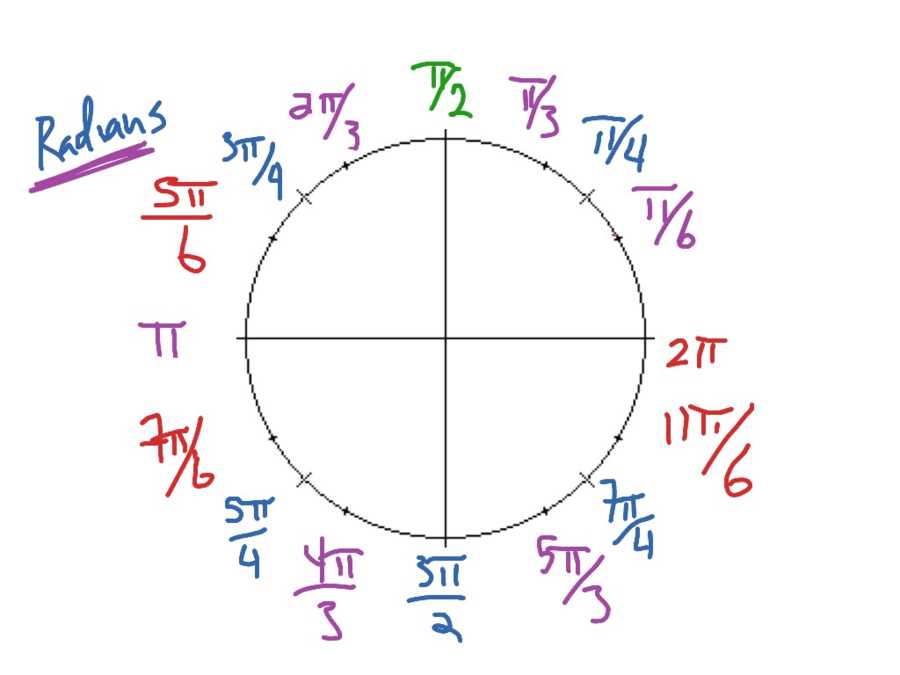
In the study of geometry, trigonometry plays a crucial role in understanding the relationships between angles and sides of triangles. It helps us solve various problems involving angles and distances, and it has applications in many fields such as engineering, physics, and architecture. In this quiz, you will be tested on your understanding of trigonometric concepts and the ability to apply them to solve problems.
The answer key for Geometry Quiz 8-2 Trigonometry provides the correct solutions for each question in the quiz. It serves as a guide for students to check their answers and identify any mistakes they may have made. The answer key also explains the step-by-step process for solving each problem, giving students a better understanding of the concepts involved.
Sample Answer Key:
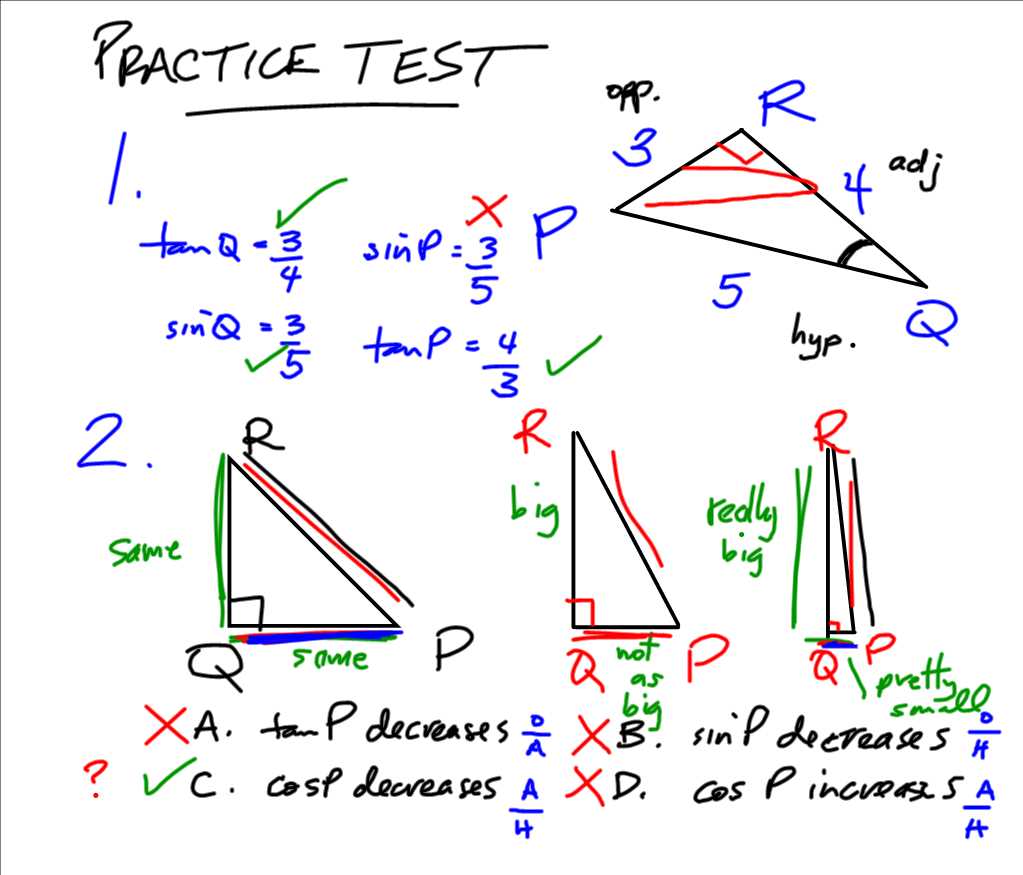
- Question 1: Find the value of the missing side in a right triangle with one angle measuring 30 degrees and the hypotenuse measuring 10 units.
Answer: The missing side can be found using the sine function: sin(30) = opposite/hypotenuse. Therefore, the missing side is 10 * sin(30) = 5 units. - Question 2: Determine the measure of angle θ in a right triangle with one leg measuring 8 units and the hypotenuse measuring 10 units.
Answer: The measure of angle θ can be found using the inverse cosine function: cos^(-1)(8/10) = 38.69 degrees. - Question 3: Calculate the area of a triangle with two sides measuring 4 units and 7 units, and the angle between them measuring 60 degrees.
Answer: The area of the triangle can be found using the formula: 1/2 * side1 * side2 * sin(angle) = 1/2 * 4 * 7 * sin(60) = 14 * √3 square units. - Question 4: Determine the length of the longest side in a triangle with angles measuring 45 degrees, 60 degrees, and 75 degrees.
Answer: The longest side can be found by comparing the lengths of the sides opposite the angles. The side opposite the 75-degree angle is the longest, so the length of the longest side is unknown.
By using the Geometry Quiz 8-2 Trigonometry Answer Key, students can evaluate their performance, learn from their mistakes, and improve their understanding of trigonometric concepts. Practicing with similar problems and seeking additional resources can further enhance their knowledge in this area of geometry.
Overview
In this geometry quiz on trigonometry, we will be testing your knowledge and understanding of various trigonometric concepts and formulas. Trigonometry is a branch of mathematics that deals with the relationships between angles and sides of triangles. It is widely used in various fields such as engineering, physics, and navigation.
Throughout this quiz, you will be presented with different types of problems involving trigonometric ratios, angles of elevation and depression, as well as applications of trigonometry in real-world scenarios. You will need to apply your understanding of trigonometric functions, such as sine, cosine, and tangent, to solve these problems.
- Trigonometric ratios: You will be asked to find the values of sine, cosine, and tangent for given angles.
- Angles of elevation and depression: You will be given information about the height and distance of an object and asked to find the angle of elevation or depression.
- Applications of trigonometry: You will be presented with real-world scenarios that involve trigonometric concepts, such as finding the height of a building or the distance between two objects.
To successfully complete this quiz, it is recommended that you have a solid understanding of basic trigonometric concepts, including the unit circle, right triangle trigonometry, and the trigonometric functions. You should also be familiar with the various properties and relationships of triangles, such as the Pythagorean theorem.
By the end of this quiz, you will have the opportunity to assess your understanding of trigonometry and identify any areas where you may need further practice or review. Good luck!
What is Trigonometry?

Trigonometry is a branch of mathematics that deals with the relationships and properties of triangles. It focuses on the study of angles, sides, and trigonometric functions, such as sine, cosine, and tangent. Trigonometry plays a crucial role in various fields, including physics, engineering, architecture, and navigation, as it provides tools for measuring and predicting the relationships between angles and distances in triangles.
To understand trigonometry, it is essential to grasp the concept of right triangles. A right triangle is a triangle that has one angle measuring 90 degrees (a right angle). Trigonometric functions are primarily based on the ratios of the sides of right triangles. The three main trigonometric functions are sine (sin), cosine (cos), and tangent (tan). These functions help in solving various problems involving angles and distances.
In trigonometry, the sine function (sin) relates the ratio of the length of the side opposite an angle to the length of the hypotenuse (the side opposite the right angle). The cosine function (cos) relates the ratio of the length of the side adjacent to an angle to the length of the hypotenuse. The tangent function (tan) relates the ratio of the length of the side opposite an angle to the length of the side adjacent to the angle.
The applications of trigonometry are vast. In physics, it is used to analyze the motion of objects, study waves and oscillations, and solve problems related to forces and vectors. In engineering and architecture, trigonometry helps in designing and constructing structures, calculating angles and distances, and determining the sizes of various components. In navigation, trigonometry is used to calculate the position and course of ships and aircraft.
Overall, trigonometry provides a powerful set of tools for analyzing and solving problems involving angles and distances. Its practical applications make it an essential branch of mathematics, indispensable in various disciplines that deal with spatial relationships and measurements.
Key Concepts
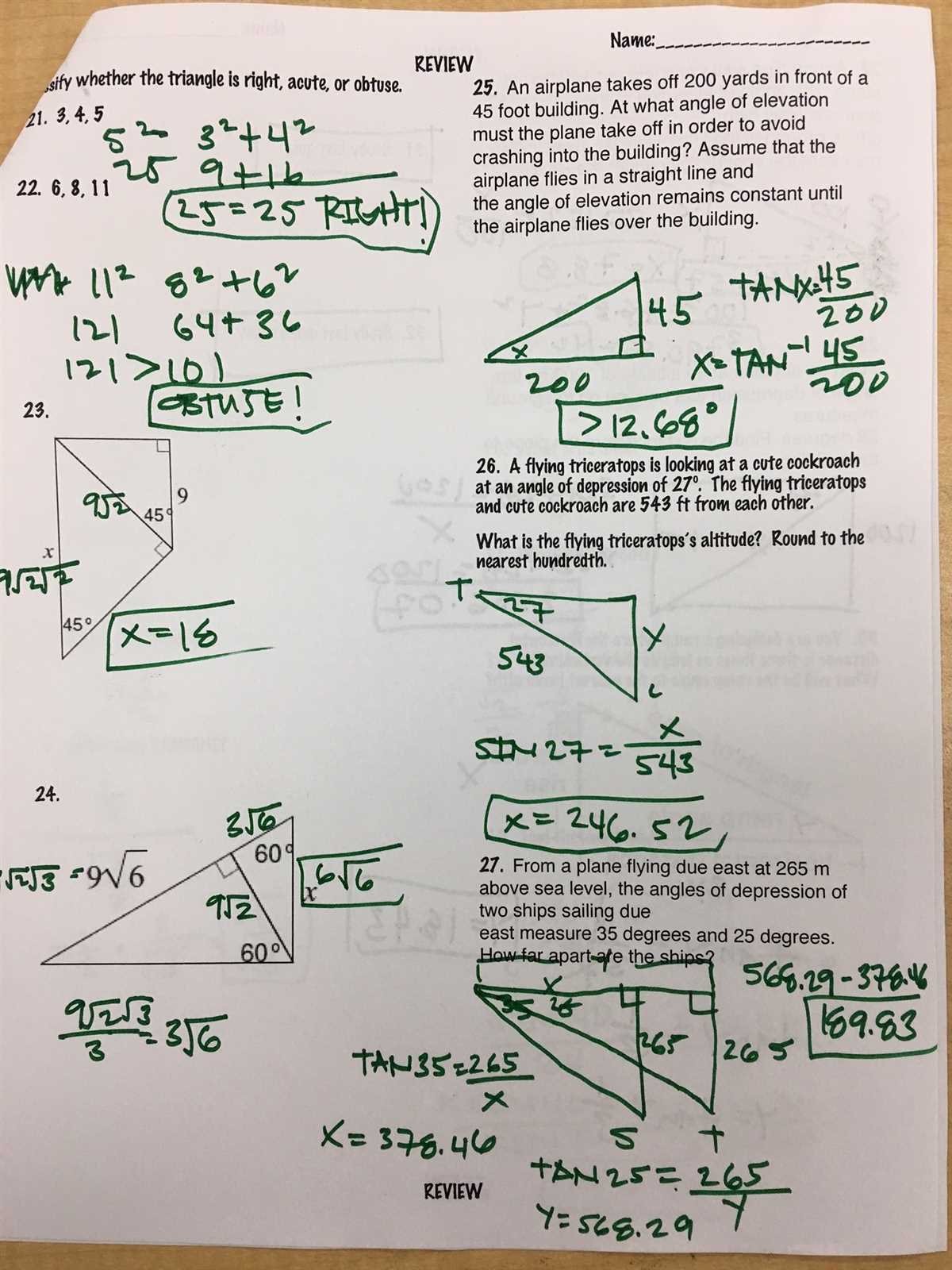
In the study of trigonometry, there are several key concepts that are important to understand. These concepts include the trigonometric ratios, special right triangles, the unit circle, and trigonometric identities.
Trigonometric Ratios: Trigonometric ratios are the ratios of the sides of a right triangle. The three primary trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). These ratios allow us to relate the angles of a triangle to the lengths of its sides.
Special Right Triangles: In geometry, there are two special right triangles that have easily identifiable ratios for their angles and sides. These triangles are the 45-45-90 triangle and the 30-60-90 triangle. Understanding the ratios within these triangles is crucial for solving trigonometric problems.
The Unit Circle: The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. It is used to understand the values of sine, cosine, and tangent for angles in standard position. The unit circle provides a way to express these trigonometric ratios as coordinates on the circle.
Trigonometric Identities: Trigonometric identities are equations that are true for all values of the variables that appear in them. These identities are used to simplify and solve trigonometric expressions and equations. Some common trigonometric identities include the Pythagorean identities and the reciprocal identities.
To have a strong understanding of trigonometry, it is important to grasp these key concepts and how they relate to each other. Mastery of these concepts will allow for success in solving trigonometry problems and applying trigonometry principles to various real-world scenarios.
How to Solve Trigonometry Problems
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is a fundamental concept that is used in various fields such as engineering, physics, and navigation. When faced with a trigonometry problem, it is important to approach it systematically and understand the key concepts involved.
1. Identify the given information: Read the problem carefully and identify the information given about angles and sides of the triangle. It is crucial to understand what is known and what needs to be found.
2. Choose the appropriate trigonometric ratio: Depending on the given information and what needs to be found, choose the appropriate trigonometric ratio – sine, cosine, or tangent. Recall that sine is the ratio of the opposite side to the hypotenuse, cosine is the ratio of the adjacent side to the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side.
3. Set up and solve the equation: Use the chosen trigonometric ratio to set up an equation based on the given information. Solve the equation for the unknown variable by isolating it on one side. This step may involve using algebraic operations such as addition, subtraction, multiplication, and division.
4. Check your answer: After finding the solution, it is essential to check if it makes sense in the context of the problem. Double-check the calculations and ensure that the units of measurement are consistent.
By following these steps and practicing regularly, you can improve your ability to solve trigonometry problems. Understanding the fundamental trigonometric ratios and their applications will enable you to tackle more complex problems with ease.
Sample Questions and Answers
Here are some sample questions and their corresponding answers for the Geometry quiz on trigonometry:
-
Question 1: Solve for the unknown side in a right triangle given that the adjacent side is 4 units and the angle of elevation is 30 degrees.
Answer: The unknown side can be found using the trigonometric ratio of cosine. Using the formula:
cos(angle) = adjacent/hypotenuse
Plugging in the known values, we get:
cos(30) = 4/hypotenuse
Solving for the hypotenuse, we find:
hypotenuse = 4/cos(30) = 4/0.866 = 4.618
Therefore, the unknown side is approximately 4.618 units.
-
Question 2: Find the value of the tangent of an angle in a right triangle if the opposite side is 3 units and the adjacent side is 5 units.
Answer: The value of the tangent can be determined using the trigonometric ratio of tangent. Using the formula:
tan(angle) = opposite/adjacent
Plugging in the given values, we have:
tan(angle) = 3/5
Therefore, the value of the tangent of the angle is 3/5.
These sample questions and answers illustrate the application of trigonometry in solving problems related to right triangles. By utilizing the appropriate trigonometric ratios, one can find missing side lengths or angle measures in a given triangle. Understanding and practicing trigonometry is crucial in solving more complex geometry problems and real-world applications.
Q&A:
What is a sample question?
A sample question is a question used as an example or a model to illustrate how to properly ask a question.
Why are sample questions important?
Sample questions are important because they provide a framework for understanding how to ask questions effectively. They help to guide individuals in formulating clear and concise inquiries.
Where can I find sample questions for a job interview?
Sample questions for a job interview can be found on various websites, career advice blogs, and in job interview preparation books. Additionally, many companies provide sample questions on their websites to help candidates prepare.
How do I create sample questions for a survey?
To create sample questions for a survey, first determine the goals and objectives of the survey. Then, brainstorm potential questions that will help gather the desired information. It can be beneficial to use a combination of open-ended and closed-ended questions to gather qualitative and quantitative data.
Can I use sample questions as they are or do I need to modify them?
Sample questions can be used as they are, but it is generally recommended to modify them to fit the specific context and purpose of your inquiry. This will help ensure that the questions accurately reflect what you are trying to learn or understand.