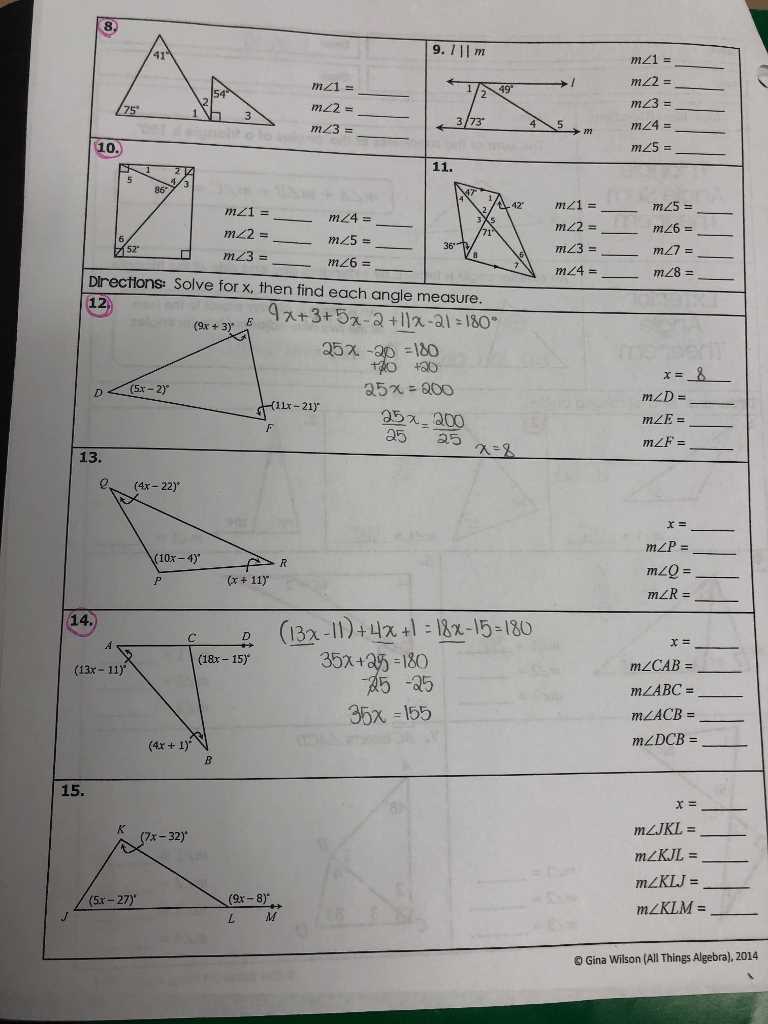
In 2014, Gina Wilson, an educator and math enthusiast, released a comprehensive algebra program called “All Things Algebra”. This program aimed to provide students with a thorough understanding of algebraic concepts and problem-solving techniques. One of the topics covered in the program was similar triangles, which are an important aspect of geometry.
Similar triangles are triangles that have the same shape but may differ in size. These triangles have proportional corresponding sides and congruent corresponding angles. Understanding the properties of similar triangles is essential for solving a variety of geometric problems, such as finding missing side lengths or angles.
In her program, Gina Wilson provided students with a set of exercises and problems to practice their skills in identifying and working with similar triangles. The “All Things Algebra” program also included answer keys for these exercises, allowing students to check their work and ensure they were on the right track.
By providing comprehensive answers to similar triangle problems, Gina Wilson aimed to support students in their learning process and help them develop a strong foundation in algebra and geometry. The “All Things Algebra” program became popular among teachers and students alike, as it offered a detailed and comprehensive approach to teaching and learning algebraic concepts.
Gina Wilson All Things Algebra 2014: Similar Triangles Answers
Gina Wilson All Things Algebra 2014 is a comprehensive educational resource developed by Gina Wilson. This particular resource focuses on the topic of similar triangles and provides answers to various problems and exercises related to this concept.
Similar triangles are a fundamental concept in geometry, which involves triangles that have the same shape, but may differ in size. These triangles have proportional side lengths and congruent corresponding angles.
The Gina Wilson All Things Algebra 2014 resource offers a variety of problems and exercises that allow students to practice identifying and working with similar triangles. The answers provided in this resource can serve as a helpful guide for students to check their work and gain a better understanding of the material.
By using this resource, students can strengthen their skills in solving problems involving similar triangles and gain confidence in their ability to tackle more complex geometry concepts. The Gina Wilson All Things Algebra 2014: Similar Triangles Answers resource provides the necessary tools for students to succeed in their geometry studies.
Overall, Gina Wilson All Things Algebra 2014: Similar Triangles Answers offers a valuable resource for students to improve their understanding and proficiency in working with similar triangles. With the provided answers, students can check their work and receive immediate feedback, allowing them to refine their problem-solving skills and deepen their knowledge of geometry.
Definition and Properties of Similar Triangles
Similar triangles are a special type of triangles that have the same shape but may differ in size. In other words, their corresponding angles are equal, and their corresponding sides are proportional. Understanding the properties of similar triangles is essential in various areas of mathematics, such as geometry and trigonometry.
Definition: Two triangles are similar if and only if their corresponding angles are congruent and their corresponding sides are in proportion. This can be denoted as ∆ABC ~ ∆XYZ, where ∆ represents a triangle and ~ represents similarity.
Properties of Similar Triangles:
- Angle-Angle (AA) Similarity: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. This can be stated as the AA similarity postulate.
- Side-Angle-Side (SAS) Similarity: If two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, then the triangles are similar.
- Side-Side-Side (SSS) Similarity: If the ratios of the corresponding sides of two triangles are equal, then the triangles are similar.
- Triangle Proportionality Theorem: If a line is parallel to one side of a triangle and intersects the other two sides, then it divides those sides proportionally.
- Triangle Midsegment Theorem: The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half its length. This can be used to prove similarity between triangles.
These properties of similar triangles allow us to establish relationships between corresponding angles and sides, and to solve problems involving proportions, ratios, and scale factors. They also serve as the foundation for further studies in trigonometry, where the concept of similarity is extensively used.
Methods for Proving Triangle Similarity
Triangle similarity is a fundamental concept in geometry that involves the comparison of two or more triangles to determine if they are similar. Similarity can be determined through various methods, which are essential tools in solving geometric problems and analyzing relationships between different figures.
One common method for proving triangle similarity is the Angle-Angle (AA) similarity theorem. According to this theorem, if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. This method relies on the fact that angles are a measure of the shape of the triangle, and if the angles of two triangles are equal, their shapes must also be equal, making them similar.
Another approach for proving triangle similarity is the Side-Angle-Side (SAS) similarity theorem. This theorem states that if two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, then the triangles are similar. This method combines both side length and angle measurement to determine if the triangles have proportional corresponding sides, indicating similarity.
In some cases, proving similarity may require more information, such as the Side-Side-Side (SSS) similarity theorem. This theorem states that if the corresponding sides of two triangles are proportional, then the triangles are similar. This method involves comparing the lengths of all three sides of the triangles to determine if they are in proportion.
Overall, these methods for proving triangle similarity provide a structured approach to analyzing and comparing triangles. By using different combinations of angle and side measurements, mathematicians and geometricians can determine the similarity of triangles and apply this knowledge to a wide range of geometric problems and constructions.
Applying Similar Triangles in Algebraic Equations
Similar triangles are an important concept in geometry that allows us to solve problems involving proportions and ratios. By identifying and applying the properties of similar triangles, we can find missing side lengths, angles, and solve algebraic equations.
One way we can apply similar triangles in algebraic equations is by using the concept of proportionality. When two triangles are similar, their corresponding side lengths are proportional. This means that we can set up algebraic equations to solve for unknown values.
Example:
Let’s say we have two similar triangles, triangle ABC and triangle DEF. If the ratio of their corresponding side lengths is 2:3, and we know the length of side AB is 4, we can set up the following equation:
- AB/DE = BC/EF = AC/DF = 2/3
Since we know the length of AB is 4, we can substitute this value into the equation:
- 4/DE = BC/EF = AC/DF = 2/3
Now we can solve for the length of DE by cross-multiplying:
- 2 * DE = 4 * 3
- 2DE = 12
- DE = 6
Therefore, the length of DE in triangle DEF is 6.
By using similar triangles and proportionality, we can solve algebraic equations involving multiple unknowns and find missing values. This concept is often used in various fields such as engineering, architecture, and physics to solve real-world problems involving similar shapes and proportions.
Using Similar Triangles to Solve Real-World Problems

In the world of mathematics, the concept of similar triangles plays a crucial role in solving real-world problems. An understanding of the properties of similar triangles allows us to make accurate measurements and calculations in various practical situations.
Similar triangles are polygons that have the same shape but may differ in size. They have corresponding angles that are equal and corresponding sides that are proportional. By identifying and utilizing these similarities, we can apply the principles of similar triangles to find unknown measurements or solve complex problems.
One practical application of similar triangles is in the field of surveying. Surveyors use this concept to determine the height or distance of a tall object, such as a building or a tree, by comparing its shadow to the length of a known object’s shadow. By creating similar triangles using the height or distance of the known object and its corresponding shadow length, surveyors can calculate the unknown measurements using proportions.
Another real-world situation where similar triangles are used is in navigation. Pilots and sailors often rely on similar triangles to estimate distances or heights. By comparing the angular size of an object, such as a lighthouse or a mountain, to its known height, they can determine the distance to the object using the principles of similar triangles.
Similar triangles also come into play in architectural and engineering designs. Architects use them to scale down models and create accurate blueprints. Engineers use similar triangles to calculate the dimensions of structures, such as bridges or buildings, by measuring known lengths and angles and using them to find the corresponding unknown measurements.
In conclusion, the concept of similar triangles has a wide range of real-world applications. By using the properties of similar triangles, we can solve problems in surveying, navigation, architecture, and engineering. This mathematical concept enhances our understanding of the physical world and enables us to make accurate calculations in various practical situations.
Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key
In the study of geometry, similar triangles are an important concept to understand. Gina Wilson, a renowned mathematics teacher and curriculum developer, has created the “All Things Algebra” series, which includes a comprehensive guide to solving similar triangle problems.
The answer key from Gina Wilson’s All Things Algebra 2014 Similar Triangles is a valuable resource for students and teachers alike. It provides step-by-step solutions to all the problems presented in the textbook, allowing students to check their work and gain a better understanding of the concepts.
The answer key is organized by chapter and section, making it easy to locate specific problems and solutions. Wilson provides clear explanations and diagrams to help students visualize the solutions and grasp the underlying concepts.
By using the answer key, students can practice solving similar triangle problems and assess their understanding of the material. Teachers can also use it as a tool for grading assignments and providing feedback to students.
In conclusion, Gina Wilson’s All Things Algebra 2014 Similar Triangles answer key is a helpful resource for both students and teachers. It allows students to check their work, practice solving problems, and deepen their understanding of similar triangles. For teachers, it can serve as a grading tool and a source of additional explanations and examples.
Q&A:
What is Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key?
Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key is a set of answers to the questions and problems found in the 2014 edition of Gina Wilson’s All Things Algebra book on similar triangles.
Where can I find Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key?
You can find Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key in the back of the 2014 edition of Gina Wilson’s All Things Algebra book on similar triangles.
How can I use Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key?
You can use Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key to check your answers and to help you understand the process and steps needed to solve similar triangles problems.
Can I rely solely on Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key to study for a similar triangles test?
No, it’s not recommended to rely solely on Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key. It’s important to also understand the concepts and principles behind similar triangles and practice solving problems on your own.
Is Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key still relevant in 2021?
Although the 2014 edition of Gina Wilson All Things Algebra book on similar triangles is a bit older, the concepts and principles of similar triangles have not changed. Therefore, Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key can still be relevant in 2021.
What is the Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key?
The Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key is a document that contains the answers to the questions and exercises in the Gina Wilson All Things Algebra workbook on the topic of similar triangles. It is used as a resource for students and teachers to check their work and for studying purposes.
Where can I find the Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key?
The Gina Wilson All Things Algebra 2014 Similar Triangles Answer Key can be found in the Gina Wilson All Things Algebra workbook itself. It is usually located towards the end of the book, after all the questions and exercises on the topic of similar triangles. Alternatively, it may also be available as a separate document or resource provided by the publisher. If you are unable to find it, you can try contacting the publisher or your teacher for assistance.