Kepler’s laws of planetary motion have captivated astronomers and physicists for centuries. These laws, formulated by the German mathematician and astronomer Johannes Kepler in the early 17th century, revolutionized our understanding of how celestial bodies move within the solar system.
In this article, we will delve into the Kepler’s laws gizmo answers, exploring the intricate details of these laws and how they can be applied to solve various celestial motion problems. Whether you’re a student studying astronomy or simply an enthusiast looking to expand your knowledge, this comprehensive guide will provide you with the answers you need.
The Kepler’s laws gizmo is an online interactive tool that allows users to explore the three laws in a practical and visual manner. Through this gizmo, users can simulate different scenarios, adjust parameters, and observe the effects on planetary orbits, helping to solidify their understanding of Kepler’s laws.
From determining the shape of planetary orbits to understanding the relationship between distance and orbital period, the gizmo provides a platform for students and learners of all levels to experiment and explore the intricacies of Kepler’s laws.
Understanding Kepler’s Laws Gizmo Answers
The Kepler’s Laws Gizmo is a powerful tool that helps students understand and visualize the three laws formulated by the famous astronomer Johannes Kepler. These laws describe the motion and behavior of planets in our solar system. By using the Gizmo, students can explore these laws and gain a deeper understanding of how they govern planetary motion.
One of the key features of the Kepler’s Laws Gizmo is the ability to simulate and observe the motion of planets in orbit around a star. This allows students to see firsthand how the laws of planetary motion apply to different scenarios. By adjusting parameters such as planet mass and distance from the star, students can see the effects on the shape and size of the orbit.
The Gizmo also provides answers to specific questions related to Kepler’s laws. For example, students can investigate how changing the eccentricity of an orbit affects the speed of the planet at different points along its orbit. They can also explore how the period of a planet’s orbit changes as its distance from the star is altered. These answers provide valuable insights into the relationship between the variables involved in Kepler’s laws.
Furthermore, the Gizmo enables students to compare and contrast the behavior of different planets in our solar system. They can observe how the inner planets, such as Mercury and Venus, have shorter orbital periods and smaller orbits compared to the outer planets like Jupiter and Saturn. This helps students see the patterns and principles behind Kepler’s laws in action.
In summary, the Kepler’s Laws Gizmo is an interactive and educational tool that allows students to understand and explore the principles of planetary motion. By using the Gizmo, students can gain a deeper appreciation for the work of Johannes Kepler and the laws that govern the movement of the planets in our solar system.
Exploring the First Law: The Law of Ellipses
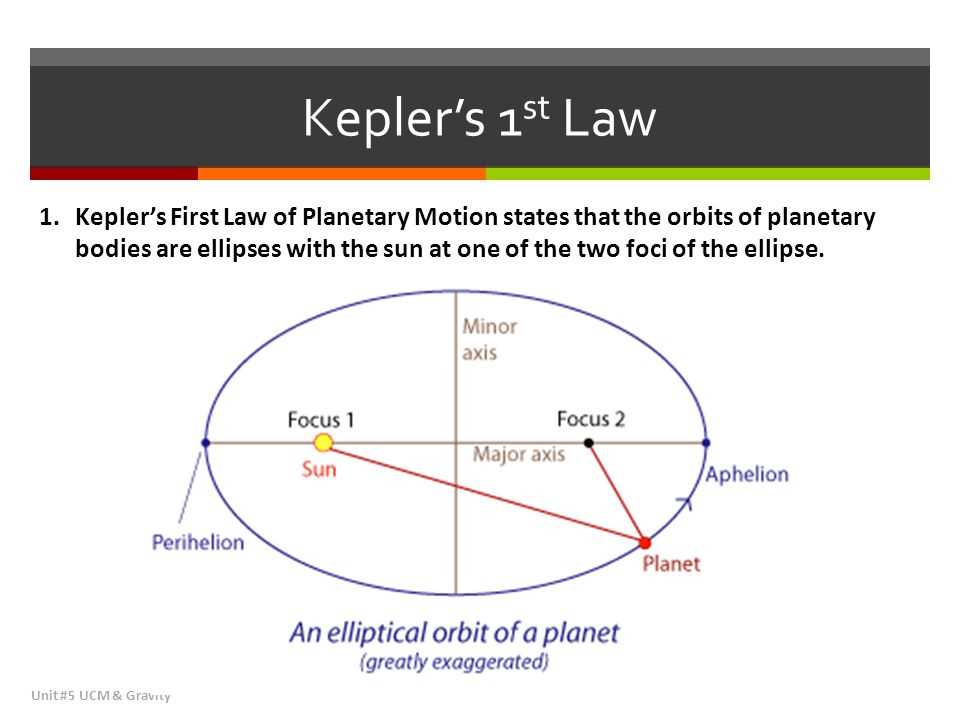
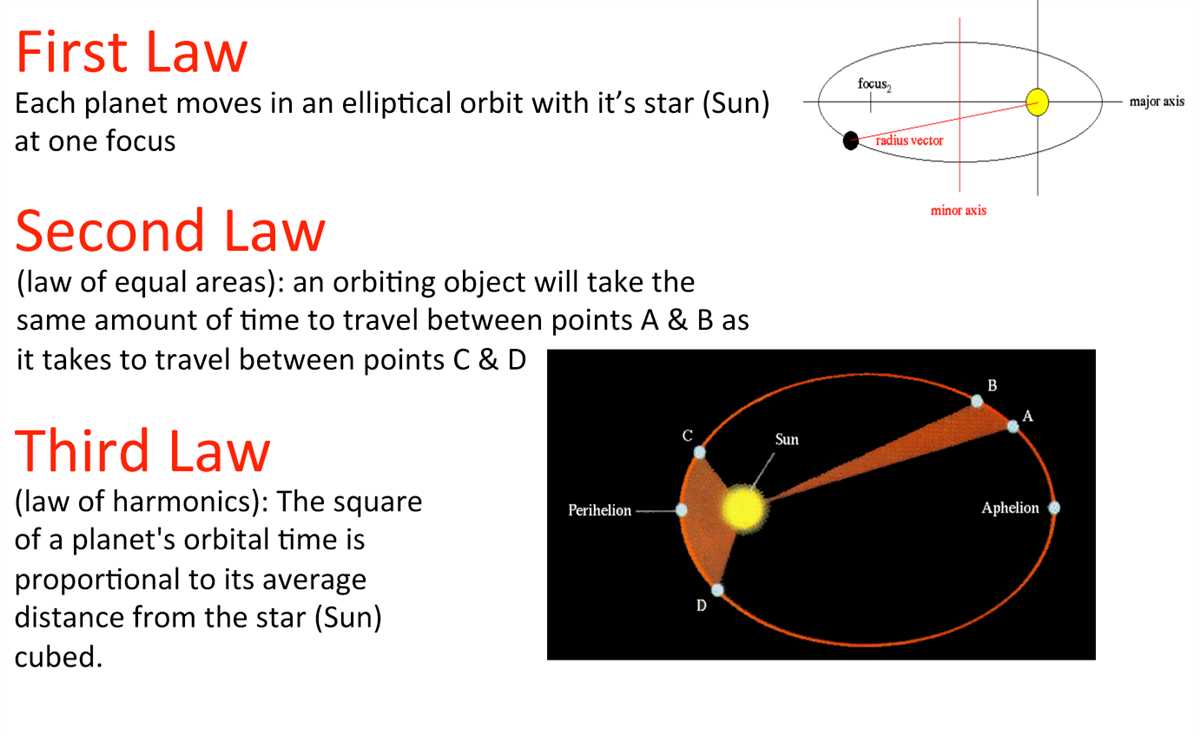
The Law of Ellipses, also known as Kepler’s First Law, is one of the three fundamental laws of planetary motion discovered by the astronomer Johannes Kepler in the early 17th century. This law describes the shape of the orbits of planets around the sun.
According to the Law of Ellipses, the path of each planet around the sun is an ellipse with the sun at one of the foci. An ellipse is a type of closed curve with a characteristic elongated shape, resembling a flattened circle. The sun occupies one of the two foci of the ellipse, while the planet follows the path of the ellipse as it orbits around the sun.
To better understand the concept of ellipses and how they relate to planetary motion, let’s consider some key terms. The major axis of an ellipse is the longest diameter that passes through the center of the ellipse. The minor axis is the shortest diameter that also passes through the center. The distance from the center of the ellipse to either focus is called the semi-major axis. The eccentricity of an ellipse measures how elongated or flattened it is, with a value of 0 indicating a perfect circle and a value approaching 1 indicating a highly elongated ellipse.
Kepler’s First Law revolutionized our understanding of celestial motion by challenging the widely accepted belief that planetary orbits were perfect circles. This law brought about a fundamental shift in our understanding of planetary motion and paved the way for Newton’s laws of motion and the law of universal gravitation.
Unraveling the Second Law: The Law of Equal Areas
The second law of planetary motion, also known as the law of equal areas, is one of the three laws formulated by Johannes Kepler to describe the motion of planets around the sun. This law states that the line connecting a planet to the sun sweeps out equal areas in equal time intervals. In other words, the planet moves faster when it is closer to the sun and slower when it is farther away.
This law can be better understood by considering the concept of angular momentum. Angular momentum is the property of a rotating object that determines how it resists changes to its rotation. In the context of planetary motion, the planet’s orbital angular momentum is conserved, meaning it remains constant as the planet moves around its orbit.
When the planet is closer to the sun, its velocity increases, and as a result, its angular momentum also increases. This increase in angular momentum is compensated by a decrease in the planet’s orbital radius, as the equal areas law dictates. Conversely, when the planet is farther from the sun, its velocity decreases, reducing its angular momentum. To maintain conservation of angular momentum, the planet’s orbital radius must increase.
This relationship between velocity, angular momentum, and orbital radius helps to explain why planets move faster when they are closer to the sun and slower when they are farther away. By understanding this relationship, scientists have been able to accurately predict and model the motion of planets in our solar system, as well as other celestial bodies.
Investigating the Third Law: The Law of Periods
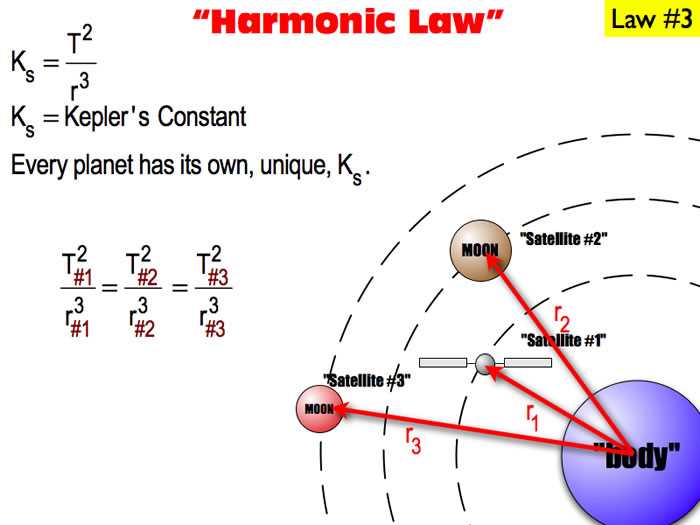
The Law of Periods, also known as Kepler’s Third Law, states that the square of the orbital period of a planet is directly proportional to the cube of its average distance from the sun. This law is based on Johannes Kepler’s observations of the planets in our solar system and is a fundamental principle in understanding celestial motion.
To investigate the Law of Periods, scientists use the Kepler’s laws gizmo, a simulation tool that allows them to study the relationship between a planet’s orbital period and its distance from the sun. By manipulating the settings and variables in the gizmo, researchers can gather data and analyze the patterns to validate Kepler’s Third Law.
Data Collection
Using the Kepler’s laws gizmo, scientists can record the orbital period and average distance from the sun of multiple planets. They can then calculate the square of the orbital period and the cube of the average distance for each planet. This data is essential for verifying Kepler’s Third Law and understanding the relationship between the two variables.
Data Analysis and Results

After collecting the data, scientists can plot the square of the orbital period against the cube of the average distance on a graph. If Kepler’s Third Law holds true, the data points should fall on a straight line. Any deviation from a straight line could indicate errors in measurement or other factors influencing the motion of the planets.
By analyzing the graph, scientists can determine the proportionality constant relating the square of the orbital period to the cube of the average distance. This constant is crucial for calculating the orbital period of planets that have not been directly observed and for predicting the behavior of celestial bodies in other solar systems.
- Conclusion: The investigation of the Law of Periods using the Kepler’s laws gizmo allows scientists to validate Kepler’s Third Law and gain a deeper understanding of the motion of planets in our solar system. By analyzing the data collected and plotting it on a graph, researchers can confirm the proportional relationship between the orbital period and average distance and calculate the necessary constants for further astronomical calculations.
Discovering Gizmo Answers to Kepler’s Laws
Kepler’s laws are fundamental principles in the field of astronomy that describe the motion of planets around the Sun. They were derived by the renowned astronomer Johannes Kepler in the 17th century, and have since been instrumental in our understanding of the solar system. The Kepler’s Laws Gizmo is a powerful tool for exploring and understanding these laws, allowing students and researchers to simulate and visualize planetary motion.
The Gizmo provides interactive simulations and exercises that guide users through the discovery of Kepler’s laws. Through these exercises, users can observe the orbital paths of planets, measure the distance traveled by planets in different time intervals, and analyze the relationship between a planet’s orbital period and its distance from the Sun. By manipulating variables such as the eccentricity of the planet’s orbit and the mass of the central body, users can investigate the effects of these factors on planetary motion.
One of the key features of the Gizmo is the ability to visualize Kepler’s laws in action. Users can observe how a planet’s speed changes depending on its position in its orbit, which is determined by the law of equal areas. They can also explore the concept of orbital eccentricity and observe how it affects a planet’s distance from the Sun at different points in its orbit. Additionally, the Gizmo allows users to compare the orbital periods of different planets and discover the relationship between a planet’s distance from the Sun and its orbital period.
In conclusion, the Kepler’s Laws Gizmo provides an engaging and interactive platform for discovering the answers to Kepler’s laws. By simulating and manipulating planetary motion, users can gain a deeper understanding of these fundamental principles and their implications for our understanding of the solar system. Whether used in a classroom setting or for independent research, the Gizmo offers an effective way to explore and comprehend the laws governing the motion of planets around the Sun.
Applying Kepler’s Laws in Real-life Scenarios
The laws discovered by Johannes Kepler have had a profound impact on our understanding of the motion of celestial bodies in space. However, these laws are not limited to theoretical calculations and observations. They can also be applied to real-life scenarios, helping us to solve practical problems and make important decisions.
1. Orbital Mechanics: Kepler’s laws are crucial for understanding and predicting the movement of satellites and spacecraft in orbit around the Earth or other celestial bodies. By applying Kepler’s laws, engineers can determine the optimal trajectory and timing for launch, calculate the required velocity and altitude for a stable orbit, and plan maneuvers to change orbits or rendezvous with other spacecraft.
2. Planetary Exploration: Kepler’s laws guide missions to explore other planets and their moons. By studying the motions of these celestial bodies and applying Kepler’s laws, scientists can plan spacecraft trajectories to reach their destinations efficiently and accurately. This helps in conducting scientific experiments, collecting data, and exploring the mysteries of the universe.
3. Spacecraft Navigation: Kepler’s laws are also used for spacecraft navigation, ensuring accurate positioning and course corrections. By analyzing the orbital elements of a spacecraft and considering the gravitational forces of celestial bodies, mission controllers can calculate the spacecraft’s position, velocity, and trajectory. This helps in maintaining a desired orbit, avoiding potential collisions, and successfully completing missions.
4. Astrodynamic Engineering: Kepler’s laws are fundamental for astrodynamic engineering, which involves the design and analysis of space missions. By applying Kepler’s laws, engineers can simulate and predict the behavior of spacecraft and satellites, calculate the required propulsion and power systems, and optimize mission parameters. This helps in designing efficient and cost-effective space missions.
In conclusion, Kepler’s laws have far-reaching applications beyond theoretical astronomy. They are invaluable tools for space exploration, spacecraft navigation, and engineering. By understanding and applying these laws, scientists and engineers can make accurate predictions, plan missions, and explore the vastness of space.