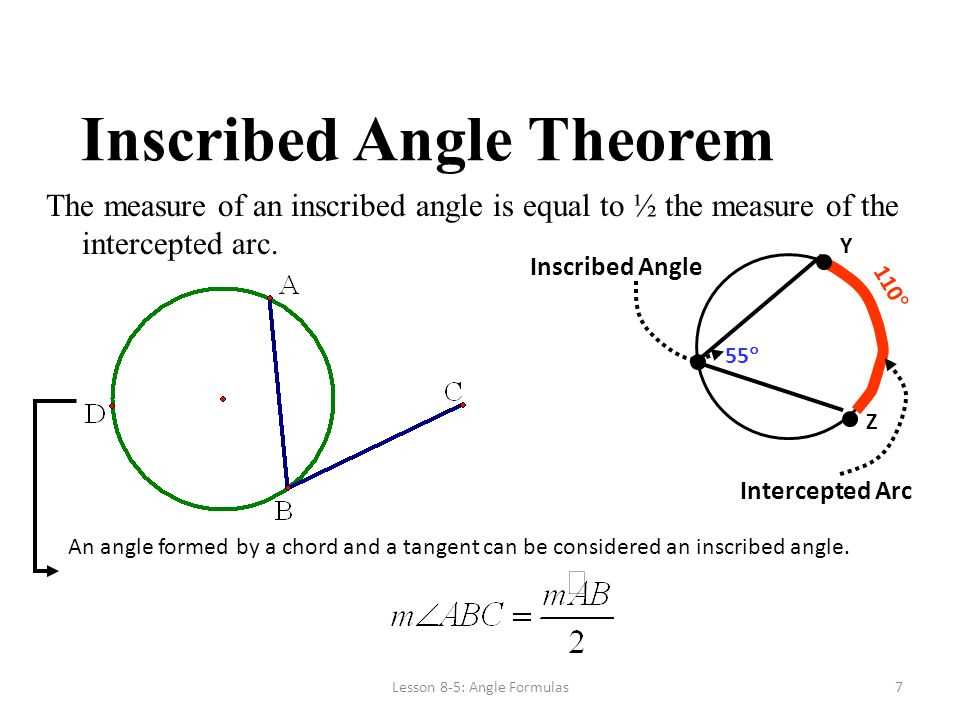
Inscribed angles are angles formed by two chords in a circle that have their endpoints on the circle. These angles can be used to solve various problems involving the relationships between chords, arcs, and central angles in a circle.
In this lesson, we will be practicing solving problems involving inscribed angles. The questions in Practice A will cover concepts such as the relationship between an inscribed angle and its intercepted arc, the relationship between inscribed angles and central angles, and the properties of tangent lines and circles.
By working through the practice problems and understanding the concepts behind them, you will be able to apply this knowledge to solve more complex problems involving inscribed angles. This will not only help you in your math studies but also in real-life situations that involve circles and angles.
Remember to use the given information and apply the relevant theorems and properties to solve each problem. If you are unsure about any concept or need further clarification, refer back to the lesson materials and practice examples. Use the provided answers to check your work and identify any areas where you may need further practice or review.
What are inscribed angles and why are they important?
When a circle is inscribed in a polygon, it means that all the vertices of the polygon touch the circle. An inscribed angle is an angle formed by two chords within a circle where the vertex is on the circle itself. It is important to study and understand inscribed angles because they have several properties and applications in geometry.
One important property of inscribed angles is that their measure is half the measure of the intercepted arc. This relationship can be used to find missing angle measures in a circle or to prove geometric theorems. In addition, inscribed angles can help determine the relationships between different angles and arcs within a circle.
Another reason why inscribed angles are important is their connection to the concept of a central angle. A central angle is an angle whose vertex is at the center of a circle and whose sides intersect the circle. Inscribed angles subtend the same arc as their corresponding central angles. This relationship is useful in solving problems involving angles and arcs in circles.
Inscribed angles are also crucial in solving real-world problems that involve circular objects or motions. They can be used to calculate distances, angles, or areas in various fields such as engineering, architecture, and physics.
In conclusion, understanding inscribed angles is vital for studying geometry and solving problems related to circles. Their properties and relationships with arcs and central angles make them an important tool in various mathematical and practical applications.
The Relationship Between Inscribed Angles and Central Angles
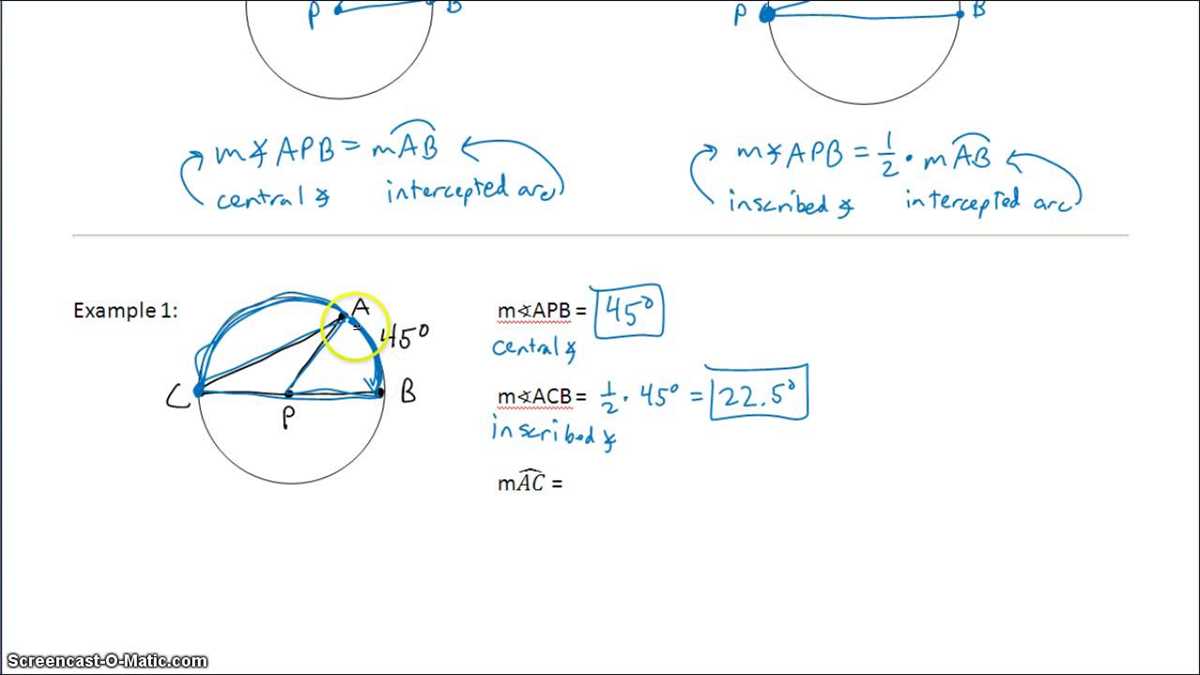
In geometry, a central angle is an angle whose vertex is at the center of a circle and its sides pass through two points on the circle. On the other hand, an inscribed angle is an angle whose vertex is on the circle and its sides intersect the circle at two different points.
There is a unique relationship between inscribed angles and central angles in a circle. The measure of an inscribed angle is equal to half the measure of its intercepted arc. This means that if we know the measure of the intercepted arc, we can find the measure of the corresponding inscribed angle by dividing it by 2. Conversely, if we know the measure of an inscribed angle, we can find the measure of its intercepted arc by multiplying the angle measure by 2.
This relationship is derived from the fact that the sum of the measures of the angles in a triangle is always 180 degrees. In the case of a triangle formed by a central angle, an inscribed angle, and the intercepted arc, the central angle and the inscribed angle together form a linear pair, which means they add up to 180 degrees. Therefore, the measure of the inscribed angle is half the measure of the intercepted arc.
This relationship is useful in various geometric proofs and calculations involving circles. It allows us to find missing angles and measure arcs based on the information given about inscribed angles or central angles. By understanding this relationship, we can better understand and solve problems related to circles and their properties.
Summary:

- A central angle is an angle whose vertex is at the center of a circle, while an inscribed angle is an angle whose vertex is on the circle.
- The measure of an inscribed angle is equal to half the measure of its intercepted arc.
- The relationship between inscribed angles and central angles is based on the fact that the sum of the measures of the angles in a triangle is always 180 degrees.
- This relationship is useful in solving problems and proofs involving circles.
How to Find the Measure of an Inscribed Angle
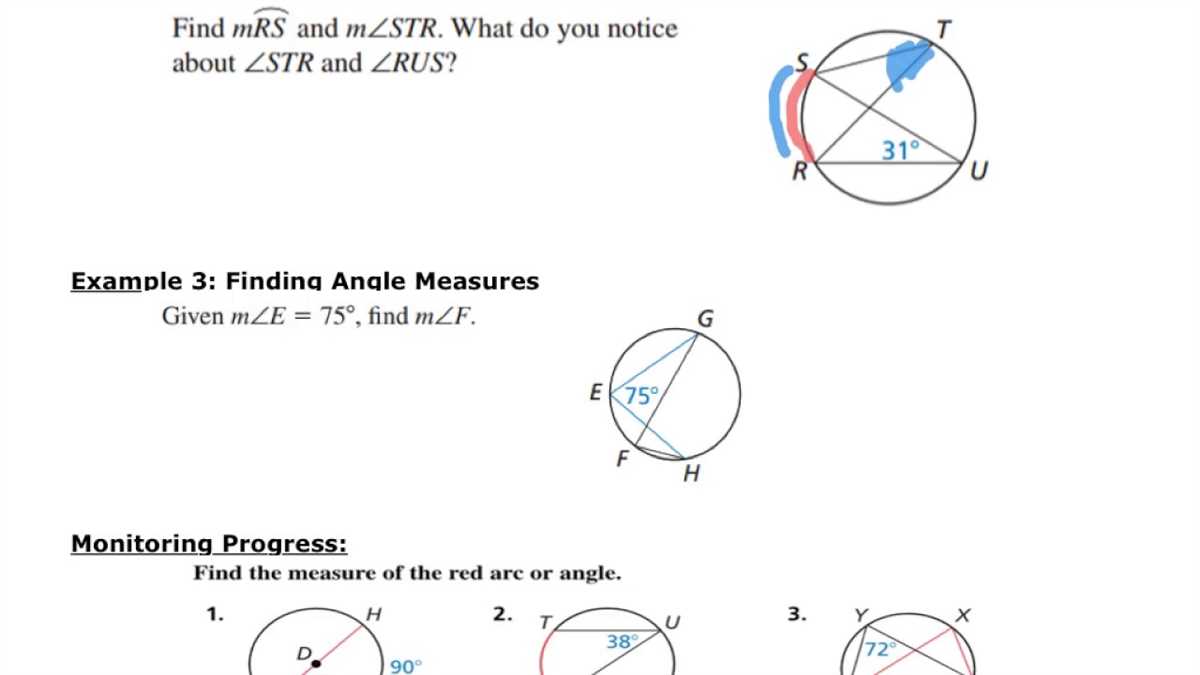
An inscribed angle is an angle formed by two chords in a circle with its vertex on the circle. To find the measure of an inscribed angle, we can use the properties and theorems related to arcs and angles in a circle.
Here are the steps to find the measure of an inscribed angle:
- Determine the intercepted arc: The intercepted arc is the arc that is formed by the sides of the inscribed angle. To find the measure of the intercepted arc, we can use the central angle theorem which states that the measure of a central angle is equal to the measure of its intercepted arc.
- Use the inscribed angle theorem: The inscribed angle theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. Therefore, once we determine the measure of the intercepted arc, we can simply divide it by 2 to find the measure of the inscribed angle.
- Apply any additional information: In some cases, additional information may be given such as the measure of another angle or the length of a segment. We can use this information along with the properties of inscribed angles to find the measure of the desired angle.
By following these steps and applying the appropriate theorems and properties, we can find the measure of an inscribed angle in a given circle. It is important to carefully analyze the given information and use the relevant formulas to ensure accurate results.
Solving practice problems involving inscribed angles
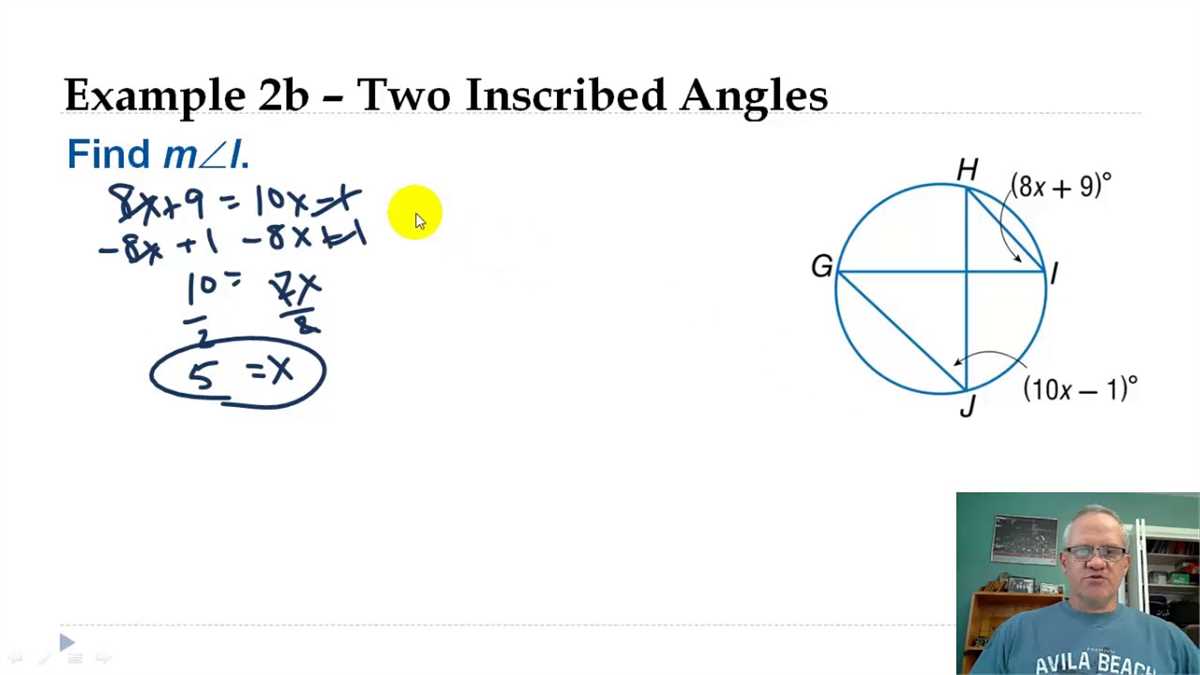
Inscribed angles are angles formed by two chords or a chord and a tangent that intersect on the circumference of a circle. These angles have some interesting properties that can be applied to solve various practice problems.
One of the key properties of inscribed angles is that the measure of an inscribed angle is equal to half the measure of its intercepted arc. This property can be used to find missing angles or arcs in a circle.
For example, if we are given an inscribed angle with a measure of 60 degrees and we are asked to find the measure of the intercepted arc, we can use the property that the measure of an inscribed angle is equal to half the measure of its intercepted arc. Therefore, the intercepted arc has a measure of 120 degrees.
In addition to the property mentioned above, there are also other properties of inscribed angles that can be used to solve practice problems. These properties include the angles formed by chords that intersect within the circle, angles formed by chords that intersect outside the circle, and angles formed by tangents and secants.
To solve practice problems involving inscribed angles, it is important to identify the relationships between the angles and arcs in the given scenario. By applying the properties of inscribed angles, we can determine the measures of missing angles or arcs and solve the practice problems successfully.
Properties of inscribed angles in different geometric shapes
In geometry, an inscribed angle is an angle whose vertex is on a circle and whose sides are chords of the circle. Inscribed angles have several interesting properties that can be observed in different geometric shapes.
In a triangle: When an angle of a triangle is inscribed in a circle, it is called an inscribed angle. The measure of an inscribed angle is always half the measure of its intercepted arc. This property can be used to find missing angles or arc lengths in a triangle.
In a quadrilateral: In a convex quadrilateral, the sum of the measures of the opposite inscribed angles is always 180 degrees. This property is known as the opposite angles theorem and can be used to determine the relationships between angles in a quadrilateral.
In a pentagon: In a regular pentagon, the measure of each interior angle is 108 degrees. If an inscribed angle in a regular pentagon intercepts a minor arc, its measure is half the measure of the intercepted arc. This property can be used to find the measure of unknown angles in a regular pentagon.
In a circle: In a circle, an inscribed angle and its intercepted arc are supplementary, meaning they add up to 180 degrees. This relationship can be applied to find the measure of unknown angles or arc lengths in a circle.
In summary: Inscribed angles have unique properties in different geometric shapes. Understanding these properties allows us to find missing angles, determine relationships between angles in a shape, and solve various geometry problems.
Summary and Key Takeaways about Inscribed Angles

Inscribed angles play an important role in geometry, specifically in the study of circles. These angles are formed by two chords, or by a chord and a tangent line, with the vertex of the angle lying on the circumference of the circle. Understanding the properties and relationships of inscribed angles can help solve various problems involving circles.
Here are some key takeaways about inscribed angles:
- Inscribed angles that intercept the same arc are congruent.
- An inscribed angle is half the measure of its intercepted arc.
- A central angle and its intercepted arc have the same measure.
- A diameter of a circle is the largest inscribed angle, measuring 180 degrees.
- Inscribed angles created by a chord and tangent line are congruent to half the measure of their intercepted arcs.
Understanding these concepts and properties can help solve problems that involve inscribed angles, such as finding missing angles in circle diagrams or proving congruence between different inscribed angles.
Overall, inscribed angles provide a useful tool for analyzing and solving problems related to circles. By recognizing their properties and relationships, mathematicians can make accurate conclusions and navigate the intricate world of circular geometry.