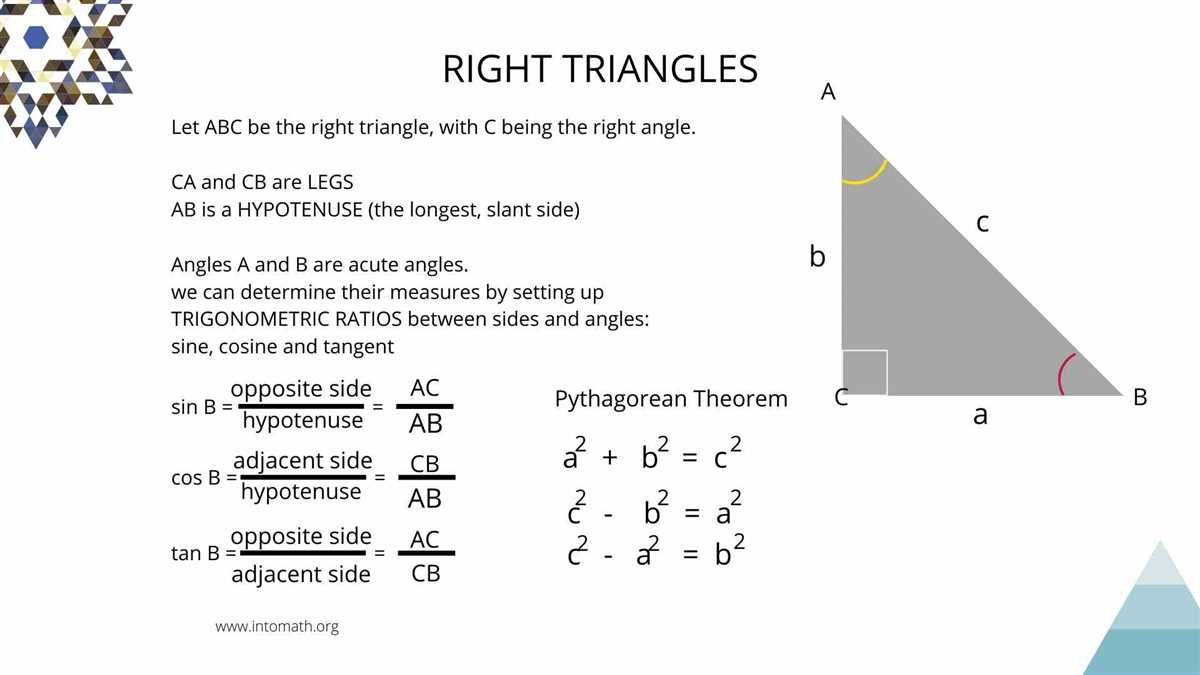
In Lesson 5.7 of your math class, you have learned about the Pythagorean Theorem. The Pythagorean Theorem is a crucial concept in geometry that helps us find the lengths of sides in a right triangle. This theorem is named after the ancient Greek mathematician, Pythagoras, who discovered it around 500 BC.
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In mathematical terms, if a and b are the lengths of the legs and c is the length of the hypotenuse, the theorem can be expressed as a^2 + b^2 = c^2.
During your practice problems in Lesson 5.7, you were given various right triangles and asked to find the length of a missing side using the Pythagorean Theorem. By applying the theorem and solving for the unknown variable, you were able to determine the length of the side, allowing you to fully define the triangle.
Understanding and applying the Pythagorean Theorem is essential in various fields, including architecture, engineering, and physics. This concept allows us to calculate distances, determine angles, and solve practical problems involving right triangles. By mastering the Pythagorean Theorem, you will have a valuable tool that can be applied across various mathematical disciplines.
Benefits of Lesson 5.7 Practice A: The Pythagorean Theorem Answer Key

The Pythagorean Theorem is a fundamental concept in geometry that states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. Lesson 5.7 Practice A provides an answer key to help students understand and apply this important theorem.
One of the benefits of having an answer key for Lesson 5.7 Practice A is that it allows students to check their work and verify their answers. This is crucial for self-assessment and ensures that students are on the right track. It also helps to build confidence and motivation, as students can see their progress and identify any areas where they may need additional practice.
Moreover, the answer key allows students to understand the process and logic behind solving problems using the Pythagorean Theorem. By comparing their solutions with the provided answers, students can learn from their mistakes and gain a deeper understanding of the concept. This promotes critical thinking and problem-solving skills.
In addition, the answer key can be used as a teaching tool by educators. They can review the answers with their students, discuss different approaches to solving the problems, and address any misconceptions. This promotes a collaborative learning environment where students can learn from each other’s strategies and perspectives.
Overall, Lesson 5.7 Practice A: The Pythagorean Theorem Answer Key is a valuable resource that helps students improve their understanding and application of the Pythagorean Theorem. It provides a means for self-assessment, promotes critical thinking, and fosters collaborative learning. By utilizing the answer key effectively, students can enhance their mathematical skills and confidence.
Enhancing Understanding of the Pythagorean Theorem

The Pythagorean theorem is a fundamental concept in geometry that relates to the relationship between the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. Understanding this theorem is crucial for solving problems involving right triangles and finding missing side lengths.
One way to enhance understanding of the Pythagorean theorem is through visualization. By using visual aids such as diagrams and interactive tools, students can better grasp the concept and see how the theorem applies to different right triangles. Visualizing the relationship between the sides of a triangle can help students develop a deeper understanding of the theorem and its applications.
To further solidify understanding, it is important for students to practice applying the Pythagorean theorem in various scenarios. By solving different types of problems and exercises, students can become more comfortable with the theorem and develop problem-solving skills. For example, they can calculate the length of a missing side in a right triangle, determine if a triangle is a right triangle based on its side lengths, or solve real-world problems involving distance and proportions.
Another effective approach to enhancing understanding is to connect the Pythagorean theorem to real-life situations. By relating the theorem to everyday examples, students can see the practical applications of the concept. For instance, they can explore how the theorem is used in architecture to ensure the stability of structures, or in navigation to calculate distances. Making these connections can make the theorem more meaningful and relatable.
Overall, enhancing understanding of the Pythagorean theorem involves visualizing the concept, practicing problem-solving, and connecting it to real-life situations. By employing these strategies, students can deepen their comprehension and apply the theorem to various mathematical and real-world problems.
Clarifying Concepts and Solving Problems
The Pythagorean Theorem is a fundamental concept in geometry that relates the lengths of the sides of a right triangle. It states that the sum of the squares of the lengths of the two shorter sides is equal to the square of the length of the longest side, which is called the hypotenuse. This theorem can be used to solve a variety of problems involving right triangles.
When using the Pythagorean Theorem to solve problems, it is important to understand the key concepts involved. First, it is essential to identify the right triangle in the problem and label its sides. The two shorter sides are typically referred to as the legs, while the longest side is called the hypotenuse. Next, we can use the Pythagorean Theorem equation (a^2 + b^2 = c^2) to find the unknown side length.
Let’s consider an example to clarify these concepts. Suppose we have a right triangle with one leg measuring 4 units and the hypotenuse measuring 5 units. To find the length of the other leg, we can plug in the known values into the Pythagorean Theorem equation: (4^2 + b^2 = 5^2). Solving for b, we get b^2 = 9, which means b = 3. Therefore, the length of the other leg is 3 units.
It is important to note that the Pythagorean Theorem can also be used to determine whether a triangle is a right triangle. If the sum of the squares of the lengths of the two shorter sides is equal to the square of the length of the longest side, then the triangle is a right triangle. If not, it is not a right triangle. This property can be helpful in problem-solving when we need to identify right triangles among a group of triangles.
In conclusion, understanding the concepts of the Pythagorean Theorem and how to apply it in problem-solving scenarios is crucial in geometry. By correctly identifying right triangles, labeling their sides, and using the Pythagorean Theorem equation, we can find unknown side lengths and determine if a triangle is a right triangle. This knowledge is valuable in various fields, such as architecture, engineering, and physics.
Boosting Confidence in Mathematics
Mathematics can be a challenging subject for many students. It requires logical thinking, problem-solving skills, and a solid understanding of mathematical concepts. However, with the right approach and support, it is possible to boost confidence in mathematics and excel in this subject.
1. Providing a supportive learning environment: Creating a positive and supportive learning environment is crucial for boosting confidence in mathematics. Teachers should encourage students to ask questions, participate in class discussions, and collaborate with their peers. It is important to create a safe space where students feel comfortable making mistakes and learning from them.
2. Breaking down complex concepts: Mathematics can often seem overwhelming due to its complexity. Breaking down complex concepts into smaller, more manageable parts can help students understand and grasp the material better. Teachers should use visual aids, real-life examples, and hands-on activities to make abstract concepts more concrete and relatable.
- 3. Building a strong foundation: A strong foundation in mathematics is essential for students to feel confident in tackling more advanced topics. Teachers should ensure that students have a solid understanding of basic mathematical concepts and skills before moving on to more complex topics. Regular revision and practice of foundational concepts can help reinforce understanding and build confidence.
- 4. Encouraging problem-solving skills: Problem-solving is a key aspect of mathematics. Encouraging students to think critically, analyze problems, and come up with creative solutions can boost their confidence in their mathematical abilities. Teachers should provide opportunities for students to solve challenging problems and guide them through the problem-solving process.
- 5. Celebrating achievements: Recognizing and celebrating students’ achievements in mathematics can significantly boost their confidence. Teachers should acknowledge and praise students’ efforts, progress, and improvements. This positive reinforcement can motivate students to continue working hard and believe in their abilities.
In conclusion, boosting confidence in mathematics requires a supportive learning environment, breaking down complex concepts, building a strong foundation, encouraging problem-solving skills, and celebrating achievements. By implementing these strategies, teachers can help students overcome their math anxiety and develop a positive attitude towards mathematics.
Improving Test Performance
A high-stakes test can make even the most prepared student feel anxious. However, there are strategies that can help improve test performance and alleviate test anxiety.
Time management: One key factor in test performance is effective time management. It is important to allocate enough time for each question or section of the test. Start by reviewing the test instructions and determining how much time can be spent on each question. This will help prevent rushing through questions and allow for proper thought and consideration.
Study techniques: Another important aspect of improving test performance is using effective study techniques. These may include creating flashcards, summarizing lecture notes, or practicing with sample questions. By actively engaging with the material, students can retain information more effectively and feel more confident during the test.
Organized notes: Keeping organized notes can also contribute to better test performance. When notes are well-organized, it is easier to review and understand the material. This can save time during studying and help prevent confusion during the test.
Test-taking strategies: Finally, using specific test-taking strategies can improve performance. This may include reading the questions carefully, identifying keywords, eliminating obviously incorrect answers, and budgeting time accordingly. Learning these strategies can help students approach tests with a clear and focused mindset.
Supplementing Classroom Learning
In today’s fast-paced world, classroom learning is no longer limited to the traditional methods of textbooks and lectures. As technology continues to advance, there are now various tools and resources available that can supplement and enhance classroom learning for students of all ages. These supplementary materials provide additional support and help students gain a deeper understanding of the subjects they are studying.
One popular way to supplement classroom learning is through online educational platforms. These platforms offer a wide range of courses and videos that cover various topics. Students can access these resources at any time and from any location, making learning more flexible and convenient. Online platforms also often provide interactive elements, such as quizzes and discussion forums, which can further engage students and encourage active participation.
Another effective way to supplement classroom learning is through hands-on activities and experiments. This allows students to apply the theories and concepts they have learned in a practical setting, which can greatly enhance their understanding and retention of the material. For example, in a science class, students can conduct experiments to observe the effects of different variables, fostering a deeper understanding of the scientific principles at play.
Additionally, field trips and guest speakers can provide valuable real-world experiences and insights that go beyond the scope of the classroom. Visiting museums, historical sites, or companies related to the subjects being studied can give students a firsthand look at how concepts are applied in the real world. Guest speakers from relevant industries can share their experiences and provide practical advice, giving students a glimpse into potential career paths.
- Visual aids, such as charts, diagrams, and graphs, are also highly effective in supplementing classroom learning. Visual representations can help students better understand complex concepts and visualize relationships between different variables. Teachers can use these aids in their lectures or assign them as projects for students to create and present their own visual materials.
- Collaborative learning is another powerful supplement to classroom learning. Working in groups or pairs allows students to exchange ideas, discuss topics, and solve problems together. This not only enhances their understanding of the material but also develops important teamwork and communication skills.
- Finally, practice exercises and self-assessment tools can help students reinforce what they have learned in the classroom. Interactive quizzes, worksheets, and online practice platforms allow students to test their knowledge and identify areas they need to work on. This self-paced learning approach can help students build confidence and take ownership of their education.
Overall, supplementing classroom learning with various tools and resources can greatly benefit students. It provides them with different perspectives, opportunities for hands-on learning, and access to additional support and materials. By combining traditional methods with these supplementary approaches, educators can create a more engaging and effective learning environment.
Facilitating Self-Study and Review
Self-study and review are essential components of effective learning. By engaging in these activities, students can reinforce their understanding of the material, identify areas where they need further practice, and build their confidence in applying the concepts learned.
To facilitate self-study and review, it is important to provide students with resources and tools that can support their independent learning. Here are some strategies that can be used:
- Online platforms: Utilize online platforms such as educational websites, learning management systems, and interactive applications that offer a variety of practice exercises, quizzes, and games. These platforms can provide students with immediate feedback, track their progress, and offer personalized recommendations for further practice.
- Study guides: Create or provide students with study guides that summarize the key concepts and provide examples and practice questions. These guides can serve as a reference during self-study sessions and help students focus on the most important information.
- Peer collaboration: Encourage students to form study groups or find a study buddy. Collaborating with peers allows students to discuss and explain concepts to one another, ask and answer questions, and gain a deeper understanding of the material.
- Scheduled review sessions: Set aside dedicated time for review sessions where students can ask questions and receive clarification on concepts they find challenging. These sessions can be conducted in person or virtually, depending on the circumstances.
Overall, a combination of these strategies can empower students to take ownership of their learning and develop the skills necessary for self-study and review. By providing the necessary resources, guidance, and support, educators can help students build their confidence, improve their academic performance, and become lifelong learners.