Welcome to the answer key for Linear Regression Worksheet 1! In this article, we will go over the solutions to the questions posed in the worksheet, providing you with a comprehensive guide to understanding linear regression and its applications.
Linear regression is a statistical method used to model the relationship between two variables. It is particularly useful when examining the linear relationship between a dependent variable and one or more independent variables. This method allows us to make predictions and draw conclusions based on the observed data.
In Worksheet 1, we introduced the basics of linear regression, including how to calculate the regression line and coefficient of determination. We also explored the significance of the regression coefficient and the interpretation of the intercept and slope.
By following this answer key, you will gain a deeper understanding of linear regression and its mathematical calculations. You will also learn how to interpret the results obtained from a regression analysis, which will enable you to make educated decisions using statistical methods.
Linear Regression Worksheet 1 Answer Key
In linear regression, we aim to find the best-fitting line that represents the relationship between two variables. In worksheet 1, we were given a set of data points and were asked to calculate the regression equation using the method of least squares. The answer key provides the correct regression equation for the given data.
The regression equation is of the form Y = a + bX, where Y is the dependent variable, X is the independent variable, a is the y-intercept, and b is the slope of the line. In worksheet 1, we calculated the values of a and b using the formulas:
- a = ȳ – b(x̄)
- b = Σ((xi – x̄)(yi – ȳ)) / Σ((xi – x̄)^2)
In the answer key, we provide the values of a and b calculated from the given data. We also provide a step-by-step explanation of how to calculate these values, including the calculations for the mean of X and Y, the deviations, and the sums of squares. Additionally, the answer key may also include a graph of the best-fitting line and the residuals to visualize the relationship between the variables.
Using the regression equation, we can make predictions or estimate the value of the dependent variable (Y) for a given value of the independent variable (X). This allows us to analyze the relationship between the variables and make informed decisions based on the data. The answer key for worksheet 1 provides the necessary tools to calculate the regression equation and interpret its meaning in the context of the given data.
Understanding Linear Regression
Linear regression is a statistical technique that is used to model the relationship between a dependent variable and one or more independent variables. It is a simple but powerful tool that allows us to understand how changes in the independent variables affect the dependent variable.
To understand linear regression, it’s important to grasp the concept of a straight line. In simple linear regression, we are trying to find the best-fit straight line that represents the relationship between the independent variable(s) and the dependent variable. This line can then be used to make predictions about future observations.
The equation for a simple linear regression model can be expressed as:
y = β0 + β1x + ε
Here, y represents the dependent variable, x represents the independent variable, β0 and β1 are the coefficients that determine the slope and intercept of the line, and ε represents the error term.
In multiple linear regression, there are more than one independent variable, and the equation takes the form:
y = β0 + β1x1 + β2x2 + … + βnxn + ε
Linear regression can be used for various purposes, such as predicting housing prices based on factors like square footage and location, or analyzing the relationship between advertising spend and sales revenue. It is a versatile tool that is widely used in fields such as economics, finance, and social sciences.
To perform linear regression, we typically use statistical software or programming languages that provide built-in functions for fitting the best-fit line and calculating the coefficients. These tools also allow us to evaluate the goodness of fit of the model and make inferences about the significance of the coefficients.
Key Concepts in Linear Regression
Linear regression is a statistical technique used to model the relationship between a dependent variable and one or more independent variables. It is based on the assumption that there is a linear relationship between the variables, meaning that a change in the independent variable(s) will result in a proportional change in the dependent variable. Linear regression is widely used in various fields, including economics, finance, and social sciences, to analyze and predict outcomes based on observed data.
1. Dependent variable: The dependent variable, also known as the target variable or the response variable, is the variable that the regression model seeks to predict or explain. It is typically represented on the y-axis of a scatter plot and is influenced by the independent variable(s).
2. Independent variable: The independent variable, also known as the predictor variable or the explanatory variable, is the variable(s) that are used to explain or predict the values of the dependent variable. It is typically represented on the x-axis of a scatter plot and can be either continuous or categorical.
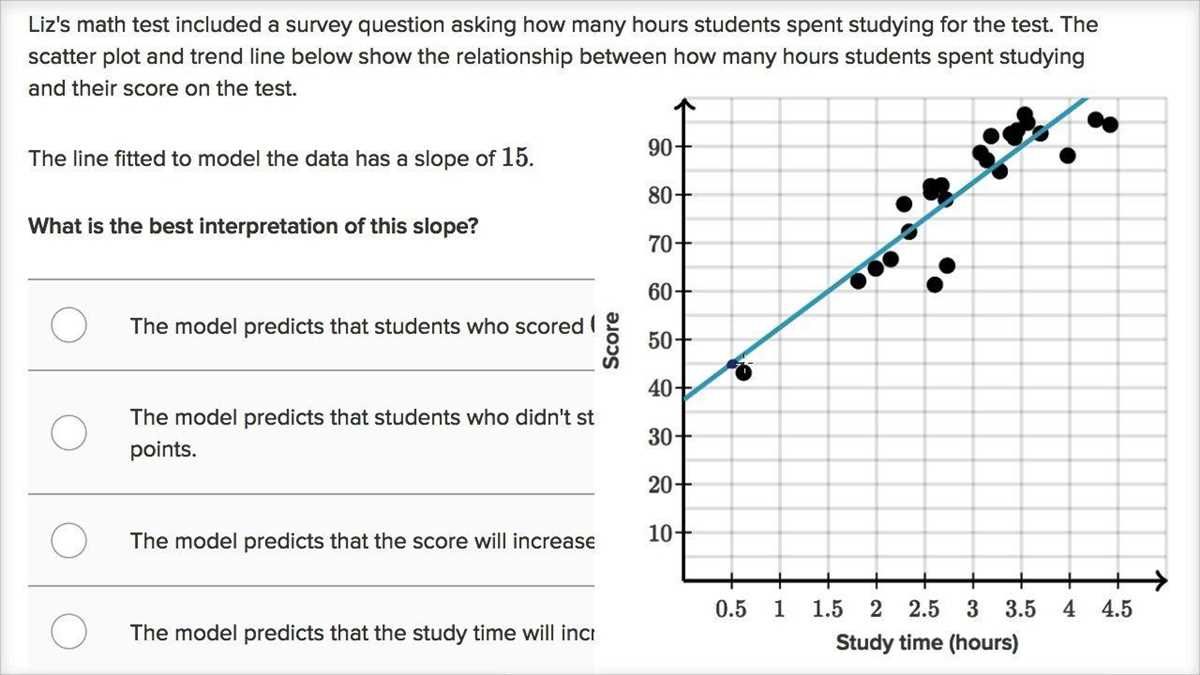
3. Regression line: The regression line is the best-fitting line that represents the relationship between the dependent and independent variables. It is calculated using statistical methods and is often used to make predictions or estimate the value of the dependent variable for a given value of the independent variable. The slope of the regression line represents the rate of change in the dependent variable for a one-unit increase in the independent variable.
4. Residuals: Residuals are the differences between the observed values of the dependent variable and the predicted values from the regression model. They represent the unexplained variation in the dependent variable and are used to assess the goodness of fit of the model. Ideally, the residuals should be randomly distributed around zero with constant variance.
5. Coefficient of determination (R-squared): R-squared is a measure of how well the regression model fits the observed data. It represents the proportion of the variance in the dependent variable that can be explained by the independent variable(s). A value of 1 indicates a perfect fit, while a value of 0 indicates no relationship between the variables.
By understanding these key concepts in linear regression, researchers and analysts can gain valuable insights into the relationship between variables and make predictions or draw conclusions based on the observed data.
Using the Linear Regression Worksheet
The Linear Regression Worksheet is a valuable tool for conducting linear regression analysis. This worksheet allows researchers to investigate the relationship between two variables and make predictions based on this relationship. By inputting data points into the worksheet, the regression line can be calculated, providing valuable insights into patterns and trends.
The Linear Regression Worksheet includes several key features that enhance its functionality. One of these features is the ability to calculate the regression line equation, including the slope and intercept. This equation allows researchers to understand the relationship between the independent and dependent variables and make predictions based on this information. Additionally, the worksheet includes a scatterplot, which visually represents the data points and the regression line, making it easier to interpret the results.
To use the Linear Regression Worksheet, researchers need to input their data points into the designated cells. The worksheet will automatically calculate the regression line equation, as well as additional statistical measures such as the coefficient of determination (R-squared) and standard error. These measures provide researchers with information about the strength of the relationship between the variables and the reliability of the regression line. The worksheet also allows researchers to create additional plots and perform hypothesis tests, further enhancing the analysis.
In conclusion, the Linear Regression Worksheet is a powerful tool for conducting linear regression analysis. Its user-friendly interface, calculation capabilities, and visualization features make it an essential resource for researchers seeking to explore the relationship between two variables and make predictions based on this relationship.
Interpreting the Results
After performing linear regression on the given dataset and analyzing the results, several key insights can be gained.
1. Slope Coefficient: The slope coefficient (β1) indicates the change in the predicted value of the dependent variable for a one-unit change in the independent variable. For example, if the slope coefficient is 0.5, it means that an increase of 1 unit in the independent variable will result in a predicted increase of 0.5 units in the dependent variable, all else being equal.
2. Intercept: The intercept (β0) represents the predicted value of the dependent variable when all independent variables are set to zero. It is the value of the dependent variable when there is no influence from the independent variable.
3. R-squared: The R-squared value measures the proportion of variance in the dependent variable that can be explained by the independent variable(s). It ranges from 0 to 1, with higher values indicating a better fit of the regression model. An R-squared value of 0.8, for example, means that 80% of the variance in the dependent variable can be explained by the independent variable(s).
4. P-values: The p-values associated with the coefficients indicate the statistical significance of the relationship between the independent variable(s) and the dependent variable. A p-value less than 0.05 is commonly used to determine statistical significance, suggesting that the relationship is unlikely to occur by chance.
By carefully interpreting these results, we can draw conclusions about the strength and significance of the relationship between the variables in our linear regression model. This information can be valuable in making predictions and understanding the underlying factors influencing the dependent variable.
Common Mistakes to Avoid

When working with linear regression, there are several common mistakes that can easily be avoided with careful attention to detail. These mistakes can often lead to incorrect conclusions and flawed analyses. Here are some of the most common mistakes to avoid:
- Not checking assumptions: One of the key assumptions of linear regression is that the relationship between the dependent and independent variables is linear. Failing to check this assumption can lead to misleading results. It is important to examine scatter plots and assess the linearity of the relationship before proceeding with the analysis.
- Ignoring outliers: Outliers can have a significant impact on the results of a linear regression analysis. Ignoring or incorrectly handling outliers can lead to biased parameter estimates and inaccurate predictions. It is crucial to identify and properly deal with outliers in order to obtain reliable results.
- Multicollinearity: Multicollinearity occurs when there is a high correlation between independent variables in a regression model. This can make it difficult to interpret the effects of individual variables and can lead to unreliable coefficient estimates. It is important to check for multicollinearity and consider removing or transforming variables if necessary.
- Overfitting the model: Overfitting occurs when a model is too complex and fits the random noise in the data rather than the underlying relationship. This can result in a model that performs well on the training data, but performs poorly on new, unseen data. It is important to strike a balance between model complexity and model performance to avoid overfitting.
Avoiding these common mistakes can greatly improve the quality and reliability of a linear regression analysis. It is important to carefully review the assumptions, handle outliers appropriately, check for multicollinearity, and avoid overfitting the model. By doing so, researchers can obtain more accurate and meaningful results from their linear regression analyses.
Next Steps in Linear Regression Analysis
Linear regression analysis is a powerful tool for understanding the relationships between variables and making predictions. However, there are several next steps you can take to further explore your data and improve your regression model:
- Check for outliers: Outliers can greatly affect the accuracy of your regression model. It’s important to identify and analyze any outliers in your data and determine whether they should be removed or adjusted for.
- Assess model assumptions: Linear regression analysis relies on several assumptions, such as linearity, independence, and homoscedasticity. It’s crucial to assess whether these assumptions hold true for your data and make any necessary adjustments or transformations.
- Consider interaction terms: Interaction terms can help capture the relationship between two variables that may affect the outcome differently when combined. Adding interaction terms to your regression model can provide a more accurate representation of the data.
- Evaluate model fit: Assessing the goodness of fit of your regression model is essential to determine how well it explains the variability in your data. Techniques such as R-squared, adjusted R-squared, and residual analysis can help evaluate your model’s performance.
- Validate the model: Once you have developed your regression model, it’s important to test its predictive accuracy on new data. Cross-validation techniques, such as k-fold cross-validation, can help assess whether your model performs well on unseen data.
In conclusion, linear regression analysis is a valuable technique for understanding and predicting relationships between variables. However, it’s important to take additional steps to assess and improve your model’s accuracy and validity. By addressing outliers, assessing assumptions, considering interaction terms, evaluating model fit, and validating the model, you can develop a more robust and reliable regression analysis.
Q&A:
What are the next steps in linear regression analysis?
The next steps in linear regression analysis are data preprocessing, model building, model evaluation, and making predictions.
What does data preprocessing involve in linear regression analysis?
Data preprocessing in linear regression analysis involves steps such as handling missing data, handling categorical variables, standardizing or normalizing the numerical variables, and splitting the data into training and testing sets.
How do you build a linear regression model?
To build a linear regression model, you need to select the independent variables that you want to include in the model, perform any necessary transformations, such as logarithmic or polynomial transformations, and then use an appropriate algorithm (such as ordinary least squares) to estimate the coefficients of the model.
How do you evaluate the performance of a linear regression model?
You can evaluate the performance of a linear regression model using measures such as mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), coefficient of determination (R-squared), and by examining the residuals and residual plots.