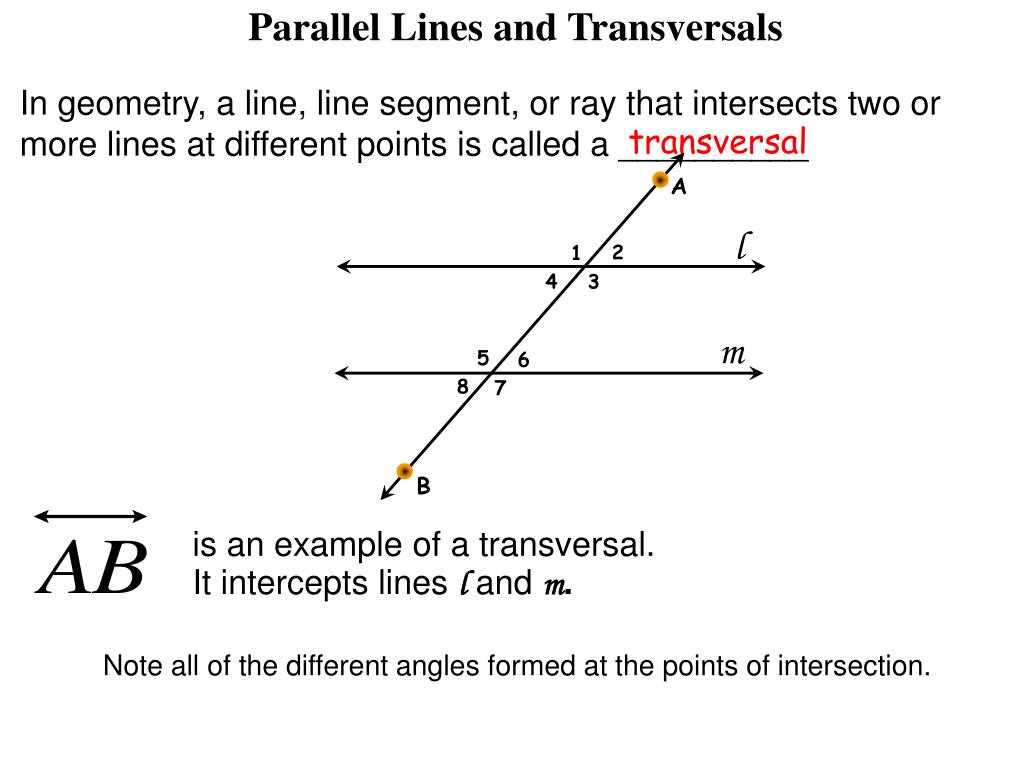
If you’re learning about parallel lines, transversals, and angles, then you’ve probably come across the parallel lines cut by a transversal coloring activity. This activity is a fun and engaging way to practice identifying and classifying angles formed by parallel lines and a transversal.
To successfully complete this activity, it’s important to understand the properties of parallel lines and the corresponding angle relationships. When a line intersects two parallel lines, it creates eight angles. These angles can be classified as corresponding angles, alternate interior angles, alternate exterior angles, or consecutive interior angles.
With the parallel lines cut by a transversal coloring activity, you are given a diagram with multiple angles formed by parallel lines and a transversal. Your task is to identify the type of angle and color it according to the key provided. This helps reinforce your understanding of the different angle relationships and how they are related to the position of the parallel lines and the transversal.
Understanding Parallel Lines and Transversals
In geometry, parallel lines are lines in a plane that never intersect. They are always the same distance apart. A transversal is a line that intersects two or more other lines. When a transversal intersects two parallel lines, it creates several angles with specific properties.
One property of parallel lines and transversals is that corresponding angles are congruent. Corresponding angles are the paired angles formed by a transversal and two parallel lines on opposite sides of the transversal. For example, if two parallel lines are cut by a transversal, angle 1 and angle 5 are corresponding angles and they are congruent.
Another property is that alternate interior angles are congruent. Alternate interior angles are the angles between two lines and on opposite sides of the transversal. For instance, if two parallel lines are cut by a transversal, angle 4 and angle 5 are alternate interior angles and they are congruent.
Understanding parallel lines and transversals is essential in geometry as it allows for the identification and analysis of various angle relationships. By recognizing these properties, students can confidently solve problems involving parallel lines and transversals, such as finding missing angle measures or proving geometric theorems.
The Concept of Parallel Lines and Transversals

Parallel lines and transversals are fundamental concepts in geometry. When two lines are parallel, they will never intersect, no matter how far they are extended. On the other hand, a transversal is a line that intersects two or more other lines. Understanding the properties and relationships between parallel lines and transversals is crucial in solving various geometric problems and proofs.
One key property of parallel lines is that they have the same slope. If two lines have the same slope, they will never intersect and are considered parallel. Another property is that parallel lines have corresponding angles that are congruent. These corresponding angles are formed when a transversal intersects the parallel lines. Identifying and applying these properties allows us to make accurate deductions and calculations when working with parallel lines and transversals.
Parallel lines and transversals also play a significant role in various real-world applications. For example, in architecture and construction, parallel lines are used to create symmetrical designs and ensure structural stability. In transportation, road markings and lanes are often designed using parallel lines and transversals to guide and organize traffic. Furthermore, parallel lines and transversals are used in computer graphics and animation to create realistic three-dimensional objects and scenes.
Overall, understanding the concept of parallel lines and transversals is essential in geometry and has wide-ranging applications in various fields. By studying and applying the properties and relationships associated with parallel lines and transversals, we can analyze and solve geometric problems with precision and accuracy. Whether it’s in mathematics, engineering, or even everyday life, the concepts of parallel lines and transversals are invaluable tools for understanding and manipulating our physical world.
Properties of Parallel Lines and Transversals

When two lines are parallel, they will never intersect. This important property allows us to make certain conclusions about the relationships between angles formed by parallel lines and transversals. When a transversal crosses parallel lines, it creates eight different angles. These angles can be classified as corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles.
Corresponding angles: These are angles that are in the same position relative to the transversal and the parallel lines. Corresponding angles are congruent, meaning they have the same measure.
Alternate interior angles: These are angles that are on opposite sides of the transversal and inside the parallel lines. Alternate interior angles are congruent.
Alternate exterior angles: These are angles that are on opposite sides of the transversal and outside the parallel lines. Alternate exterior angles are congruent.
Consecutive interior angles: These are angles that are on the same side of the transversal and between the parallel lines. Consecutive interior angles are supplementary, meaning their measures add up to 180 degrees.
Understanding the properties and relationships between angles formed by parallel lines and transversals is crucial in geometry and can help solve various problems involving angles and parallel lines.
Exploring the Relationships Between Angles
When we are exploring the relationships between angles, it is important to understand the different types of angles that can be formed when parallel lines are cut by a transversal. One type of angle is the vertical angle, which are formed when two lines intersect. Vertical angles are congruent, meaning they have the same measure.
Another type of angle that can be formed is the corresponding angle. Corresponding angles are on the same side of the transversal but on different lines. They are congruent if the lines are parallel. These angles can be used to determine whether or not two lines are parallel.
There are also alternate interior angles and alternate exterior angles. Alternate interior angles are on opposite sides of the transversal and inside the two lines. They are congruent if the lines are parallel. Similarly, alternate exterior angles are on opposite sides of the transversal and outside the two lines. They are also congruent if the lines are parallel.
By identifying these different types of angles and exploring their relationships, we can make deductions about the properties of lines and angles. This knowledge is valuable in geometry and can be applied to solve various problems involving parallel lines and transversals.
Overall, exploring the relationships between angles in the context of parallel lines and transversals is an essential concept in geometry. It allows us to identify congruent angles and determine parallelism between lines. Understanding these relationships enables us to solve problems involving angles and lines more effectively.
Coloring Activity: Parallel Lines and Transversals

In this coloring activity, students will explore the relationship between parallel lines and transversals. By identifying and coloring different angles formed by the intersection of parallel lines and a transversal, students will deepen their understanding of angle relationships and their properties.
First, students will be provided with a worksheet that contains a pair of parallel lines intersected by a transversal. Using different colors, students will color different angles based on their properties. For example, they might color all corresponding angles blue, all alternate interior angles green, and all same-side interior angles yellow. This color-coding system helps students visually distinguish between different angle relationships.
The activity not only engages students in hands-on learning but also encourages critical thinking. By analyzing the angles and their relationships, students can make conjectures and discover patterns. They can observe that corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary.
Furthermore, this coloring activity can be extended to include more complex angle relationships, such as vertical angles and angle sums on a straight line. Students can continue to color-code and explore these additional relationships, reinforcing their understanding of angles and parallel lines.
By participating in this coloring activity, students can develop their spatial reasoning skills, strengthen their knowledge of angle relationships, and deepen their understanding of parallel lines and transversals. It provides an interactive and engaging way for students to explore and internalize key concepts in geometry.
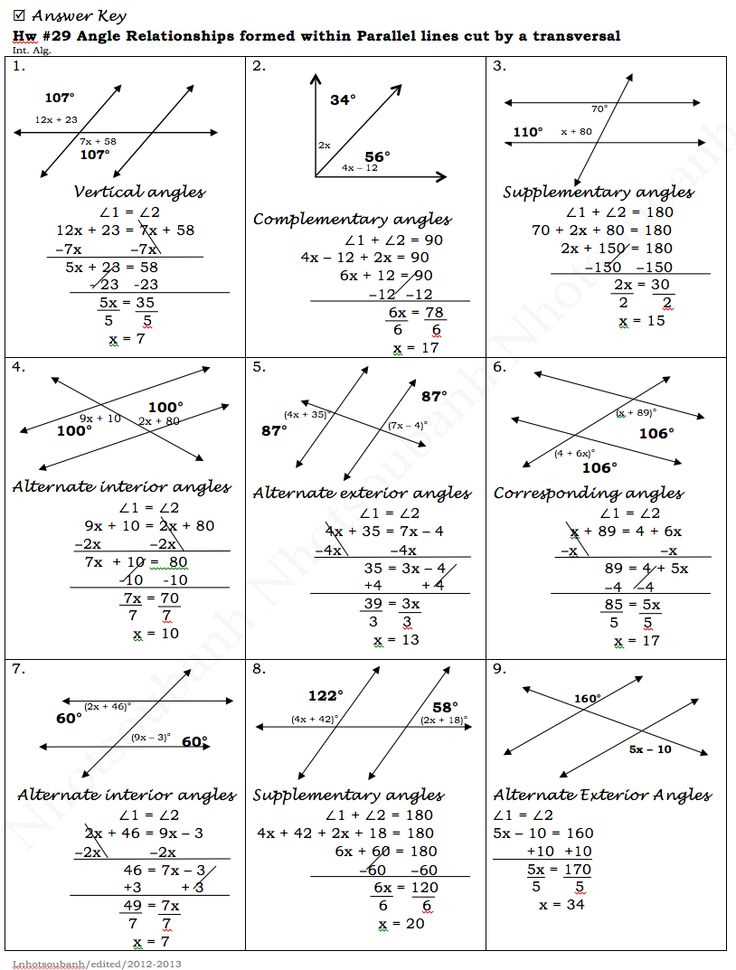
Answers to the Coloring Activity
In this coloring activity, students were asked to color various angles formed by parallel lines cut by a transversal. Here are the answers to the different angles:
Corresponding Angles:

- Angle 1 – Red
- Angle 2 – Blue
- Angle 3 – Green
- Angle 4 – Yellow
Alternate Interior Angles:
- Angle 5 – Pink
- Angle 6 – Orange
Alternate Exterior Angles:
- Angle 7 – Purple
- Angle 8 – Brown
Consecutive Interior Angles:
- Angle 9 – Gray
- Angle 10 – Light Blue
The use of different colors helps students visually differentiate between the different types of angles formed by parallel lines and a transversal. By coloring the angles correctly, students can better understand and remember the relationships between these types of angles.
This activity not only reinforces the concepts of parallel lines and transversals, but also allows students to engage in a hands-on and visual learning experience. By actively participating in the coloring activity, students can actively explore and internalize the properties and relationships of the angles formed by parallel lines and a transversal.