Understanding parent functions and transformations is a fundamental concept in mathematics. A parent function is the simplest form of a function that represents a particular family of functions. It serves as a template or blueprint for other functions within that family. Transformations, on the other hand, modify the graph of a parent function with shifts, stretches, compressions, and reflections.
A worksheet on parent functions and transformations is a valuable tool for practicing and reinforcing these concepts. It provides a set of problems that require students to identify the parent function, describe the transformation(s) applied to it, and graph the resulting function. The worksheet usually includes multiple-choice questions, fill-in-the-blank questions, and graphing exercises.
The answers to the parent functions and transformations worksheet in PDF format serve as a guide for students to check their work and gauge their understanding of the material. They can compare their answers with the correct solutions to identify any mistakes or areas for improvement. The answers may include the equation of the parent function, the equation of the transformed function, descriptions of the transformations, and the corresponding graphs.
Understanding Parent Functions and Transformations
The concept of parent functions and transformations is key to understanding how graphs can be modified and shifted. Parent functions serve as a baseline or template to which transformations can be applied. By understanding the characteristics of parent functions, we can better comprehend how these functions are altered through different transformations.
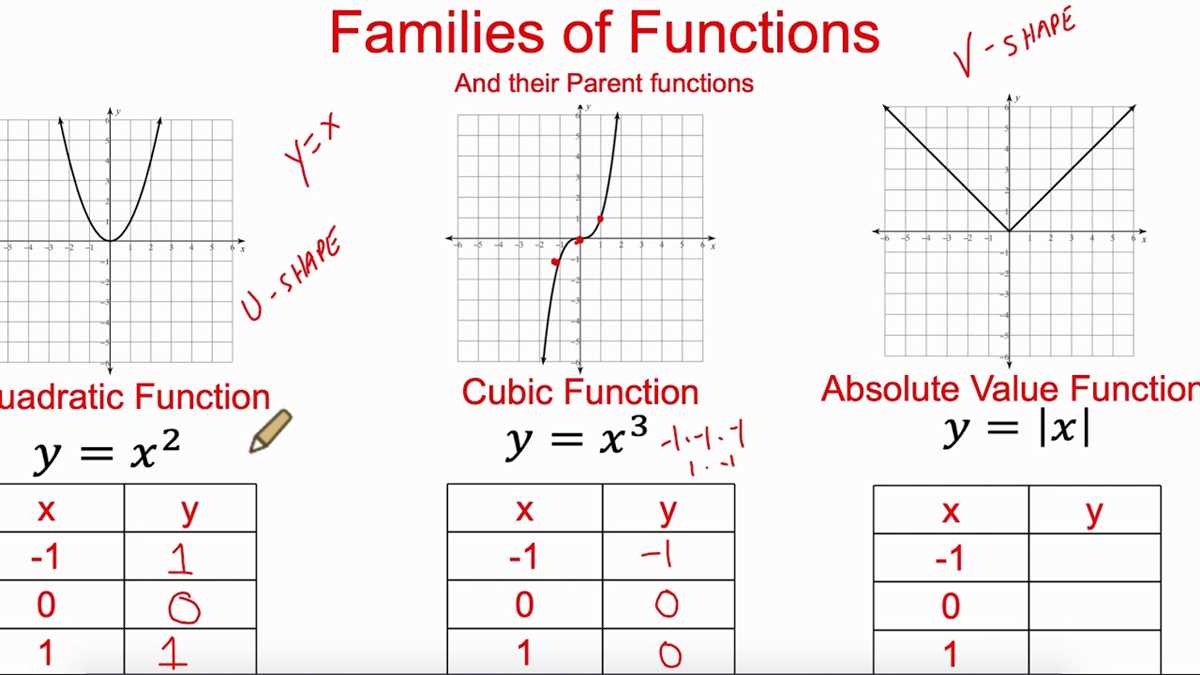
A parent function is a fundamental function that represents a particular family of functions. Examples of common parent functions include linear, quadratic, exponential, and trigonometric functions. These parent functions have distinct shapes and characteristics that can be modified using transformations.
In mathematics, transformations are changes made to the basic form of a parent function. There are four primary types of transformations: translations, reflections, stretches/compressions, and vertical shifts. Translations involve shifting the graph horizontally or vertically, reflections flip the graph across an axis, stretches/compressions change the steepness or width of the graph, and vertical shifts move the graph up or down.
Understanding how parent functions and transformations relate to each other allows us to analyze and interpret graphs more effectively. We can determine the effects of different transformations on a graph and accurately describe and predict their behavior. By studying parent functions and their transformations, we gain a deeper understanding of the principles and patterns underlying mathematical functions.
Section 2: Types of Parent Functions
In mathematics, parent functions serve as the foundation for various types of functions. They are simple functions that can be transformed and modified to create more complex functions. Understanding the different types of parent functions is crucial for studying mathematical transformations.
There are several common types of parent functions, each with its own distinctive characteristics and properties. These include:
- Linear Function: The linear function, represented by the equation y = mx + b, is a basic straight line that has a constant rate of change. It is one of the simplest and most commonly used parent functions.
- Quadratic Function: The quadratic function, represented by the equation y = ax^2 + bx + c, forms a parabola. It has a specific curvature and can open upwards or downwards depending on the coefficient a.
- Absolute Value Function: The absolute value function, represented by the equation y = |x|, graphs a V-shaped curve. It reflects any negative values of x to their positive counterparts and results in a symmetric graph.
- Square Root Function: The square root function, represented by the equation y = √x, returns the positive square root of a given value of x. Its graph starts at the origin and increases gradually as x increases.
- Exponential Function: The exponential function, represented by the equation y = a^x, involves exponential growth or decay. The graph of this function is typically a curve that rapidly increases or decreases depending on the value of the base a.
- Logarithmic Function: The logarithmic function, represented by the equation y = logₐx, is the inverse of an exponential function. It calculates the exponent to which a base a must be raised to obtain a certain value of x. The graph of this function is a curve that grows slowly as x increases.
These parent functions provide a basis for understanding more complex functions and their transformations. By studying their properties and behavior, mathematicians can further explore the interconnectedness of various mathematical concepts and applications.
Section 3: Characteristics of Parent Functions
In this section, we will explore the characteristics of parent functions, which are the basic functions that form the foundation for transformations. Understanding these characteristics is essential in order to effectively manipulate and graph functions.
1. Domain and Range:
The domain of a parent function is the set of all possible input values for the function. It represents the values that the independent variable can take. The range, on the other hand, is the set of all possible output values, representing the dependent variable. These sets can be identified by analyzing the behavior of the function as the input values approach positive and negative infinity.
2. Symmetry:
Symmetry is an important characteristic of parent functions. A function can be symmetric with respect to the y-axis (even symmetry), the x-axis (odd symmetry), or the origin (both even and odd symmetry). Understanding the symmetry of a parent function can help determine the symmetry of its transformed graph.
3. Intercept:
The intercepts of a parent function are the points where the graph intersects the x-axis (x-intercept) and the y-axis (y-intercept). These points can be found by setting the corresponding variable equal to zero and solving for the other variable. Intercepts provide valuable information about the function and can be used to graph the function.
4. Increasing and Decreasing:

A parent function can be either increasing or decreasing. If the function is increasing, the values of the dependent variable increase as the values of the independent variable increase. Conversely, if the function is decreasing, the values of the dependent variable decrease as the values of the independent variable increase. This information can be useful in graphing the function and determining the behavior of its transformations.
5. Vertical and Horizontal Asymptotes:
Vertical and horizontal asymptotes are lines that a graph approaches but never intersect. A parent function can have one or more vertical and horizontal asymptotes. The vertical asymptotes represent values where the function approaches infinity or negative infinity as the input values approach certain values. Horizontal asymptotes, on the other hand, represent values where the function approaches a specific horizontal value as the input values approach positive or negative infinity.
By understanding these characteristics of parent functions, we can better comprehend their behavior and use them as a foundation for transforming functions in more complex ways.
Section 4: Basics of Function Transformations
In this section, we will explore the basics of function transformations and how they can affect the shape, position, and behavior of parent functions. Understanding function transformations is essential for understanding more complex mathematical concepts and for solving real-world problems.
What are function transformations?
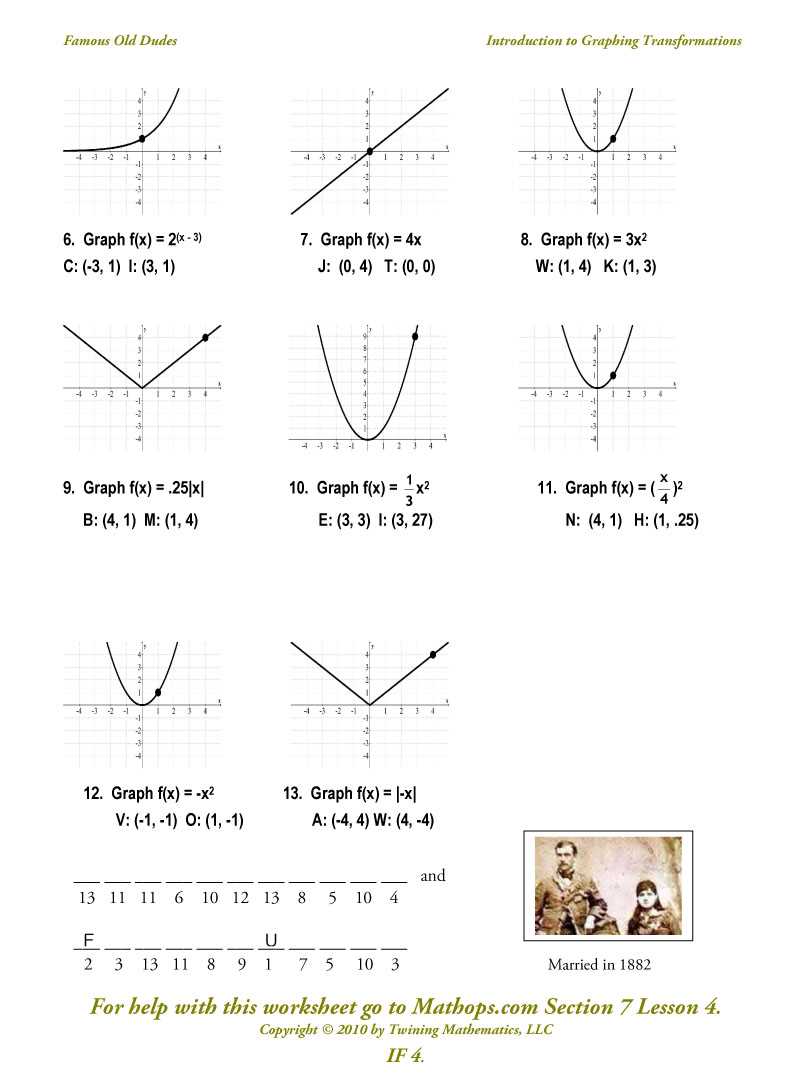
Function transformations are changes made to a parent function that alter its graph. These changes can include shifting the function horizontally or vertically, stretching or compressing the graph, reflecting it over an axis, or even combining multiple transformations.
Horizontal and vertical shifts
A horizontal shift moves the entire graph of the function left or right along the x-axis, while a vertical shift moves the graph up or down along the y-axis. These shifts are determined by adding or subtracting values inside the function equation.
Stretching and compressing
Stretching or compressing a function can change its slope, steepness, or overall shape. This is done by multiplying or dividing the values inside the function equation.
Reflections
A reflection over the x-axis or y-axis is a transformation that flips the graph of the function either vertically or horizontally. This is achieved by multiplying the function equation by -1.
Combining transformations
Multiple transformations can be combined to create more complex changes to a parent function. It is important to perform the transformations in a specific order to achieve the desired result.
Practical applications
Understanding function transformations is not only important in mathematics, but also in real-world situations. For example, in physics, function transformations can be used to model the behavior of objects in motion, such as the trajectory of a projectile.
In conclusion, function transformations allow us to manipulate and customize parent functions to fit specific needs. They are essential tools in mathematics and have practical applications in various fields.
Section 5: Applying Transformations to Parent Functions
In this section, we will explore how to apply transformations to parent functions. Transformations allow us to manipulate the shape, position, and size of a parent function to create new functions. Understanding how to apply these transformations is crucial in graphing functions and analyzing their properties.
There are four main transformations that can be applied to parent functions: translations, reflections, stretches, and compressions. Translations shift the graph horizontally or vertically, while reflections flip the graph across an axis. Stretches and compressions change the width or height of the graph.
To apply a translation, we add or subtract values to the x and/or y coordinates of the parent function. For example, adding a constant value to the x coordinates will shift the graph horizontally, while adding a constant value to the y coordinates will shift the graph vertically.
Reflections are applied by changing the sign of either the x or y coordinates. If the sign of the x coordinates is changed, the graph is reflected across the y-axis. If the sign of the y coordinates is changed, the graph is reflected across the x-axis.
Stretches and compressions are applied by multiplying the x and/or y coordinates by a constant value. A value greater than 1 will stretch the graph, while a value between 0 and 1 will compress it. Stretching or compressing along the x-axis will change the width of the graph, while stretching or compressing along the y-axis will change the height.
By combining these transformations, we can create a wide range of functions with different shapes and positions. It is important to practice applying these transformations to become proficient in graphing and analyzing functions.
Section 6: Worksheet with Answers for Practice
In this section, we provide a worksheet with answers for practice on parent functions and transformations. It is important to get hands-on practice to solidify your understanding of the concepts we have discussed so far.
Worksheet:
- Graph the parent function f(x) = x.
- Apply the transformation f(x) + 3 to the parent function and graph the result.
- Apply the transformation f(x – 2) to the parent function and graph the result.
- Apply the transformation 2f(x) to the parent function and graph the result.
- Apply the transformation -f(x) to the parent function and graph the result.
- Apply the transformation f(-x) to the parent function and graph the result.
Answers:
| Task | Graph |
|---|---|
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| 6 |  |
By practicing these transformations on the parent function, you will gain a better understanding of how they affect the shape, position, and orientation of a graph. Remember to carefully analyze the changes made by each transformation, and compare them to the original parent function.
With enough practice, you will become proficient in graphing and analyzing functions with various transformations. This knowledge will be invaluable when studying more complex functions and their applications.