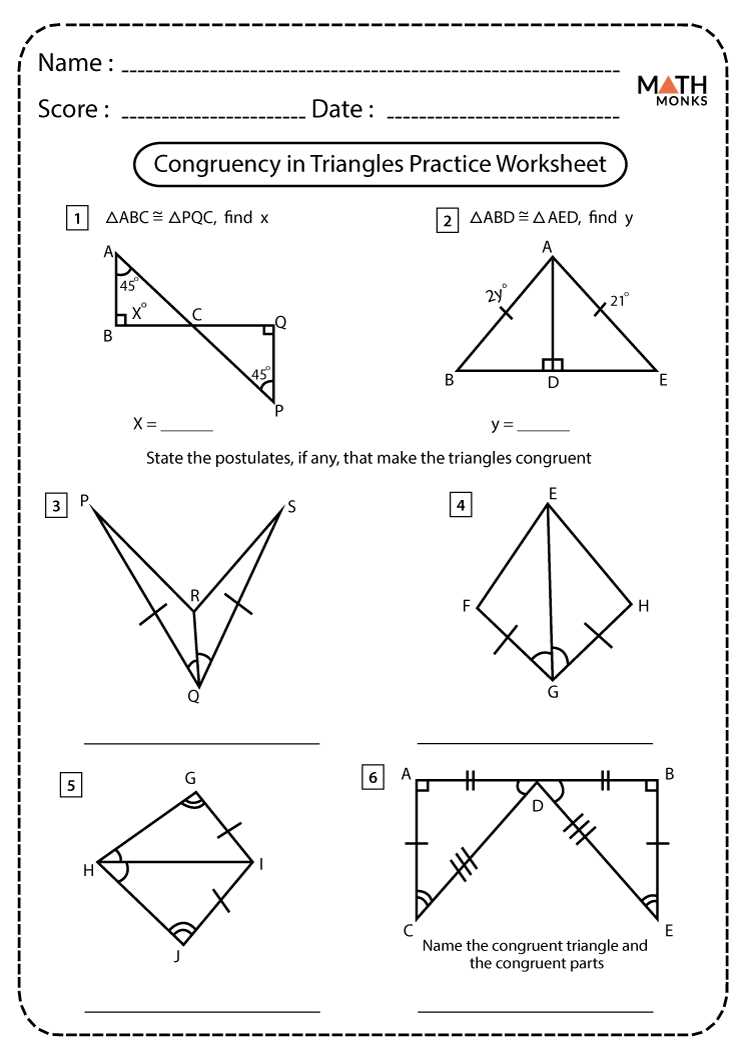
Similar triangles are a fundamental concept in geometry, and understanding their properties is crucial for solving various mathematical problems. When working with similar triangles, it is essential to identify and determine the relationships between their corresponding parts. One way to practice these skills is through a parts of similar triangles worksheet.
A parts of similar triangles worksheet typically consists of a series of questions and exercises that require students to find the missing sides and angles of similar triangles. These worksheets provide valuable practice in applying the principles of similarity and proportionality to solve geometric problems. They help students develop their problem-solving skills and reinforce their understanding of similar triangles.
Answering a parts of similar triangles worksheet requires knowledge of the properties of similar triangles, such as the fact that corresponding angles are congruent, and corresponding sides are in proportion. Students must identify corresponding parts, set up and solve proportions, and use geometric reasoning to deduce the missing values.
Understanding Similar Triangles
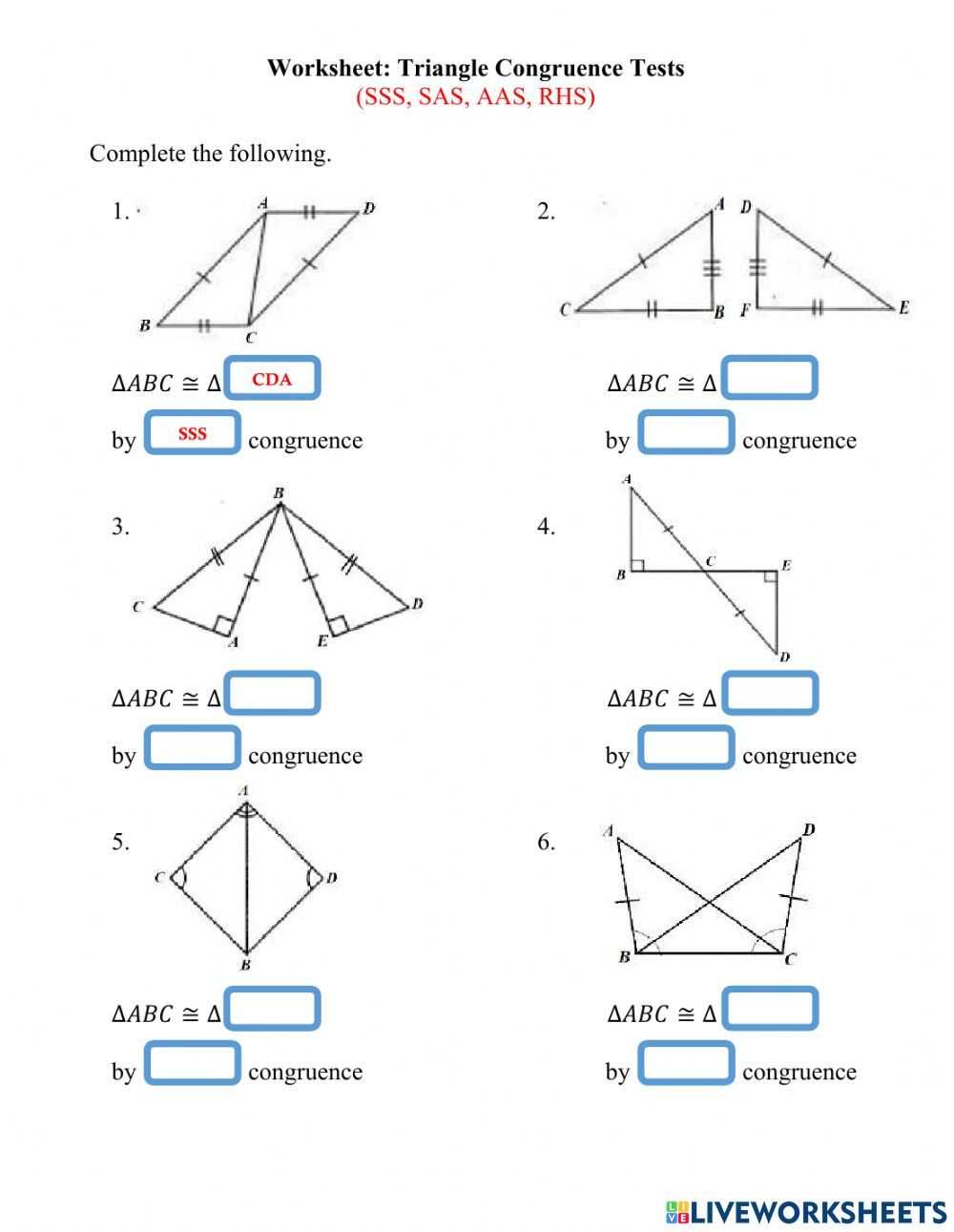
Similar triangles are a fundamental concept in geometry that involve two triangles with corresponding angles that are congruent and corresponding sides that are proportional. This means that if two triangles are similar, their corresponding angles will have the same measurement and their corresponding sides will be in the same ratio.
To understand similar triangles, it is important to remember that triangles are made up of angles and sides. The angles of a triangle define its shape, while the sides determine its size. When two triangles are similar, their corresponding angles will be equal, regardless of the size or scale of the triangles.
One way to determine if two triangles are similar is by using the angle-angle similarity postulate, also known as the AA similarity postulate. According to this postulate, if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. This means that the third angle of each triangle will also be congruent.
In addition to the angle-angle similarity postulate, there are other methods to determine if two triangles are similar, such as the side-angle-side (SAS) similarity theorem and the side-side-side (SSS) similarity theorem. These theorems involve comparing both angles and sides of the triangles to establish similarity.
Understanding similar triangles is essential in geometry, as it allows for the calculation of unknown side lengths and angles. By knowing that two triangles are similar, one can use the ratios of their corresponding sides to find missing measurements. Similar triangles also play a significant role in various applications, such as navigation, architecture, and engineering.
Exploring the Parts of Similar Triangles
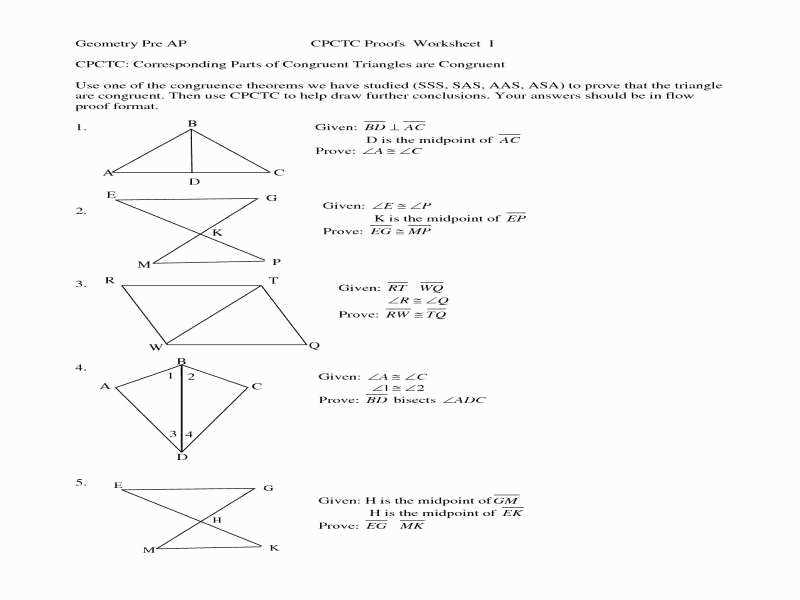
Similar triangles are an important concept in geometry. They are triangles that have the same shape but may have different sizes. It is crucial to understand the different parts of similar triangles in order to solve problems and prove mathematical theorems.
One of the key parts of similar triangles is the corresponding angles. Corresponding angles are the angles that are in the same position in each triangle. For example, if we have two similar triangles ABC and DEF, angle A corresponds to angle D, angle B corresponds to angle E, and angle C corresponds to angle F. These corresponding angles have the same measure.
Another important part of similar triangles is the corresponding sides. Corresponding sides are the sides that are in the same position in each triangle. For example, side AB corresponds to side DE, side BC corresponds to side EF, and side AC corresponds to side DF. The corresponding sides in similar triangles are proportional in length.
By understanding the concept of corresponding angles and corresponding sides in similar triangles, we can solve various problems. We can use the properties of similar triangles to find missing side lengths, determine if two triangles are similar, and prove mathematical theorems. The study of similar triangles is crucial in many areas of mathematics, such as trigonometry and geometry.
- In order to explore the concept of similar triangles further, let’s consider an example:
- We have two triangles, triangle ABC and triangle XYZ.
- Angle A is congruent to angle X, angle B is congruent to angle Y, and angle C is congruent to angle Z.
- Side AB is proportional to side XY, side BC is proportional to side YZ, and side AC is proportional to side XZ.
- These triangles are similar because their corresponding angles are congruent and their corresponding sides are proportional.
In conclusion, understanding the different parts of similar triangles, such as corresponding angles and corresponding sides, is essential in geometry. These parts allow us to solve problems and prove mathematical theorems using the properties of similarity. By exploring and mastering the concept of similar triangles, we can develop a deeper understanding of geometry and its applications in various fields.
Worksheet for Similar Triangles
In mathematics, similar triangles are triangles that have the same shape, but not necessarily the same size. This means that corresponding angles in similar triangles are equal, and the corresponding sides are proportional.
Similar triangles are important in various areas of geometry, such as trigonometry and the study of ratios. To practice identifying and working with similar triangles, students can use worksheets specifically designed for this topic.
A typical worksheet for similar triangles may include questions that ask students to determine if two triangles are similar based on given information, such as side lengths or angle measures. Students may also be asked to find missing side lengths or angle measures in similar triangles using proportions.
To solve these problems, students can use the properties of similar triangles, such as the Angle-Angle (AA) similarity postulate, the Side-Side-Side (SSS) similarity theorem, or the Side-Angle-Side (SAS) similarity theorem. These theorems and postulates provide rules for determining similarity and finding missing values.
Overall, working on a worksheet for similar triangles can help students develop their understanding of geometric concepts and improve their problem-solving skills. It allows them to practice applying theorems and postulates to real-world situations, which can be valuable in their mathematical education.
Answers and Explanations for the Worksheet
In this section, we will provide the answers and explanations for the given worksheet on parts of similar triangles. Understanding the concepts and properties of similar triangles is crucial for solving problems related to their parts.
Question 1:
In the first question, we are given two triangles, ABC and DEF, and we need to find the value of x. Looking at the diagram, we can see that triangle ABC is similar to triangle DEF since they have the same angles. According to the property of corresponding sides, we can set up the proportion:
AB/DE = BC/EF = AC/DF
Substituting the given values in the proportion, we have:
12/18 = 4/x
By cross multiplying, we get:
12x = 72
Dividing both sides by 12, we find that x = 6.
Question 2:
In the second question, we are given triangle KLM is similar to triangle NOP. We need to find the value of y. Again, using the property of corresponding sides, we set up the proportion:
KL/NO = LM/OP = KM/NP
Substituting the given values in the proportion, we have:
14/21 = 8/y
By cross multiplying, we get:
14y = 168
Dividing both sides by 14, we find that y = 12.
These are the answers and explanations for the given worksheet on parts of similar triangles. It is important to understand and apply the concepts of similarity and corresponding sides to successfully solve problems involving similar triangles.
Practice Problems for Applying Similar Triangles
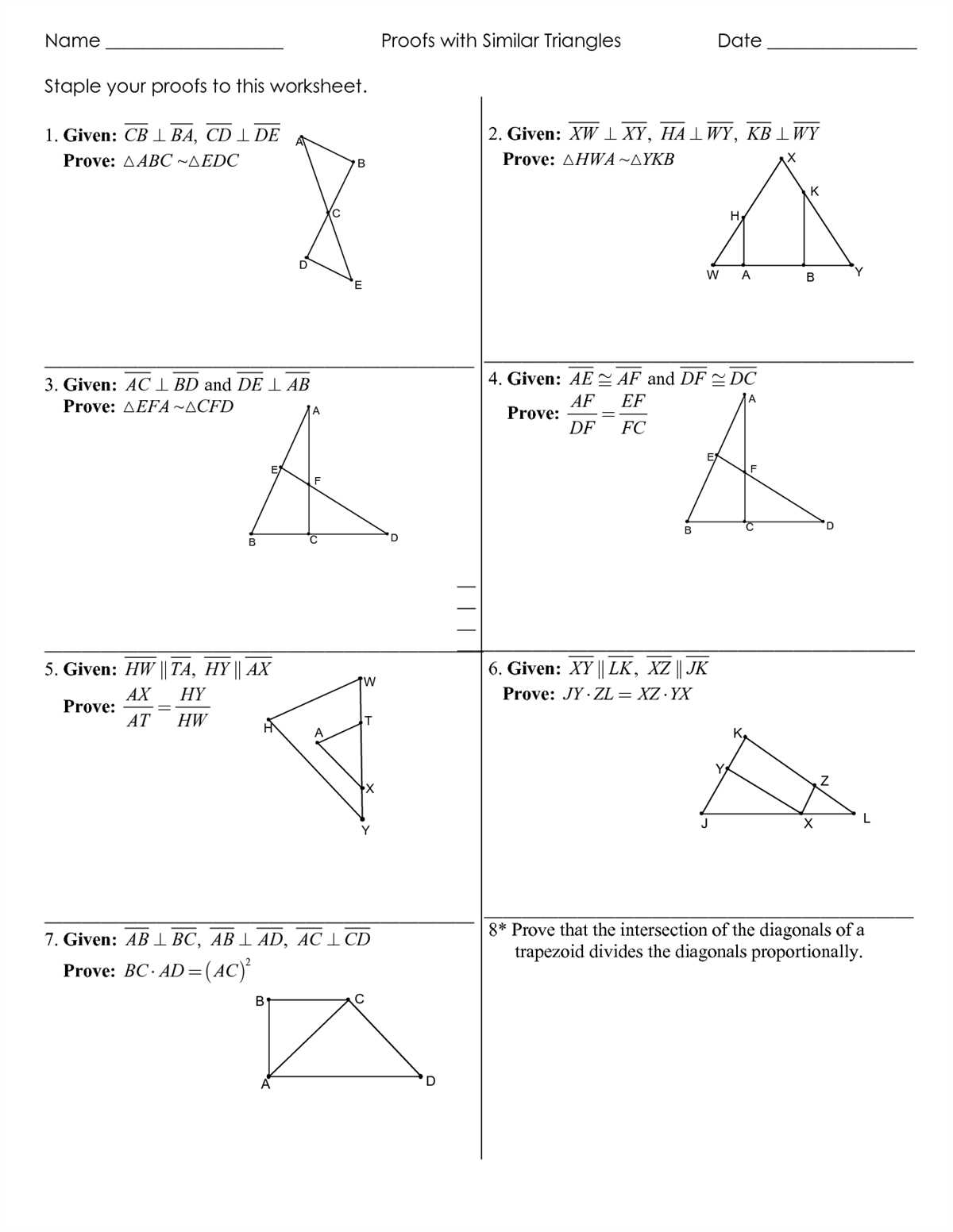
Now that we have learned about similar triangles and their properties, let’s put our knowledge into practice with some challenging problems. These problems will test your understanding of the concepts we have discussed so far. Remember to use the properties of similar triangles, such as corresponding angles and proportional sides, to solve these problems.
Here are some practice problems for you to solve:
Problem 1:
In triangle ABC, angle B is congruent to angle D. If the length of side AB is 6 cm and the length of side BC is 9 cm, find the length of side DE if triangle ADE is similar to triangle ABC.
Problem 2:
In triangle XYZ, angle X is congruent to angle Z. If the length of side XY is 12 cm and the length of side YZ is 8 cm, find the length of side AC if triangle ACZ is similar to triangle XYZ.
Problem 3:
In triangle PQR, angle P is congruent to angle R. If the length of side PQ is 15 cm and the length of side QR is 9 cm, find the length of side ST if triangle STR is similar to triangle PQR.
- Solve each problem step by step, clearly showing your work and reasoning.
- Take your time and double-check your solutions.
- If you get stuck, don’t hesitate to review the concepts and revisit the examples we covered in the previous sections.
- Once you have completed the problems, compare your answers with the given solutions to assess your understanding.
Remember, practicing similar triangle problems is essential for mastering the topic. The more practice you do, the more familiar you will become with the properties and techniques used to solve them. Good luck!