Understanding the concept of point of concurrency is crucial in the field of geometry. It is the point where three or more lines, line segments, or rays intersect. Point of concurrency worksheet answers help students practice their understanding of this important geometric concept.
This comprehensive guide provides a collection of point of concurrency worksheet answers to assist students in their learning journey. These worksheets cover various types of points of concurrency, such as the circumcenter, incenter, centroid, and orthocenter.
Each worksheet includes a set of questions that require students to apply their knowledge of point of concurrency. Students will be challenged to identify the type of point of concurrency given a diagram, find missing values related to the point of concurrency, and solve problems involving the properties of these points.
By using these point of concurrency worksheet answers, students can reinforce their understanding of this geometric concept and improve their problem-solving skills. They will gain the confidence to tackle complex geometry problems and develop a deeper understanding of the relationships between different points of concurrency.
Understanding the Concept of Point of Concurrency
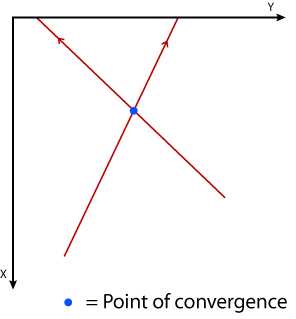
The point of concurrency is a concept in geometry that refers to the point where three or more lines, rays, or segments intersect or come together. This point is significant because it has unique properties and can be used in various geometric constructions and calculations. In particular, there are three main points of concurrency: the circumcenter, the incenter, and the centroid.
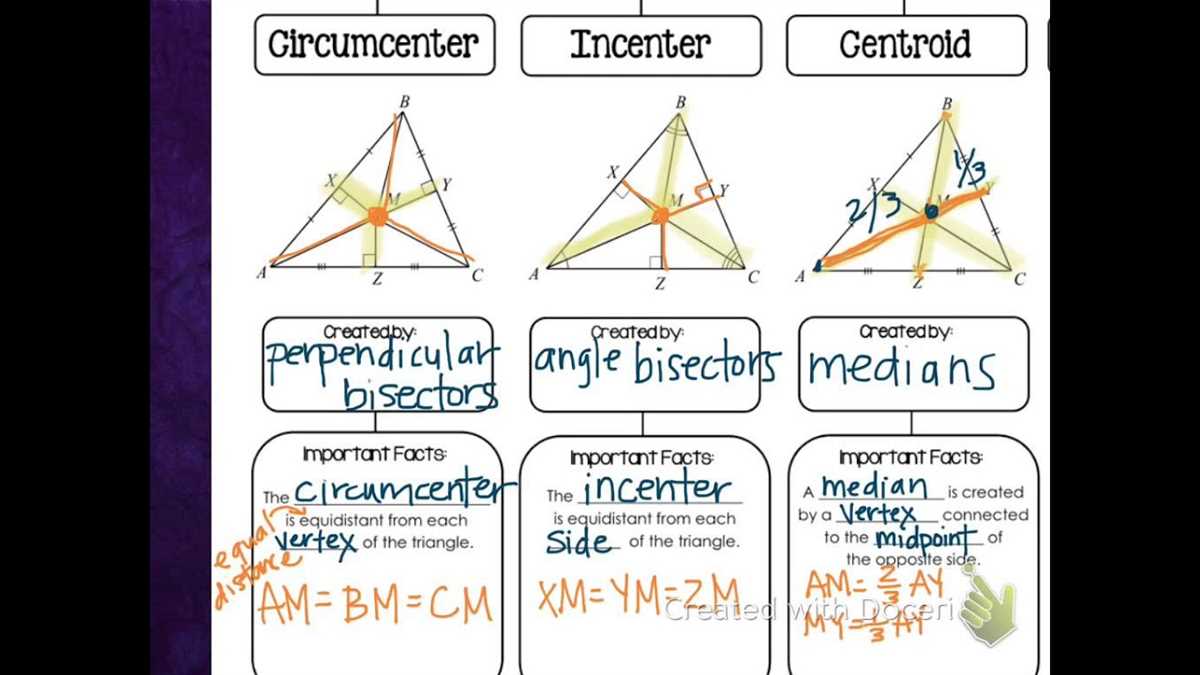
The circumcenter is the point of concurrency for the perpendicular bisectors of a triangle. It is the center of the circle that passes through all three vertices of the triangle. This point is equidistant from the three vertices, which means that the circumradius, the radius of the circumcircle, is the same for all three sides of the triangle.
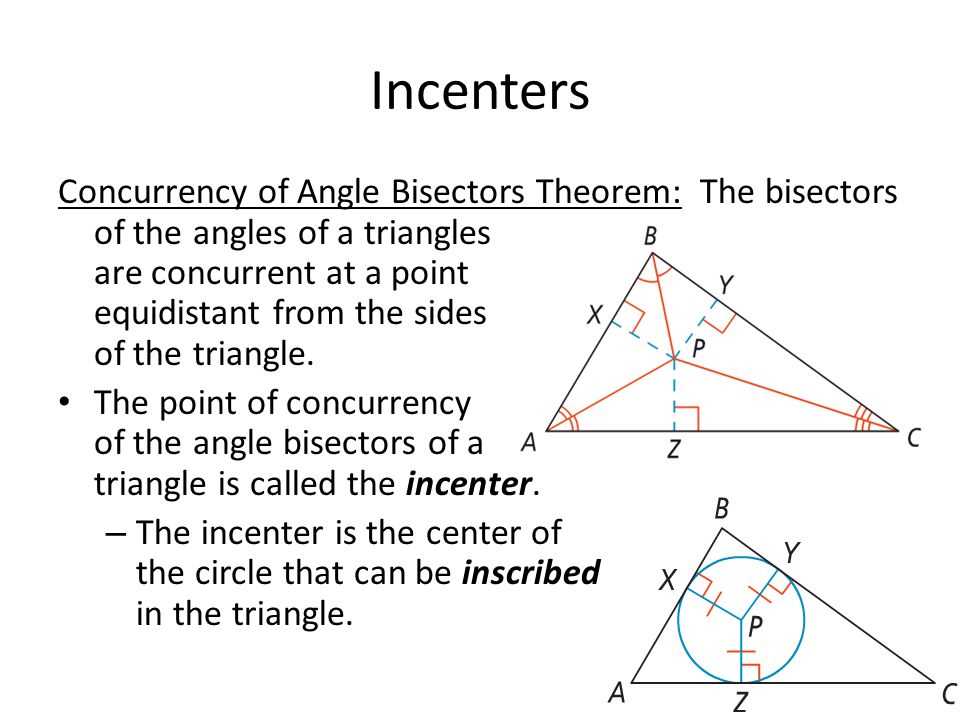
The incenter is the point of concurrency for the angle bisectors of a triangle. It is the center of the circle that is inscribed within the triangle, touching all three sides. This point is equidistant from the three sides of the triangle, which means that the inradius, the radius of the incircle, is the same for all three sides.
The centroid is the point of concurrency for the medians of a triangle. It is the point where the three medians, lines connecting each vertex to the midpoint of the opposite side, intersect. The centroid divides each median in a ratio of 2:1, with the longer segment closer to the vertex. This point is also known as the center of gravity of the triangle, as it is the balance point where the triangle would be perfectly balanced on a needle.
Understanding the concept of point of concurrency is essential in geometry as it allows for the analysis and calculation of various properties of triangles and other geometric figures. It provides a framework for solving problems and making deductions based on the relationships between different points of concurrency. By mastering this concept, students can explore and understand the intricate world of geometry with greater depth and clarity.
The Definition and Importance of Point of Concurrency
In geometry, the term “point of concurrency” refers to the point where three or more lines, rays, or line segments intersect or coincide with each other. It is a significant concept in geometry as it allows us to study the relationships and properties of geometric figures.
The point of concurrency can be located at different positions depending on the type of figures involved. For example, the point of concurrency of three lines can be found by solving their corresponding equations simultaneously. In the case of triangle, different types of points of concurrency can be identified, such as the centroid (the point of intersection of the medians), the incenter (the point of intersection of the angle bisectors), and the circumcenter (the point where the perpendicular bisectors of the sides meet).
The understanding of point of concurrency is essential in various mathematical applications. For instance, it is used in architectural design to determine the point where three or more supporting beams should intersect to provide maximum stability. It is also employed in surveying to locate the position of a specific point on the Earth’s surface by using the intersecting lines of direction. Additionally, point of concurrency plays a role in physics and engineering to analyze the forces acting on an object and calculate its equilibrium.
In conclusion, the point of concurrency is a fundamental concept in geometry that allows us to study the interactions between geometric figures. It not only helps us understand the relationships and properties of these figures but also finds practical applications in various fields. Whether it is used in architecture, surveying, or physics, the point of concurrency is an important tool for analyzing and solving problems related to the spatial relationships of objects.
Types of Concurrency in Geometry
In geometry, concurrency refers to the property of multiple lines or line segments intersecting at a common point. There are several types of concurrency that are commonly studied, including the circumcenter, incenter, centroid, and orthocenter.
Circumcenter: The circumcenter is the point of concurrency for the perpendicular bisectors of a triangle. It is equidistant from the three vertices of the triangle and is the center of the triangle’s circumcircle.
Incenter: The incenter is the point of concurrency for the angle bisectors of a triangle. It is equidistant from the three sides of the triangle and is the center of the triangle’s incircle.
Centroid: The centroid is the point of concurrency for the medians of a triangle. It is the point where the three medians intersect and is the center of gravity of the triangle.
Orthocenter: The orthocenter is the point of concurrency for the altitudes of a triangle. It is the point where the three altitudes intersect and is the center of the triangle’s circumcircle.
Table of Concurrency Types:
- Circumcenter: Point of concurrency for perpendicular bisectors
- Incenter: Point of concurrency for angle bisectors
- Centroid: Point of concurrency for medians
- Orthocenter: Point of concurrency for altitudes
These points of concurrency play an important role in geometry, as they provide valuable information about the properties and relationships of triangles. By studying the various types of concurrency, mathematicians are able to gain a deeper understanding of the geometric principles that govern our world.
Methods to Determine Points of Concurrency
Points of concurrency refer to the specific points where certain lines or segments intersect in a geometric figure. These points hold significant properties and can help us understand the relationships between different elements of the figure. There are three main methods to determine points of concurrency: the intersection of perpendicular bisectors, the intersection of angle bisectors, and the intersection of medians.
The intersection of perpendicular bisectors: The perpendicular bisectors of the sides of a triangle intersect at a single point known as the circumcenter. The circumcenter is equidistant from the vertices of the triangle and lies on the perpendicular bisectors of all three sides. It plays a crucial role in defining the properties of the triangle, such as the lengths of its sides and angles.
The intersection of angle bisectors: The angle bisectors of a triangle intersect at a single point known as the incenter. The incenter is equidistant from the three sides of the triangle and lies on the angle bisectors. It is the center of the inscribed circle, which is the largest circle that can fit inside the triangle. The incenter helps determine the properties of the triangle, such as the lengths of its sides and angles.
The intersection of medians: The medians of a triangle intersect at a single point known as the centroid. The centroid divides each median into two segments, with the segment containing the centroid being twice as long as the other segment. The centroid is the balancing point of the triangle and is also the center of mass of a triangular shape. It helps determine the stability and distribution of weight within the triangle.
By understanding and utilizing these methods, mathematicians and scientists can accurately determine the points of concurrency in various geometric figures, providing valuable insights into the properties and relationships of these shapes.
Examples of Point of Concurrency in Different Geometric Figures
In geometry, a point of concurrency refers to a point where multiple lines or line segments intersect or meet. This point is significant as it plays a crucial role in various geometric figures and constructions. Understanding and identifying these points of concurrency can help in solving geometric problems and analyzing the properties of different figures.
One of the most well-known examples of a point of concurrency is the circumcenter in a triangle. The circumcenter is the point where the perpendicular bisectors of the triangle’s sides intersect. It is equidistant from the three vertices of the triangle and is the center of the circumcircle, the circle that passes through all three vertices.
Another example is the centroid in a triangle. The centroid is the point of concurrency of the triangle’s medians. A median is a line segment joining a vertex of the triangle to the midpoint of the opposite side. The centroid divides each median into segments in a ratio of 2:1, with the longer segment closer to the vertex. It is also known as the center of gravity or geometric center of the triangle.
In a parallelogram, the point of concurrency is the intersection of the diagonals. The diagonals of a parallelogram bisect each other, meaning they divide each other into two equal parts. The point of intersection is the midpoint of both diagonals and is equidistant from all four vertices of the parallelogram.
It is important to note that different geometric figures have different types of points of concurrency. For example, in a quadrilateral, there can be multiple points of concurrency depending on the properties and shapes of the figure. Similarly, in a circle, the center is the only point of concurrency. Understanding these points and their properties is vital in geometric analysis and problem-solving.
Solutions to Point of Concurrency Worksheets
In the study of geometry, one important topic is the concept of point of concurrency. This refers to the point where three or more lines, segments, or rays intersect or meet. To understand and practice this concept, students are often given worksheets that involve finding the point of concurrency in different geometric figures.
These worksheets can be challenging, especially for students who are new to the concept. However, with enough practice and understanding of the properties of the figures involved, they can become easier to solve. Below are some solutions to common point of concurrency worksheets:
1. Circumcenter of a Triangle Worksheet:
In this worksheet, students are given a triangle and asked to find its circumcenter. The circumcenter is the point of concurrency of the perpendicular bisectors of the triangle’s sides. To find the circumcenter, students can follow these steps:
- Identify the midpoints of each side of the triangle.
- Construct perpendicular lines to each side of the triangle, passing through its corresponding midpoint.
- Find the intersection point of these perpendicular lines. This is the circumcenter.
2. Centroid of a Triangle Worksheet:
In this worksheet, students are given a triangle and asked to find its centroid. The centroid is the point of concurrency of the medians of the triangle. To find the centroid, students can follow these steps:
- Identify the midpoint of each side of the triangle.
- Construct a line segment from a vertex of the triangle to the midpoint of the opposite side.
- Repeat this process for the other two vertices of the triangle.
- Find the intersection point of these three line segments. This is the centroid.
3. Incenter of a Triangle Worksheet:
In this worksheet, students are given a triangle and asked to find its incenter. The incenter is the point of concurrency of the angle bisectors of the triangle. To find the incenter, students can follow these steps:
- Identify the angle bisectors of each angle of the triangle.
- Construct perpendicular lines to each angle bisector, passing through its corresponding vertex.
- Find the intersection point of these perpendicular lines. This is the incenter.
By practicing these worksheets and understanding the concepts behind the point of concurrency, students can develop a strong foundation in geometry and enhance their problem-solving skills.
Q&A:
What is a point of concurrency?
A point of concurrency is where three or more lines, rays, or segments intersect.
What are the different types of points of concurrency?
The different types of points of concurrency include the circumcenter, incenter, centroid, and orthocenter.
What is the circumcenter?
The circumcenter is the point of concurrency of the perpendicular bisectors of a triangle.
What is the incenter?
The incenter is the point of concurrency of the angle bisectors of a triangle.
What is the centroid?
The centroid is the point of concurrency of the medians of a triangle.