
Exponential and logarithmic functions are two important types of mathematical functions that are widely used in various fields including science, engineering, finance, and computer science. They both have unique properties and applications that make them essential in solving complex problems and modeling real-world phenomena.
An exponential function is defined as a function in which the variable appears in the exponent. It can be represented in the form f(x) = a^x, where ‘a’ is the base and ‘x’ is the exponent. These functions exhibit exponential growth or decay depending on whether the base is greater than or less than 1.
On the other hand, logarithmic functions are the inverse of exponential functions. They are defined as functions that represent the exponent to which a base must be raised to obtain a given value. Logarithmic functions are commonly represented as f(x) = logᵦ(x), where ‘x’ is the argument, ‘β’ is the base, and ‘log’ denotes the logarithm.
In this post-test, we will explore the properties and applications of exponential and logarithmic functions, and delve into solving problems related to them. By understanding the fundamental concepts of these functions, we can gain a deeper insight into the behavior of complex systems and develop powerful tools for analyzing and predicting various phenomena.
What Are Exponential and Logarithmic Functions
Exponential and logarithmic functions are important mathematical concepts that are frequently used in various fields such as physics, economics, biology, and computer science. They are both types of functions that involve exponents and logarithms, which are mathematical operations based on powers and inverse powers.
An exponential function is a function in the form of f(x) = a^x, where “a” is a positive constant called the base and “x” is the exponent. The base “a” represents the rate at which the function grows or decays, and the exponent “x” determines how many times the base is multiplied by itself. Exponential functions have a characteristic shape, with a steep growth or decay depending on the value of the base.
A logarithmic function, on the other hand, is the inverse of an exponential function. It is written as f(x) = loga(x), where “a” is the base and “x” is the value of the logarithm. Logarithmic functions can be thought of as answering the question “what power do we need to raise the base to in order to get x?” They are used to solve equations or problems involving exponential growth or decay.
Exponential and logarithmic functions are closely related and have many applications. Exponential functions are used to model population growth, compound interest, radioactive decay, and other phenomena that exhibit exponential behavior. Logarithmic functions are used in solving exponential equations, analyzing data with large ranges, and compressing information.
In conclusion, exponential and logarithmic functions are fundamental concepts in mathematics that find wide application in various fields. Understanding these functions and their properties is essential for solving problems involving exponential growth or decay, as well as analyzing data with large ranges. Exponential and logarithmic functions provide powerful tools for modeling and interpreting real-world phenomena.
Definition and Basic Properties
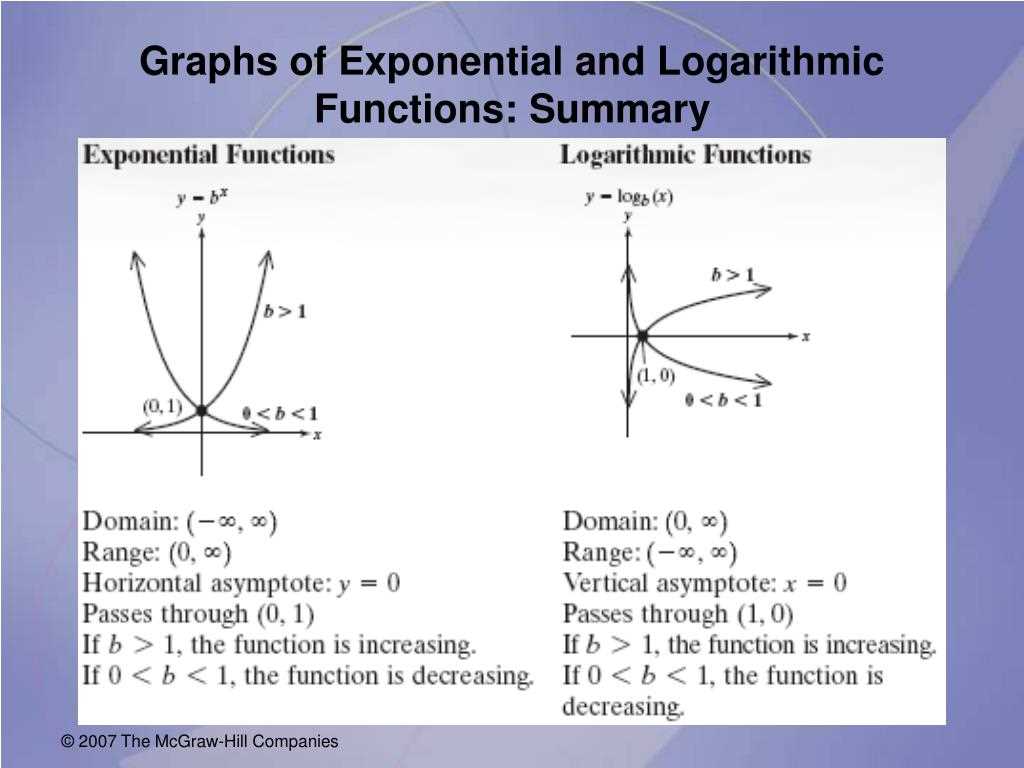
Exponential and logarithmic functions are two fundamental concepts in mathematics that are closely related to each other. An exponential function is a function of the form f(x) = a^x, where a is a positive constant called the base. The exponent x can be any real number. The logarithmic function is the inverse of the exponential function, and is defined as the function that undoes the action of exponentiation. It is denoted by the symbol log(a, x) or simply log(x) when the base is understood.
One of the key properties of exponential functions is that they grow or decay at an exponential rate. For example, if a > 1, then the function f(x) = a^x grows rapidly as x increases, while if 0 < a < 1, then the function decays rapidly as x increases. Exponential functions also have a special property called the "multiplicative property," which states that f(x + y) = f(x) * f(y), where f(x) is an exponential function.
The logarithmic function has its own set of important properties. One of the key properties is the “inverse property,” which states that log(a, f(x)) = x for any positive base a and positive value of f(x). This property allows us to convert exponential equations into logarithmic equations and vice versa. The logarithmic function also has a property called the “change of base property,” which allows us to change the base of the logarithm to any other positive base.
In summary, exponential and logarithmic functions are closely related and have many important properties. Understanding these properties is vital for solving equations, graphing functions, and applying exponential and logarithmic functions in various real-world scenarios.
Graphical Representation

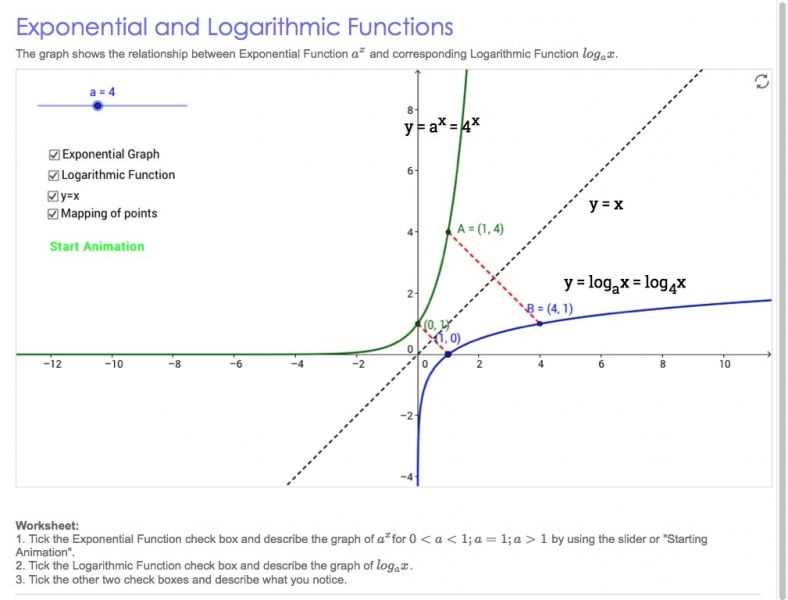
In mathematics, the graphical representation of exponential and logarithmic functions is a powerful tool for understanding their behavior and properties. Graphing allows us to visualize how these functions change over different inputs, providing insight into their rates of growth and decay.
When graphing exponential functions, the key feature to pay attention to is the steady increase or decrease in value as the input variable changes. For example, the graph of the function y = 2^x rises rapidly as x increases, showing exponential growth. On the other hand, the graph of the function y = 1/2^x decreases rapidly as x increases, indicating exponential decay.
Logarithmic functions, on the other hand, exhibit the opposite behavior. The graph of a logarithmic function is a curve that becomes steeper as the input variable increases. For instance, the graph of the function y = log(x) gradually rises when x is small, but its rate of increase becomes more significant as x grows larger.
Understanding the graphical representation of exponential and logarithmic functions is crucial for various applications in fields such as finance, physics, and biology. For instance, in finance, exponential functions can model compound interest or population growth. Logarithmic functions are essential for analyzing exponential decay, such as radioactive decay or the rate at which a drug metabolizes in the body.
In conclusion, graphical representation helps us visualize the behavior of exponential and logarithmic functions, providing insights into their rates of growth or decay. By graphing these functions, we can better understand their properties and use them to model real-world phenomena.
Exponential Growth and Decay
The concept of exponential growth and decay is a fundamental idea in mathematics and is widely applicable in various fields such as biology, economics, and population studies. Exponential growth refers to the rapid increase in quantity or value over time, while exponential decay refers to the rapid decrease.
In exponential growth, the quantity or value doubles or increases at a constant rate over a given period. The growth rate is determined by the value of the base of the exponential function. For example, if the base is 2, the quantity will double with each successive period. This type of growth is often observed in biological populations, compound interest calculations, and technological advancements.
On the other hand, exponential decay occurs when the quantity or value decreases or decays at a constant rate over time. The decay rate is determined by the value of the base of the exponential function, which is typically less than 1. For instance, if the base is 0.5, the quantity will halve with each successive period. This type of decay is seen in radioactive decay, depreciation of assets, and natural phenomena.
Exponential growth and decay can be described using exponential functions, which take the form y = ab^x, where a represents the initial value, b represents the growth or decay factor, and x represents the time or period.
Understanding the concepts and applications of exponential growth and decay is crucial in various fields for predicting trends, making calculations, and analyzing data. It allows researchers, economists, and scientists to model and understand the behavior of complex systems over time.
Logarithmic Functions and Their Applications
Logarithmic functions are mathematical functions that are the inverse of exponential functions. They are widely used in various fields of study and have numerous practical applications.
Understanding Logarithmic Functions
A logarithmic function is written as y = logb(x), where b is the base of the logarithm. The logarithm of a number x to the base b is the exponent to which b must be raised to obtain x. In other words, the logarithm of x is the power to which b needs to be raised to result in x.
Logarithmic functions are extremely useful in situations where the rate of growth or decay of a quantity is not constant, but rather changes exponentially. The logarithmic scale allows us to make sense of and analyze such data.
Applications of Logarithms
- Finance: Logarithmic functions are used in finance to model the growth of investments, compound interest, and time value of money.
- Acoustics: Logarithmic functions are used to measure and analyze sound intensity and decibel levels.
- Chemistry: Logarithmic functions are used in pH calculations and to describe reaction rates in chemical kinetics.
- Computer Science: Logarithmic functions are used in algorithms and data structures to optimize performance and efficiency.
- Signal Processing: Logarithmic functions are used to compress and expand audio signals and in image processing techniques such as dynamic range compression.
These are just a few examples of how logarithmic functions are applied in different fields. Logarithms play a vital role in many areas of science, engineering, and technology, allowing us to understand and analyze complex phenomena with exponential characteristics.
Properties and Manipulations of Exponential and Logarithmic Functions
Exponential and logarithmic functions are powerful mathematical tools that can be used to describe and analyze a wide range of phenomena in various fields, such as science, finance, and engineering. These functions exhibit several important properties and can be manipulated in different ways to solve problems and make predictions.
Properties of Exponential Functions

1. Exponential Growth and Decay: Exponential functions can model both growth and decay processes. When the growth factor is greater than 1, the function represents exponential growth, and when it is between 0 and 1, it represents exponential decay.
2. Exponential and Constant Factors: Exponential functions exhibit the property that multiplying the argument by a constant factor results in a new exponential function with a changed growth factor. This property is commonly used in situations where the growth or decay rate needs to be adjusted.
3. Exponential Function Inverses: The inverse of an exponential function is a logarithmic function. This relationship between exponential and logarithmic functions allows for solving equations involving exponential functions using logarithmic properties.
Properties of Logarithmic Functions
1. Logarithmic Scale: Logarithmic functions provide a useful way to represent and analyze data that spans several orders of magnitude. The logarithmic scale compresses large numbers, making it easier to compare and interpret data.
2. Logarithmic Laws: Logarithms follow several important properties, such as the logarithmic laws of addition, subtraction, and multiplication. These laws allow for simplifying and manipulating logarithmic expressions to solve equations or simplify calculations.
3. Logarithmic and Exponential Function Inverses: As mentioned earlier, logarithmic functions are the inverse of exponential functions. This duality allows for converting between logarithmic and exponential forms and solving equations that involve both types of functions.
Manipulations of Exponential and Logarithmic Functions

1. Exponential and Logarithmic Identities: The properties of exponential and logarithmic functions can be combined to derive important identities, such as the inverse property, the product property, and the power property. These identities allow for simplifying complex expressions involving both types of functions.
2. Solving Exponential and Logarithmic Equations: Exponential and logarithmic equations can be solved by applying the properties and manipulations of the respective functions. By using logarithms to convert exponential equations into logarithmic form, or vice versa, equations can be rearranged to find the desired solution.
3. Applications in Real-World Problems: Exponential and logarithmic functions are widely used to model and analyze real-world phenomena, such as population growth, compound interest, radioactive decay, and signal processing. By understanding the properties and manipulations of these functions, we can make accurate predictions and solve practical problems.
In summary, exponential and logarithmic functions possess important properties that make them versatile tools in various fields of study. By understanding these properties and manipulations, we can effectively analyze and solve problems involving exponential and logarithmic functions, as well as interpret and predict real-world phenomena.