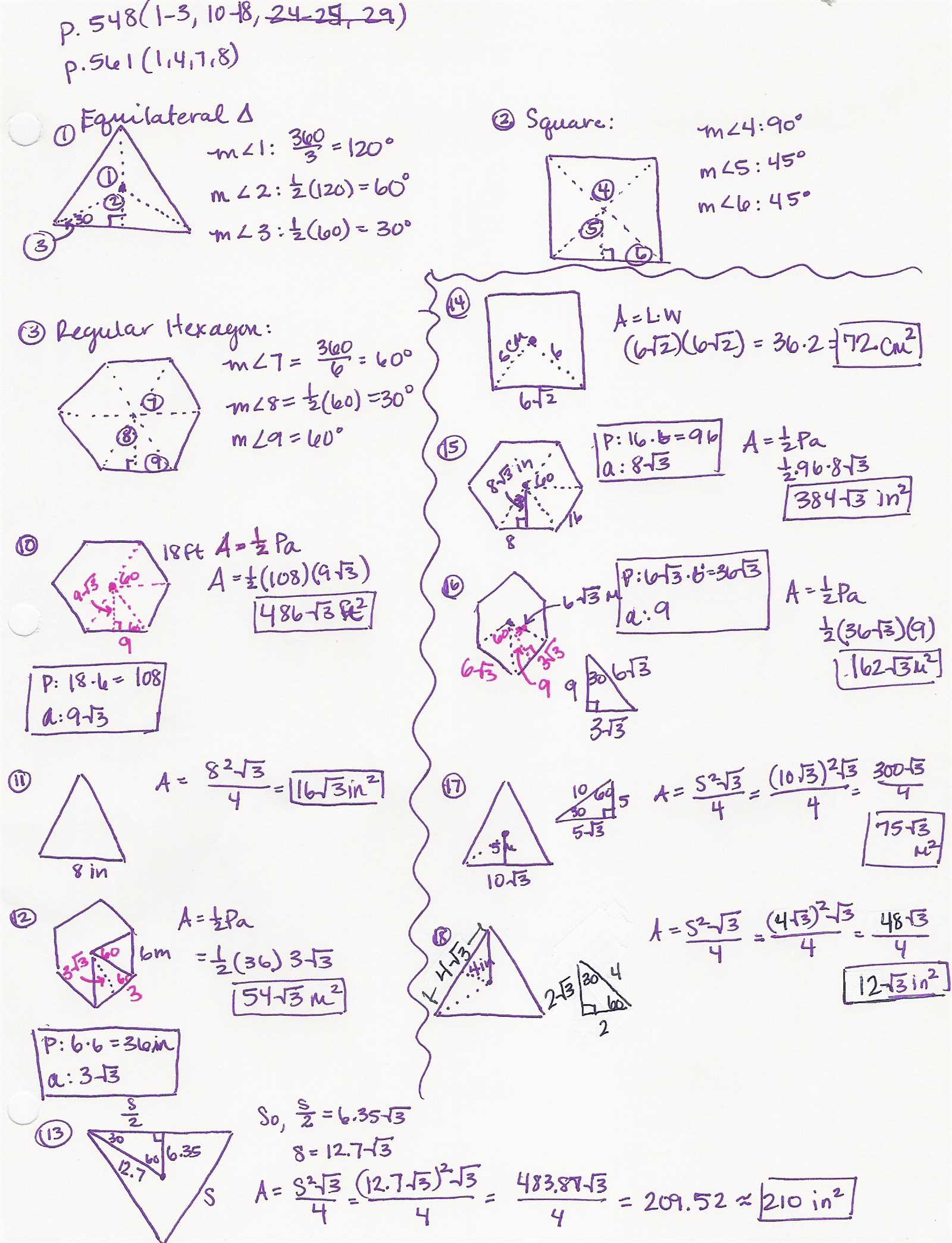
Understanding the core principles of mathematics is crucial for mastering any subject, especially when it comes to tackling complex problems. The skills you develop will not only help you pass assessments but also build a strong foundation for future learning. Focusing on the right approach can make all the difference in achieving success.
By focusing on key concepts and practicing problem-solving strategies, you can increase your confidence and improve your results. This guide aims to provide you with a comprehensive understanding of the material and offer practical solutions that will enhance your learning process. Whether you’re looking to reinforce your knowledge or tackle more challenging topics, these resources will support your growth.
Every learner faces obstacles along the way, but persistence and the right methods can turn difficulties into opportunities for improvement. It’s important to stay focused and stay committed to your studies, making sure that each step you take brings you closer to your goals. Let’s dive into the most effective ways to excel in this area of study.
Overview of Essential Mathematical Concepts
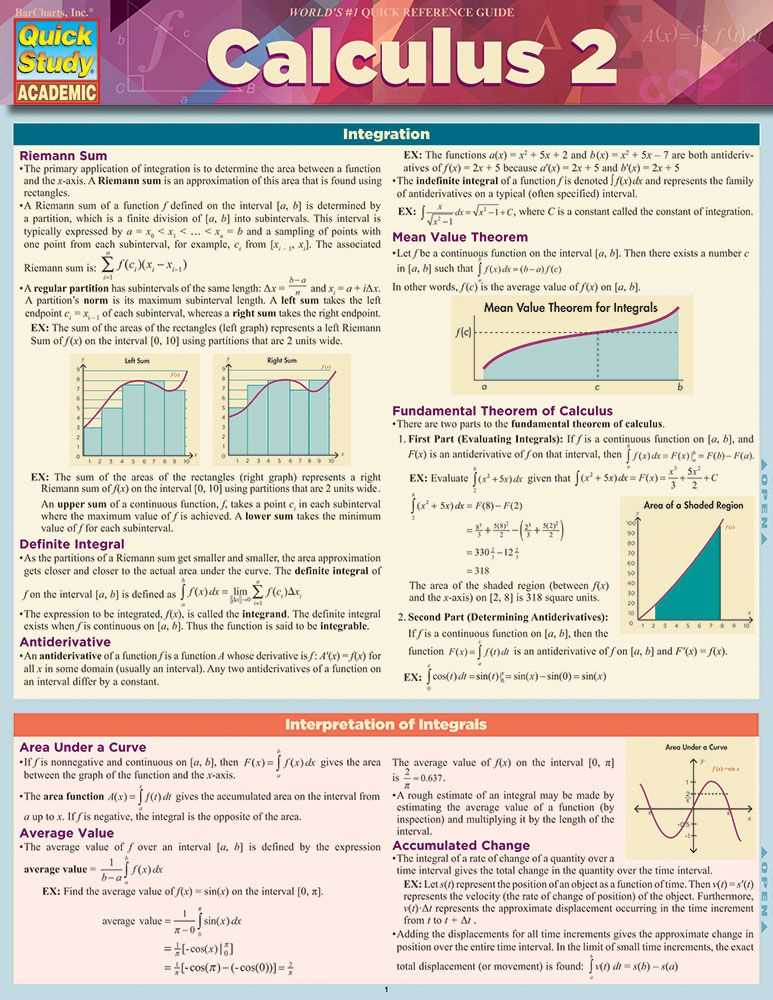
Understanding the core topics covered in this section is key to performing well in any related assessment. The focus lies on strengthening problem-solving abilities and grasping complex mathematical ideas. With the right foundation, tackling advanced exercises becomes a manageable task.
Throughout this segment, learners will encounter various types of problems designed to test their comprehension of essential principles. These problems span multiple difficulty levels, allowing individuals to challenge their knowledge while reinforcing their understanding of the material.
Effective preparation requires not only solving individual exercises but also connecting concepts and recognizing patterns across different types of problems. This approach ensures a deeper understanding, enabling individuals to navigate through questions with ease and confidence.
Anticipating potential challenges and knowing how to approach different types of problems will be highly beneficial in achieving success. Emphasizing key ideas and regularly practicing will help you master the material and improve your performance when evaluating your knowledge.
Understanding Key Concepts in Chapter 2
Mastering the foundational ideas in this section is critical for successfully navigating more advanced topics. A strong grasp of these core principles will not only support your problem-solving ability but also enhance your analytical thinking. Each concept builds on the previous, creating a structure that enables you to tackle more complex problems with ease.
In this part of the material, the main focus is on understanding relationships and applying formulas to solve practical problems. Recognizing how these concepts interconnect is essential for both theoretical understanding and real-world application.
| Concept | Description |
|---|---|
| Functions | Explore different types of functions and their properties, including linear, quadratic, and polynomial functions. |
| Equations | Learn to manipulate and solve various equations, such as linear and exponential equations. |
| Graphing Techniques | Understand the methods for graphing functions and interpreting their graphical behavior. |
| Systems of Equations | Analyze how to solve systems of equations using substitution and elimination methods. |
Grasping these key ideas will prepare you for more advanced topics, ensuring you have the necessary skills to approach new challenges with confidence.
Step-by-Step Guide to Problem Solutions
Breaking down complex problems into smaller, manageable steps is key to finding the correct solution. This approach not only helps you understand the reasoning behind each step but also ensures you don’t overlook important details. A methodical process will guide you through even the most difficult exercises.
Step 1: Identify the Problem
The first step in any problem-solving process is to fully understand what is being asked. Read the problem carefully and identify the given information and what needs to be determined. This will lay the foundation for your approach.
Step 2: Organize and Apply Formulas
Once you have a clear understanding of the problem, organize the known values and choose the appropriate formulas. Remember, different types of problems require different strategies. Be sure to apply the right method for each specific situation to avoid unnecessary complications.
Accuracy in following each step is essential. By carefully working through each part of the problem, you will build a solid understanding of how to approach future challenges with confidence.
Common Mistakes in Mathematical Assessments

Even experienced learners can make errors when solving mathematical problems, especially when under time pressure. Recognizing these common mistakes is essential for improving your accuracy and performance. Often, the key to success lies in avoiding small missteps that can significantly affect the final outcome.
One frequent mistake is misinterpreting the problem. Failing to fully understand what is being asked can lead to incorrect approaches. It’s important to carefully read the question and identify the key elements before proceeding.
Another common issue is rushing through calculations. Skipping steps or not double-checking the work can result in simple arithmetic mistakes that can throw off the entire solution. Taking the time to verify each step ensures better accuracy and avoids these errors.
By being mindful of these pitfalls and adopting a more careful, methodical approach, learners can significantly reduce mistakes and improve their results on mathematical assessments.
How to Improve Your Scores
Achieving higher scores in assessments requires both strategic preparation and a consistent approach to learning. It’s not just about understanding the material, but also about how you engage with it. By refining your study habits and adopting effective techniques, you can see noticeable improvements in your performance.
Develop a Study Routine
Consistency is key when it comes to mastering any subject. Set aside dedicated time each day to review material, practice problems, and reinforce concepts. A well-structured study schedule helps ensure steady progress and reduces last-minute stress.
Focus on Weak Areas
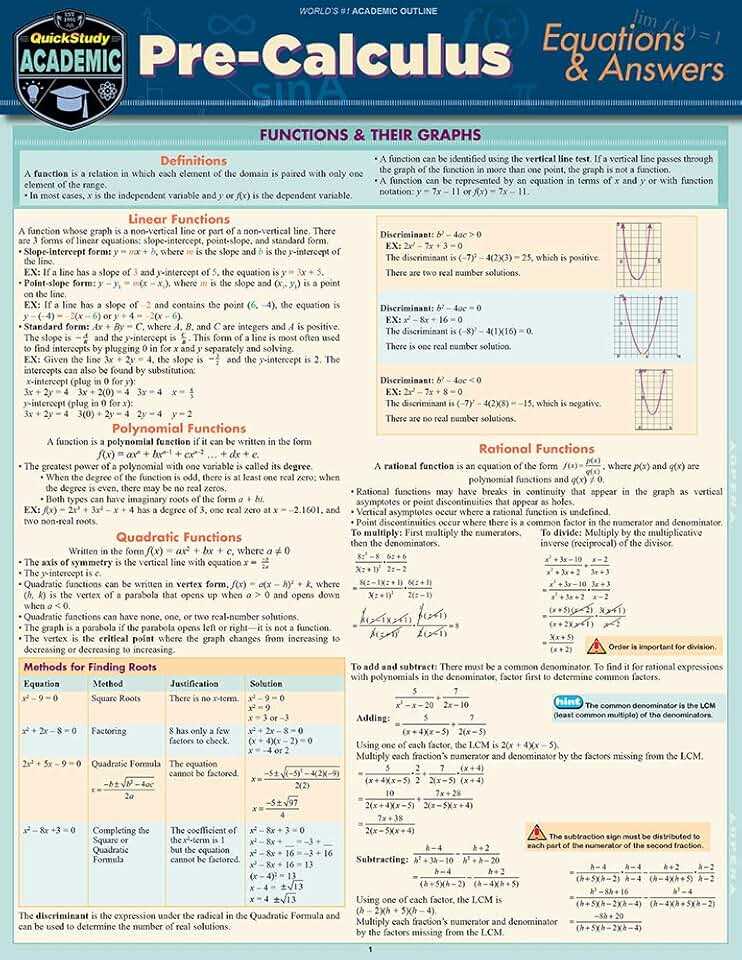
Identify the topics where you struggle the most and allocate extra time to review them. By targeting your weaknesses, you’ll build a stronger foundation and approach problems with more confidence. Don’t hesitate to seek help or use additional resources to improve your understanding.
Implementing these strategies will gradually improve your comprehension, reduce errors, and help you achieve better results in future assessments.
Useful Resources for Mathematical Preparation
Having access to the right materials is essential for enhancing your understanding of mathematical concepts and improving your skills. Utilizing a variety of resources can help you reinforce what you’ve learned and provide additional support when tackling more challenging topics. Here are some valuable tools that can assist you in your preparation.
- Textbooks and Study Guides: Well-structured books offer clear explanations and step-by-step solutions. Look for guides that include practice exercises to test your understanding.
- Online Tutorials and Courses: Many platforms provide free or paid courses tailored to different skill levels. These resources often include video lessons, quizzes, and interactive content to reinforce key ideas.
- Practice Problem Sets: Regularly working through problems is essential for building confidence. Websites like Khan Academy and other educational platforms offer a wide variety of exercises with instant feedback.
- Math Forums and Discussion Groups: Engaging with a community of learners can help clarify difficult topics. Platforms like Stack Exchange or Reddit allow users to ask questions and share insights.
By utilizing these resources and practicing regularly, you can develop a strong foundation and approach problems with greater confidence and clarity.
Tips for Effective Test-Taking Strategies
Maximizing your performance during assessments requires more than just understanding the material; effective strategies can make a significant difference in how well you manage time, reduce anxiety, and showcase your skills. By applying a thoughtful approach to your study and approach on the day of the assessment, you can improve both your focus and results.
Before the Assessment
- Review Key Concepts: Focus on the most important areas of the material and ensure you are familiar with common problem types.
- Practice Under Timed Conditions: Simulate real exam conditions by timing yourself during practice sessions to improve your speed and manage time effectively.
- Organize Study Materials: Ensure all notes, formulas, and practice problems are readily available to help with quick review and easy reference.
During the Assessment
- Read Instructions Carefully: Take time to fully understand each question before starting, and pay attention to key instructions or restrictions.
- Manage Time Wisely: Allocate time based on the complexity of the question. Avoid spending too much time on any single problem.
- Double-Check Your Work: If time permits, review your answers to ensure you haven’t missed any details or made simple mistakes.
By adopting these strategies, you can approach your assessments with confidence and efficiency, boosting your chances of success.