
In mathematics, understanding the foundational principles is crucial for solving complex problems and achieving success. The second unit of this subject often covers a variety of concepts that require both theoretical knowledge and practical application. Students are expected to grasp key techniques, recognize patterns, and apply formulas accurately to address a wide range of challenges.
Effective preparation involves more than just memorizing formulas; it requires developing a deep understanding of the underlying relationships between different concepts. As you progress through the material, you’ll encounter various problem-solving strategies that help build confidence and proficiency.
In this guide, we will walk through some of the most important topics in the unit, providing detailed solutions and explanations to help reinforce your understanding. Whether you’re looking to review material, practice specific problems, or improve your approach to tackling assignments, this resource will serve as a valuable tool for mastering the material and excelling in assessments.
Understanding Key Concepts in Advanced Math
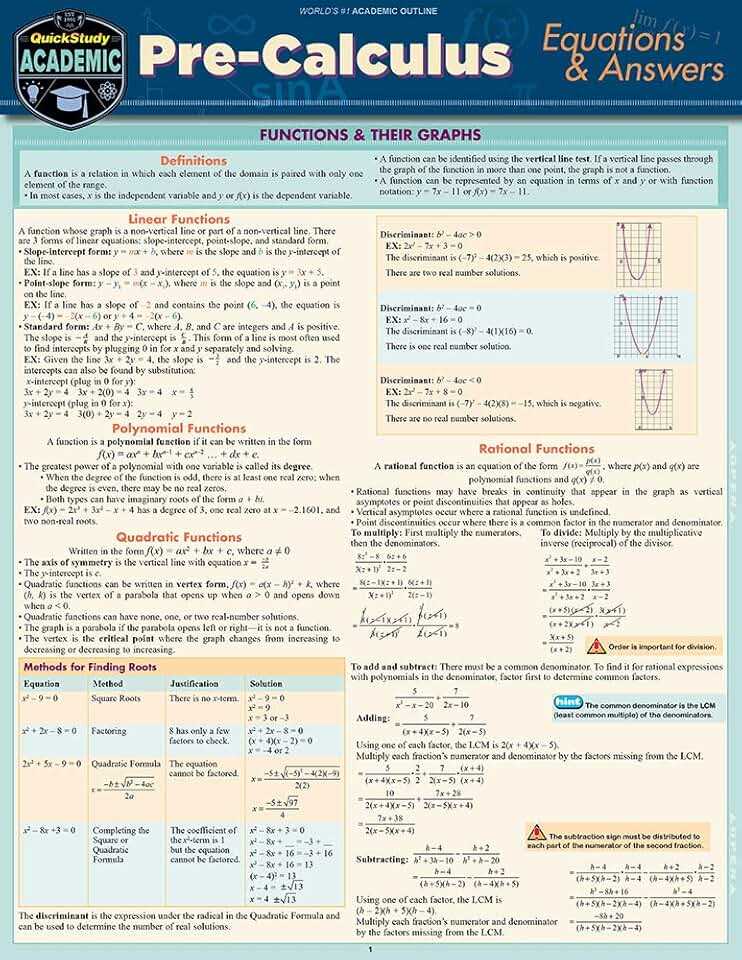
Mastering the material in the second unit is essential for building a strong foundation in this subject. The concepts introduced here are vital for understanding more complex topics in the future. To excel, it’s important to approach these ideas with a clear understanding of their applications and how they relate to one another.
One of the core areas covered in this section is the manipulation of mathematical expressions and equations. It’s necessary to be able to work with various forms and structures to solve problems efficiently. Here are some key ideas to focus on:
- Algebraic techniques: Simplifying expressions, factoring, and solving for unknowns.
- Functions: Understanding the behavior of different types of functions and their graphs.
- Equations: Mastering linear, quadratic, and other types of equations.
- Systems of equations: Solving multiple equations simultaneously using various methods.
- Rational expressions: Simplifying and solving problems involving fractions and ratios.
When you understand these concepts in depth, you’ll be able to approach problems with more confidence. Each topic builds on the previous one, so taking the time to fully grasp the foundational ideas will make advanced topics easier to tackle.
Common Mistakes in Advanced Math Assessments

When preparing for assessments, it’s easy to overlook some of the most common pitfalls that can affect performance. Understanding and recognizing these frequent errors can help you avoid them and improve your results. Many of these mistakes stem from misunderstandings of fundamental concepts or rushing through problems without careful thought.
Here are some of the most typical errors students make:
| Common Mistake | Cause | How to Avoid |
|---|---|---|
| Incorrectly simplifying expressions | Forgetting to apply rules of exponents or algebraic manipulation | Double-check every step, especially when simplifying terms |
| Misinterpreting the problem | Rushing or not fully reading the instructions | Take time to read and understand each question carefully |
| Sign errors | Confusing positive and negative signs in calculations | Carefully track signs in every equation and solution step |
| Overlooking units and variables | Not paying attention to the context of the problem | Always ensure you understand the meaning of each variable and unit |
| Skipping steps in complex problems | Trying to solve problems too quickly without showing work | Write out every step, even if it seems unnecessary |
Avoiding these common mistakes requires attention to detail and careful practice. By taking your time and reviewing your work, you can improve your accuracy and boost your confidence when facing future challenges.
Key Strategies for Test Preparation
Effective preparation for assessments involves more than simply reviewing the material. It’s about developing a strategic approach that allows you to understand the content deeply, practice solving problems, and manage your time efficiently during the exam. By implementing the right strategies, you can ensure you’re fully prepared and confident when the day arrives.
Review the Basics and Focus on Core Concepts

Start by revisiting the foundational principles that are central to the subject. These core concepts often serve as the building blocks for more advanced problems. Strengthen your understanding of key techniques, such as manipulating equations, graphing functions, and solving inequalities. The more comfortable you are with the basics, the easier it will be to tackle more complex challenges.
Practice with Purpose
Consistent practice is crucial to mastering any subject. Focus on solving a variety of problems, including those you find challenging. Work through sample exercises from textbooks, past assessments, or online resources. This hands-on approach will not only reinforce your knowledge but also help you identify areas where you may need further improvement. Simulating test conditions can also help you manage time effectively during the actual assessment.
By following these strategies, you’ll be able to approach the material with a clear plan and a higher level of preparedness, increasing your chances of success when it matters most.
How to Approach Chapter 2 Problems
When tackling problems in this section, it’s essential to follow a structured approach that allows you to break down complex questions into manageable steps. The goal is to understand the underlying concepts and apply the appropriate methods to find the solution. By staying organized and focused, you can efficiently work through each problem with confidence.
Start by carefully reading the problem to identify what is being asked. Pay attention to key details such as variables, equations, and any specific instructions. Once you have a clear understanding, determine which strategies or formulas are needed to solve the problem. Approach each question methodically, avoiding any rush to jump to conclusions.
Next, apply the relevant techniques while keeping track of each step. It’s often helpful to work through problems visually, such as drawing graphs or charts when necessary. Double-check your calculations and ensure you’ve answered the question completely, as sometimes solutions can be incorrect due to minor mistakes in reasoning or arithmetic.
Finally, practice regularly to refine your approach. The more problems you solve, the more familiar you’ll become with common patterns and techniques, helping you become more efficient in future tasks.
Step-by-Step Guide to Solutions
Solving problems in this section requires a methodical approach, ensuring that each step is completed with care to avoid mistakes. By breaking down the process into clear, manageable stages, you can confidently work through even the most challenging questions. This guide will walk you through a systematic approach to finding accurate solutions.
Understand the Problem and Identify Key Information

Before diving into calculations, take a moment to read through the problem carefully. Identify the variables, constants, and what the question is asking. Understanding the context of the problem will allow you to choose the right approach for solving it. Highlight important numbers or expressions that will help guide your work.
Apply Relevant Methods and Solve Step-by-Step

Once you’ve understood the problem, begin applying the relevant techniques. Start with basic operations such as simplifying expressions, factoring, or solving simple equations. Then, use advanced methods such as graphing or substitution when necessary. Always take your time to check each calculation as you go.
Once you reach a solution, review it to ensure all steps are logically sound. If possible, double-check the results by substituting your solution back into the original problem to confirm its accuracy.
By following this structured approach, you will not only solve the problem efficiently but also improve your ability to tackle similar questions in the future.
Importance of Practice for Success
Mastering any subject requires consistent effort, and regular practice is the key to developing both skill and confidence. Solving a variety of problems helps reinforce the concepts learned and allows you to become more comfortable with different types of questions. The more you practice, the easier it becomes to recognize patterns and apply the right strategies to solve problems quickly and accurately.
Practice helps in building familiarity with the material, enabling you to tackle challenges with ease. It also allows you to identify areas where you may need improvement. By focusing on these weaker areas and repeatedly practicing them, you can turn potential weaknesses into strengths.
Additionally, regular problem-solving enhances your ability to think critically and approach complex questions with a clear, methodical mindset. With each practice session, you increase your chances of success by reinforcing your knowledge and boosting your problem-solving efficiency.
Ultimately, continuous practice is essential for mastering any skill. Whether reviewing basic principles or tackling more advanced problems, it is the consistent effort that will lead to success when it matters most.