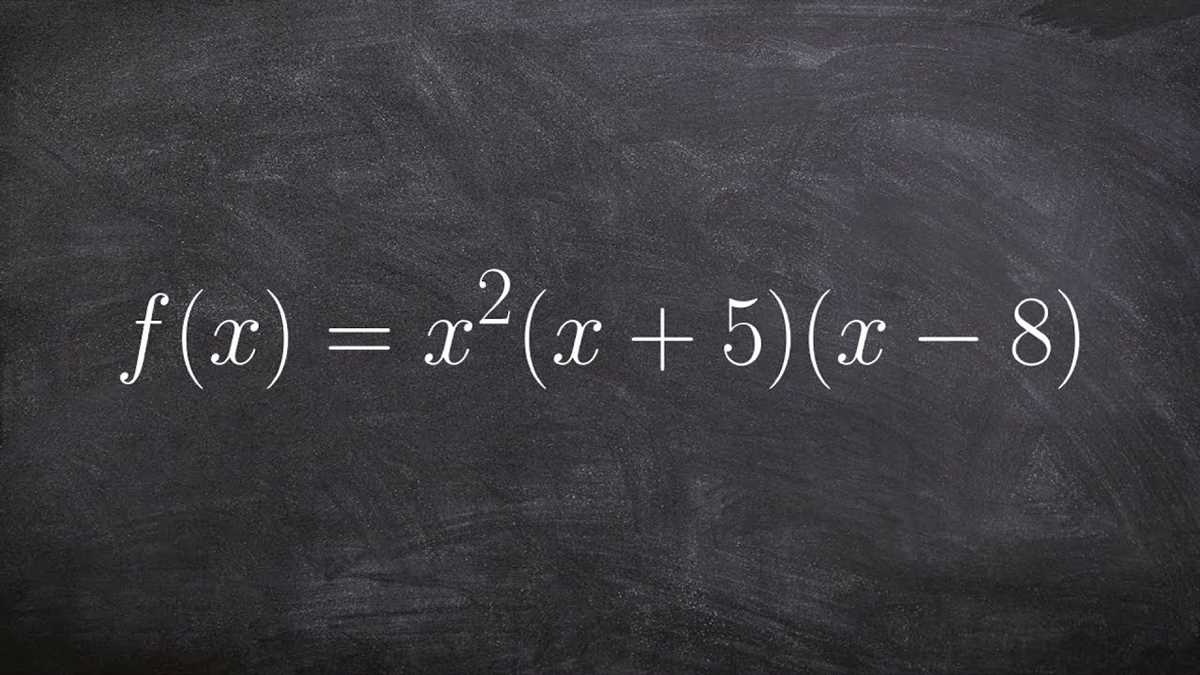
In mathematics, polynomials are one of the fundamental concepts. They are expressions consisting of variables and coefficients, combined using operations like addition, subtraction, multiplication, and division. Polynomials can have multiple terms and powers, which can make them quite complex. The process of classifying and simplifying polynomials involves organizing them according to their degree and standard form.
When classifying polynomials, we look at their degree, which is the highest power of the variable in the polynomial. For example, a polynomial with the highest power being 2 is called a quadratic polynomial, while a polynomial with the highest power being 3 is called a cubic polynomial. By determining the degree of a polynomial, we can categorize it into different types.
Simplifying polynomials involves combining like terms and reducing the polynomial to its simplest form. Like terms are terms that have the same variables and powers. By combining like terms, we can eliminate redundant expressions and make the polynomial easier to work with. Simplifying polynomials is essential for solving equations, graphing, and performing various algebraic operations.
What is Quiz 7: Classifying and Simplifying Polynomials

Quiz 7: Classifying and Simplifying Polynomials is an assessment that tests students’ understanding and proficiency in classifying and simplifying polynomial expressions. This quiz is usually given in a mathematics course, particularly in algebra or precalculus.
The quiz consists of a series of questions that require students to classify polynomials based on their degree and number of terms, as well as to simplify polynomial expressions by combining like terms and performing arithmetic operations. It may also include questions on factoring and expanding polynomials.
To successfully complete this quiz, students must have a solid understanding of polynomial concepts, such as monomials, binomials, trinomials, and polynomials of higher degrees. They should also be familiar with the rules of combining like terms, performing addition, subtraction, multiplication, and division of polynomials, and identifying the degree and number of terms in polynomial expressions.
Classifying and simplifying polynomials is an essential skill in algebra and higher-level math courses, as it forms the foundation for solving equations and working with polynomial functions. The quiz serves as an assessment tool for both students and teachers to gauge students’ understanding of these concepts and identify areas that may need further review or instruction.
Overall, Quiz 7: Classifying and Simplifying Polynomials is a crucial evaluation in a mathematics course, designed to assess students’ proficiency in classifying and simplifying polynomial expressions and ensure that they have a solid foundation in these concepts as they progress in their mathematical education.
Overview of Classifying and Simplifying Polynomials
A polynomial is an algebraic expression that consists of variables, coefficients, and exponents. These expressions can have multiple terms, which are often combined using addition and subtraction. Polynomials are an essential part of algebra and are used in various mathematical operations and problem-solving.
When classifying polynomials, they can be categorized based on the number of terms they have. A polynomial with one term is called a monomial, while a polynomial with two terms is called a binomial. Polynomials with three terms are known as trinomials, and those with more than three terms are referred to as polynomials with a specific number of terms.
To simplify polynomials, various techniques can be used depending on the specific problem. One common method is combining like terms, which involves adding or subtracting terms with the same variable and exponent. This simplification process helps to reduce the complexity of the polynomial and make it easier to work with.
Another technique for simplifying polynomials is factoring. Factoring involves breaking down a polynomial into its constituent terms or factors. This process can help in identifying common factors and simplifying the polynomial expression. Factoring is particularly useful when trying to solve equations or find roots of polynomials.
- Classification of polynomials based on the number of terms:
- Monomial: 5x^2
- Binomial: 3x + 2
- Trinomial: 2x^2 + 4x – 1
- Polynomial with four terms: 4x^3 + 3x^2 – 2x + 1
- Example of simplifying a polynomial by combining like terms:
- Original polynomial: 2x^2 + 3x^2 + 4x^2 – 5x
- Simplified polynomial: 9x^2 – 5x
- Example of simplifying a polynomial by factoring:
- Original polynomial: x^2 + 6x + 9
- Simplified polynomial: (x + 3)(x + 3) or (x + 3)^2
Overall, classifying and simplifying polynomials are essential skills in algebra that help in solving equations, graphing functions, and understanding mathematical relationships. These techniques provide a foundation for further mathematical studies and applications.
Importance of Understanding Polynomials
Polynomials are a fundamental concept in mathematics that play a significant role in various fields including algebra, calculus, and physics. Understanding polynomials is essential for both academic and real-world applications.
1. Problem-solving tool: Polynomials provide a powerful tool for solving a wide range of mathematical problems. They allow us to manipulate and model complex relationships between variables, making it easier to analyze and solve equations. Whether it’s finding the roots, graphing the function, or simplifying expressions, a solid understanding of polynomials is crucial for problem-solving.
2. Mathematical foundation: Polynomials form the building blocks of algebraic expressions. They help us understand and explore the fundamental concepts of algebra, such as addition, subtraction, multiplication, and division. By studying polynomials, students develop a solid foundation for more advanced mathematical topics like calculus and linear algebra.
3. Real-world applications: Polynomials have numerous applications in the real world. They are used to model and analyze data, make predictions, and solve real-life problems. For example, polynomials are used in physics to describe motion, in economics to model business trends, and in engineering to design and optimize structures. Having a strong grasp of polynomials allows us to apply mathematical concepts to practical situations.
4. Career opportunities: Understanding polynomials opens up exciting career opportunities in fields like engineering, computer science, finance, and research. Many professions require a solid understanding of mathematical concepts, and polynomials are often a fundamental component of these concepts. By mastering polynomials, individuals can pursue careers that involve analyzing data, developing algorithms, designing systems, and making informed decisions based on mathematical models.
In conclusion, understanding polynomials is of utmost importance in the world of mathematics and beyond. It serves as a problem-solving tool, forms the foundation for advanced math topics, has real-world applications, and can lead to exciting career opportunities. Whether you’re a student learning algebra or a professional working in a math-related field, a solid understanding of polynomials is essential for success.
Tips for Classifying Polynomials
Classifying polynomials is an essential skill in algebra. By understanding the various types of polynomials, you can effectively solve and simplify complex equations. Here are some tips to help you classify polynomials:
1. Identify the highest degree of the polynomial
Start by determining the degree of the polynomial, which is the highest power of the variable. This will give you an idea of the overall complexity of the polynomial.
2. Recognize the type of polynomial
Polynomials can be classified into different types based on their number of terms. For example, a polynomial with one term is called a monomial, while a polynomial with two terms is a binomial. A polynomial with three terms is a trinomial. Recognizing the type of polynomial can help you understand its structure better.
3. Look for special patterns
Some polynomials have special patterns that can make their classification easier. For example, a polynomial with all terms of the same degree is called a homogeneous polynomial. Identifying these patterns can simplify the process of classification.
4. Use the coefficient of the highest degree term
The coefficient of the highest degree term in a polynomial is also essential in classifying it. For example, if the highest degree term has a positive coefficient, the polynomial is considered to have a positive leading coefficient.
5. Simplify the polynomial
Simplifying the polynomial can also aid in its classification. Combine like terms and reorder the terms to make it easier to identify the type of polynomial.
By following these tips, you can efficiently classify and simplify polynomials, which will be helpful in solving algebraic equations and understanding higher-level mathematical concepts.
Step-by-Step Guide to Simplifying Polynomials
Simplifying polynomials is an important skill in algebra that involves combining like terms and simplifying expressions to make them easier to work with. This step-by-step guide will help you understand how to simplify polynomials effectively.
Step 1: Identify Like Terms
The first step in simplifying polynomials is to identify like terms. Like terms are terms that have the same variables raised to the same powers. For example, 3x and 5x are like terms because they both have the variable x raised to the power of 1. Similarly, 2x^2 and 4x^2 are like terms because they both have the variable x raised to the power of 2.
Make a list of all the like terms in the polynomial expression.
Step 2: Combine Like Terms
Once you have identified the like terms, the next step is to combine them. To combine like terms, simply add or subtract the coefficients of the like terms while keeping the variable and its power the same.
For example, if you have the expression 3x + 5x, you can combine the like terms by adding the coefficients: 3x + 5x = 8x.
Continue combining all the like terms in the expression.
Step 3: Simplify the Expression
After combining all the like terms, simplify the expression further if possible. This may involve performing any necessary arithmetic operations or simplifying any constants.
For example, if you have the expression 2x^2 + 4x^2, you can simplify it by adding the coefficients: 2x^2 + 4x^2 = 6x^2.
If there are no further simplifications possible, then the polynomial is simplified as far as possible.
By following these steps, you will be able to simplify polynomials efficiently and accurately. Practicing these steps with various polynomial expressions will help you master this skill and further enhance your algebraic abilities.
Common Mistakes to Avoid
When classifying and simplifying polynomials, there are a few common mistakes that students often make. By being aware of these mistakes, you can avoid them and improve your understanding and accuracy in working with polynomials.
1. Forgetting to Combine Like Terms
One of the most common mistakes is forgetting to combine like terms when simplifying polynomials. This can result in incorrect answers and can make the process more complicated than it needs to be. Always make sure to carefully combine like terms before simplifying further.
2. Reversing the Order of Operations

Another mistake is reversing the order of operations when simplifying polynomials. The order of operations states that you should simplify expressions inside parentheses first, then perform any multiplication or division, and finally perform any addition or subtraction. Reversing this order can lead to incorrect results.
3. Not Paying Attention to Negative Signs
Many students also make the mistake of not paying attention to negative signs when simplifying polynomials. It’s important to carefully distribute negative signs and perform the necessary operations to simplify expressions correctly. Ignoring or mishandling negative signs can lead to incorrect answers.
4. Incorrectly Classifying Polynomials
Lastly, students often make mistakes when classifying polynomials. It’s important to understand the definitions and characteristics of different types of polynomials, such as quadratic, cubic, or binomial polynomials. Incorrectly classifying a polynomial can lead to errors in further calculations and analysis.
By being aware of these common mistakes and practicing diligently, you can improve your skills in classifying and simplifying polynomials. Paying attention to details and double-checking your work can help you avoid these mistakes and achieve more accurate and confident results.