Welcome to the Radical Expressions and Equations Unit Test Part 1! This test is designed to assess and evaluate your understanding of radical expressions and equations. In this unit, you have learned about various concepts related to radicals, including simplifying radicals, performing operations with radicals, and solving radical equations.
Radicals, also known as square roots, are mathematical expressions that involve taking the square root of a number. They are represented by the radical symbol (√) and can have various degrees, such as square roots (√), cube roots (∛), and so on. Understanding how to manipulate and simplify radicals is essential in algebraic expressions and equations.
During this test, you will be asked to simplify radical expressions, perform operations with radicals, and solve radical equations. You will need to demonstrate your ability to simplify radicals by finding perfect square factors, rationalizing denominators, and applying the multiplication property of radicals. You will also be required to solve radical equations by isolating the radical term and applying appropriate mathematical operations.
Remember to carefully read each question and follow the instructions given. Show all your work and provide clear explanations for your answers. Take your time, double-check your calculations, and don’t hesitate to ask for help if needed. Good luck with the test!
Understanding Radical Expressions and Equations
In the study of mathematics, radical expressions and equations are essential topics that require a solid understanding. A radical expression is an algebraic expression that includes a radical symbol (√) and an expression inside it. This radical symbol represents the operation of taking the square root (or nth root) of a number.
When working with radical expressions, it is important to understand how to simplify them. Simplifying radical expressions involves finding perfect square factors, multiplying and dividing radicals, and rationalizing denominators. This simplification process allows for easier manipulation of the expressions and solving of equations.
Radical equations, on the other hand, are equations that involve radicals. Solving radical equations requires isolating the radical term and then squaring both sides of the equation to eliminate the radical. However, it is important to note that squaring both sides of an equation can introduce extraneous solutions, which are solutions that do not satisfy the original equation.
One common type of radical equation is the quadratic equation, which is a second-degree polynomial equation. Quadratic equations can be solved by factoring, completing the square, or using the quadratic formula. Understanding how to solve these types of equations is crucial for tackling more complex problems in algebra and beyond.
In conclusion, understanding radical expressions and equations is vital for success in mathematics. Mastering the simplification of radical expressions and the solving of radical equations allows for a deeper understanding of algebraic concepts and opens the door to more advanced topics in mathematics.
The Basics of Radical Expressions
In mathematics, a radical expression is an algebraic expression that includes a radical symbol (√). The radical symbol represents a square root or higher order roots such as cube roots or fourth roots. Radical expressions are commonly used to represent numbers that cannot be expressed as simple fractions or decimals.
Radical Notation:
Radical expressions are typically written in the form √a, where “a” is the radicand. The radicand can be any non-negative real number or variable. For example, the expression √9 represents the square root of 9, which is equal to 3. Similarly, √x represents the square root of the variable “x”.
Simplifying Radical Expressions:
One of the main tasks when working with radical expressions is simplifying them. Simplifying radical expressions involves finding the smallest possible expression that represents the same value. This is done by factoring the radicand and simplifying the factors that have perfect square roots.
Operations with Radical Expressions:
In addition to simplifying, operations such as addition, subtraction, multiplication, and division can also be performed with radical expressions. When adding or subtracting radical expressions, the terms with the same radicand can be combined. When multiplying or dividing radical expressions, the same rules of multiplication and division apply, but additional steps may be necessary to simplify the result.
Overall, understanding the basics of radical expressions is essential for solving equations involving radicals and working with more complex mathematical concepts. By mastering the principles, simplifying, and performing operations with radical expressions, students can confidently navigate the realm of radical mathematics.
Simplifying Radical Expressions

When dealing with radical expressions, it is important to simplify them in order to make calculations easier. Simplifying radical expressions involves simplifying the expression under the radical sign, also known as the radicand, and simplifying the expression itself.
To simplify the radicand, you want to find any perfect square factors. For example, if the radicand is 36, you can simplify it by factoring it as 6*6, since 6 is a perfect square. Then, you can write the radical expression as the square root of 6 squared, which simplifies to just 6.
In addition to simplifying the radicand, you also want to simplify the expression itself. This involves combining like terms and performing any necessary operations. For example, if you have the expression √9 + √16, you can simplify it to 3 + 4, which equals 7.
It is important to note that when simplifying radical expressions, you should always look for perfect square factors first. If there are no perfect square factors in the radicand, the expression is already simplified as much as possible. Additionally, remember to use the properties of radicals, such as the product and quotient properties, to simplify the expression further.
In conclusion, simplifying radical expressions involves simplifying the radicand by finding perfect square factors and simplifying the expression itself by combining like terms and performing operations. By simplifying radical expressions, you can make calculations easier and work with more manageable expressions.
Operations with Radical Expressions
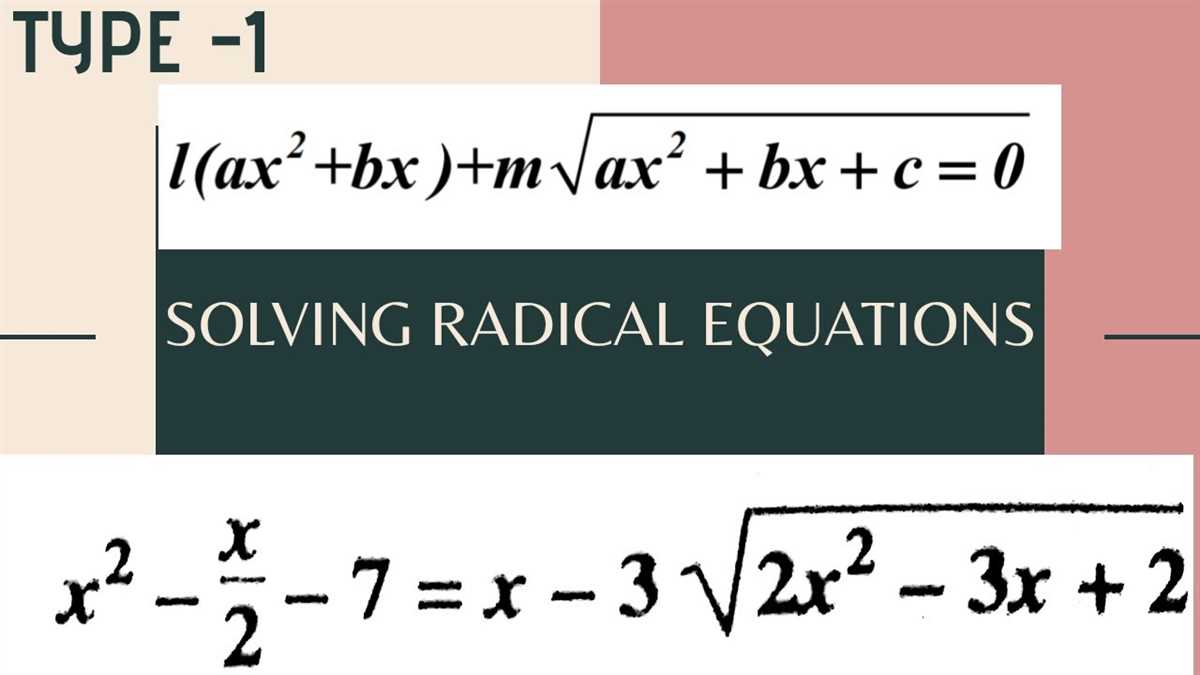
Radical expressions, which include square roots, cube roots, and other radicals, can be manipulated using various operations to simplify and solve equations. These operations include addition, subtraction, multiplication, and division.
When adding or subtracting radical expressions, it is important to simplify them first by combining like terms. Like terms are radical expressions with the same index and radicand. For example, sqrt(3) and 2sqrt(3) are like terms because they have the same radicand, sqrt(3). To add or subtract these terms, simply combine their coefficients. For example, sqrt(3) + 2sqrt(3) = 3sqrt(3).
Multiplication of radical expressions involves multiplying their coefficients and multiplying their radicands. For example, 2sqrt(3) * 3sqrt(3) = 6 * sqrt(3) * sqrt(3) = 6 * sqrt(9) = 6 * 3 = 18. It is important to note that when multiplying radicals with different indices, their indices must be multiplied together.
Division of radical expressions can be done by rationalizing the denominator. This involves multiplying both the numerator and denominator by the conjugate of the denominator. The conjugate of a radical expression is obtained by changing the sign of the radical. For example, to rationalize the denominator of sqrt(5)/sqrt(2), we multiply both the numerator and denominator by sqrt(2), resulting in sqrt(5) * sqrt(2)/(sqrt(2) * sqrt(2)) = sqrt(10)/2.
By understanding and applying these operations, we can simplify radical expressions, combine like terms, and solve equations involving radical expressions with ease and accuracy.
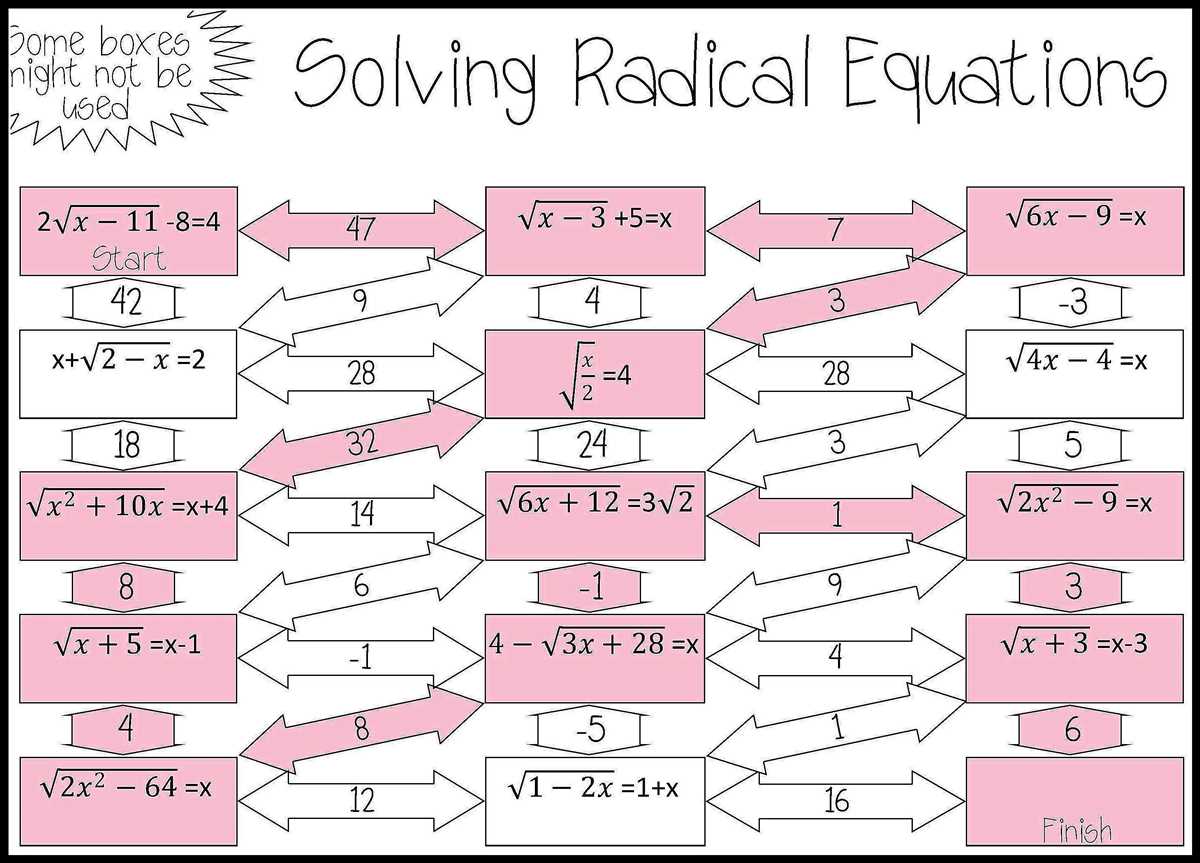
Solving Radical Equations
Solving radical equations involves finding the value or values of the variable that make the equation true. Radical equations are equations that include radicals, which are mathematical expressions that involve a square root or other root operations.
One common type of radical equation is one that includes a square root. To solve these types of equations, you typically need to isolate the radical on one side of the equation and then square both sides to eliminate the radical. It is important to remember that when you square both sides of an equation, you may introduce extraneous solutions, which are solutions that do not satisfy the original equation.
When solving radical equations, it is also important to check your solutions because there might be restrictions on the domain of the variable. For example, if the variable appears in the denominator of a fraction under the radical, that would create an undefined value. Therefore, it is crucial to verify that your solutions are valid and do not violate any domain restrictions.
In summary, solving radical equations involves isolating the radical, squaring both sides to eliminate the radical, and checking the solutions for validity. It is important to be cautious of extraneous solutions and to consider any domain restrictions that may apply to the variable. With practice and understanding of the properties of radicals, you can successfully solve radical equations.
Applying Radical Expressions and Equations
In this article, we have covered various concepts related to radical expressions and equations. We have learned how to simplify radical expressions, solve radical equations, and apply these concepts in real-life situations. Here are the key takeaways from this unit:
Simplifying Radical Expressions

- Radical expressions involve square roots or higher-order roots.
- To simplify a radical expression, we try to simplify the root and the radicand.
- We can simplify the root by factoring the radicand.
- To simplify the radicand, we look for perfect square factors.
- We can combine like terms and perform operations, such as addition, subtraction, multiplication, and division, on radical expressions.
Solving Radical Equations

- Radical equations involve variables inside radicals.
- To solve a radical equation, we try to isolate the radical expression and then square both sides of the equation to eliminate the radical.
- We must check for extraneous solutions, which are solutions that do not satisfy the original equation.
Applications of Radical Expressions and Equations
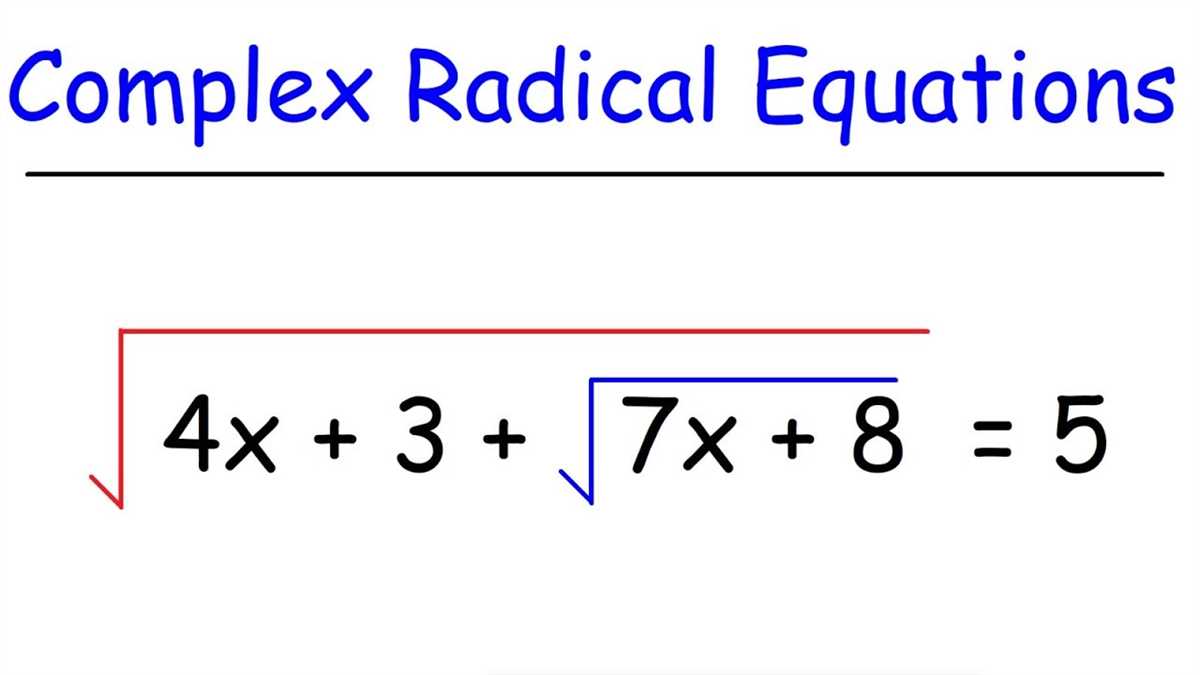
Radical expressions and equations have various applications in real-life situations, such as:
- Calculating distances, areas, and volumes
- Solving problems related to physics, engineering, and finance
- Modeling and analyzing exponential growth and decay
Overall, understanding and applying radical expressions and equations can help us solve complex problems and make meaningful connections between mathematical concepts and real-world scenarios.