Trigonometry, the branch of mathematics that deals with the relationships between the sides and angles of triangles, is a fundamental topic for students studying mathematics. It is often used to solve a variety of problems, including those involving right triangles. Right triangles have one angle measuring 90 degrees, making them particularly interesting and useful in trigonometry.
One popular activity for students studying right triangle trigonometry is the puzzle where they are given a right triangle with some of the sides and angles labeled, and they are asked to find the missing side lengths or angles. This puzzle not only tests their understanding of trigonometric concepts, but also their problem-solving skills.
Once students have completed the puzzle, they may wonder if their answers are correct. This is where the answer key comes in handy. The answer key provides the correct solutions to the puzzle, allowing students to verify their own answers and learn from any mistakes they may have made. It is an essential tool for both students and teachers in the learning process.
Understanding Right Triangle Trigonometry Puzzle Answer Key
Right triangle trigonometry is an essential topic in geometry and mathematics. It involves understanding the relationships between the angles and sides of a right triangle. Trigonometry can be challenging, and one way to reinforce learning is through puzzles and problem-solving activities.
When working on a right triangle trigonometry puzzle, having an answer key is crucial. The answer key provides the solutions to the problems and helps students verify their answers and check for any mistakes. It serves as a guide to understanding the correct approach and methodology for solving the given trigonometric equations.
The right triangle trigonometry puzzle answer key often includes:
- The values of the missing sides or angles
- The step-by-step solutions to the trigonometric equations
- Graphical representations or diagrams to illustrate the solutions
With the answer key, students can compare their solutions and outcomes with the correct answers. This allows them to identify any errors and misconceptions in their approach. It also provides an opportunity for students to learn from their mistakes and enhance their problem-solving skills.
Moreover, the answer key can be a valuable resource for teachers. It helps them evaluate the students’ understanding of right triangle trigonometry and identify areas that need further clarification or reinforcement. It also enables teachers to assess students’ problem-solving abilities and provide targeted feedback for improvement.
In summary, the right triangle trigonometry puzzle answer key plays a significant role in enhancing students’ learning and understanding of trigonometric concepts. It serves as a helpful tool for both students and teachers in ensuring accuracy, identifying errors, and promoting overall mastery of the topic.
Exploring Right Triangle Trigonometry Concepts
Right triangle trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of a right triangle. It is an essential concept in geometry and has numerous applications in various fields of science and engineering. By understanding the fundamental principles of right triangle trigonometry, we can solve complex problems involving angles, distances, and heights.
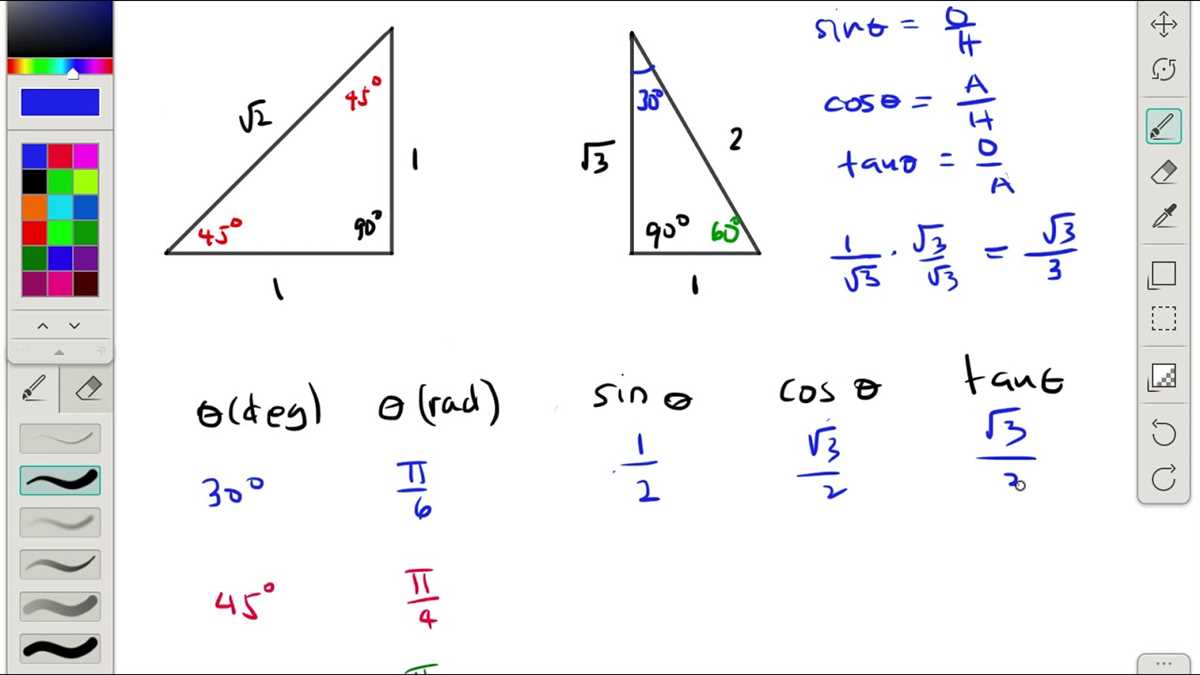
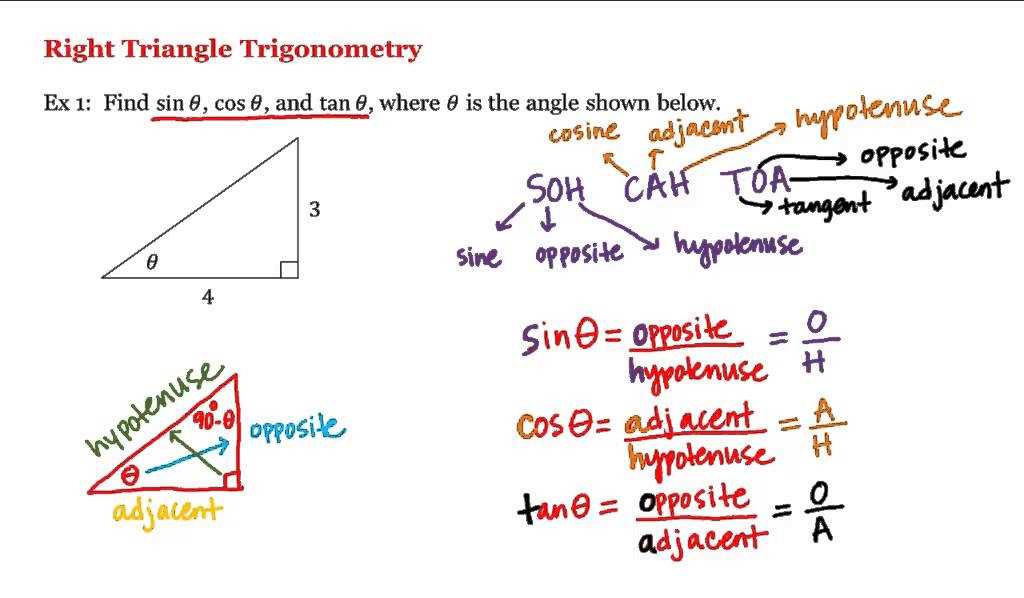
One of the key concepts in right triangle trigonometry is the trigonometric ratios, which relate the angles of a right triangle to its sides. The three primary trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). These ratios are defined as the ratio of the lengths of the sides of a right triangle. For example, the sine of an angle is equal to the ratio of the length of the side opposite the angle to the length of the hypotenuse.
Another important concept in right triangle trigonometry is the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem is often used to find the length of a missing side of a right triangle or to determine if a triangle is a right triangle.
Overall, exploring right triangle trigonometry concepts allows us to solve various real-world problems involving angles and distances. By applying the trigonometric ratios and the Pythagorean theorem, we can calculate heights, distances, and other unknown quantities in a right triangle. This knowledge is valuable in fields such as engineering, physics, and architecture, where accurate measurements and calculations are necessary for successful designs and constructions.
Solving Right Triangle Trigonometry Puzzles Step by Step
Right triangle trigonometry puzzles can be challenging to solve, but by following a step-by-step approach, you can find the answers with ease. These puzzles often involve finding missing angles or side lengths in a right triangle using trigonometric ratios such as sine, cosine, and tangent.
Step 1: Identify the given information. Start by carefully reading the problem and identifying what information is provided. This may include measurements of angles or side lengths in the triangle.
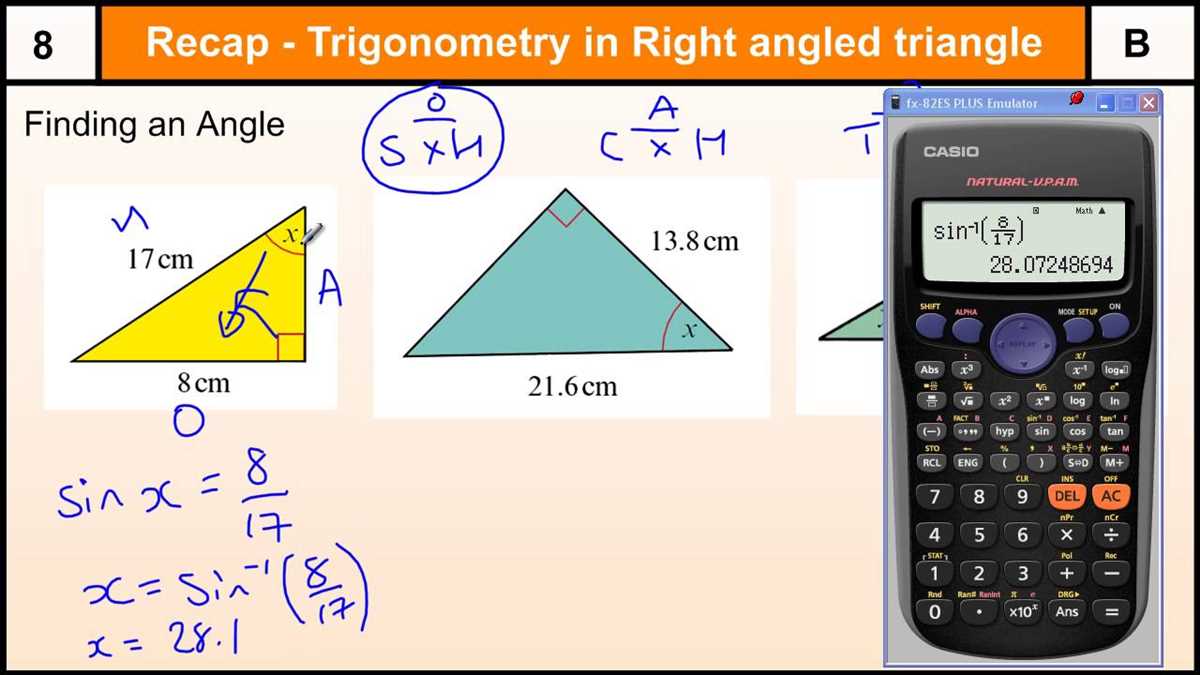
Step 2: Determine which trigonometric ratio to use. Look for clues in the problem that will help you decide which trigonometric ratio to use. For example, if you know the length of the opposite side and the hypotenuse, you can use the sine ratio to find the angle.
Step 3: Set up the trigonometric equation. Using the chosen trigonometric ratio, set up the equation to solve for the unknown variable. Remember to use the appropriate ratio based on the given information.
Step 4: Simplify and solve the equation. Simplify the equation by canceling out any common factors and then solve for the unknown variable. This may involve using inverse trigonometric functions or basic algebraic operations.
Step 5: Check your solution. Once you have found a solution, double-check your work to ensure it makes sense in the context of the problem. Check for any errors in calculations or assumptions made during the solving process.
By following these steps, you can systematically approach right triangle trigonometry puzzles and find the correct solutions. Practice these steps with different puzzles to improve your problem-solving skills and deepen your understanding of trigonometry.
Common Challenges in Right Triangle Trigonometry Puzzles
Right triangle trigonometry puzzles can be challenging, especially for students who are new to the concept. These puzzles often require the use of trigonometric ratios such as sine, cosine, and tangent to solve for missing sides or angles of right triangles. While these puzzles can help students reinforce their understanding of trigonometry, they can also present some common challenges.
One common challenge in right triangle trigonometry puzzles is identifying the appropriate trigonometric ratio to use. Students need to be able to recognize which ratio is needed based on the given information and the unknown they are trying to find. For example, if they are looking to find the length of a side, they may need to use the sine or cosine ratio, while if they are trying to find an angle, they may need to use the inverse of these ratios.
Another challenge is understanding the concept of solving for angles using inverse trigonometric functions. Students may struggle with knowing when to use the inverse sine, cosine, or tangent functions, and how to apply them correctly. This can be especially difficult when angles are given in radians instead of degrees.
Additionally, right triangle trigonometry puzzles often involve multiple steps and require students to use multiple trigonometric ratios. This can be overwhelming for some students, as they need to carefully combine the ratios to solve for the unknown variables. It is important for students to be able to break down the problem into smaller steps and use the appropriate trigonometric ratios at each step.
In conclusion, right triangle trigonometry puzzles can present various challenges for students. It is important for students to have a strong understanding of trigonometric ratios and inverse trigonometric functions, as well as the ability to break down problems into smaller steps. Practice and familiarity with these types of puzzles can help students improve their skills in right triangle trigonometry.
Key Tips and Strategies for Mastering Right Triangle Trigonometry
Right triangle trigonometry can be challenging, but with the right tips and strategies, you can master it! Here are some key suggestions to help you become proficient in this important branch of mathematics:
- Understand the basics: Before diving into complex problems, make sure you have a solid understanding of the basic concepts and formulas of right triangle trigonometry. Familiarize yourself with the sine, cosine, and tangent ratios, as well as the Pythagorean theorem.
- Practice with real-life examples: Applying right triangle trigonometry to real-life scenarios can help you understand its practical applications and increase your problem-solving skills. Look for opportunities to use trigonometry in everyday situations, such as measuring distances or angles.
- Draw diagrams: Visual representations can greatly aid your understanding of right triangle trigonometry. When solving a problem, draw a clear diagram that accurately represents the given information. This will help you visualize the relationships between the angles and sides of the triangle.
- Memorize the special right triangles: Memorizing the ratios for the special 30-60-90 and 45-45-90 right triangles can save you time in calculations. These triangles have consistent ratios that make solving certain problems quicker and easier.
- Practice using trigonometric identities: Trigonometric identities, such as the reciprocal, quotient, and Pythagorean identities, can simplify complex expressions and equations. Make sure to practice using these identities to enhance your problem-solving skills.
- Work on a variety of problems: To truly master right triangle trigonometry, practice solving a wide range of problems. Start with simple exercises and gradually move on to more challenging ones. The more exposure you have to different types of problems, the more confident you will become in your abilities.
- Seek help when needed: If you’re stuck on a concept or problem, don’t hesitate to seek help. Reach out to your teacher, classmates, or online resources for clarification. Sometimes a fresh perspective or explanation can make all the difference in your understanding.
By following these key tips and strategies, you’ll be well on your way to mastering right triangle trigonometry. Remember, practice and perseverance are key to becoming proficient in any subject. Keep practicing, stay persistent, and you’ll soon become a trigonometry whiz!
Q&A:
What is right triangle trigonometry?
Right triangle trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of a right triangle.
How do you find the missing side of a right triangle using trigonometry?
To find the missing side of a right triangle using trigonometry, you can use either the sine, cosine, or tangent functions. These functions relate the angles of the triangle to the lengths of the sides.
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
What are some key tips for mastering right triangle trigonometry?
Some key tips for mastering right triangle trigonometry are: understanding the definitions of sine, cosine, and tangent; memorizing the special right triangles; practicing solving problems involving right triangles; and familiarizing yourself with the various trigonometric identities and their applications.
What are some common applications of right triangle trigonometry?
Right triangle trigonometry is used in a variety of fields and applications, including engineering, architecture, physics, navigation, and computer graphics. It is used to solve problems involving angles, distances, heights, and more.
What are the key principles of right triangle trigonometry?
The key principles of right triangle trigonometry include the relationships between the lengths of the sides and the measures of the angles in a right triangle. These principles are based on the trigonometric functions sine, cosine, and tangent.
What are some strategies for mastering right triangle trigonometry?
Some strategies for mastering right triangle trigonometry include practicing with different types of right triangles, memorizing the definitions and formulas of the trigonometric functions, and understanding how to apply them in real-life situations. It is also helpful to work through sample problems and seek additional resources or guidance if needed.