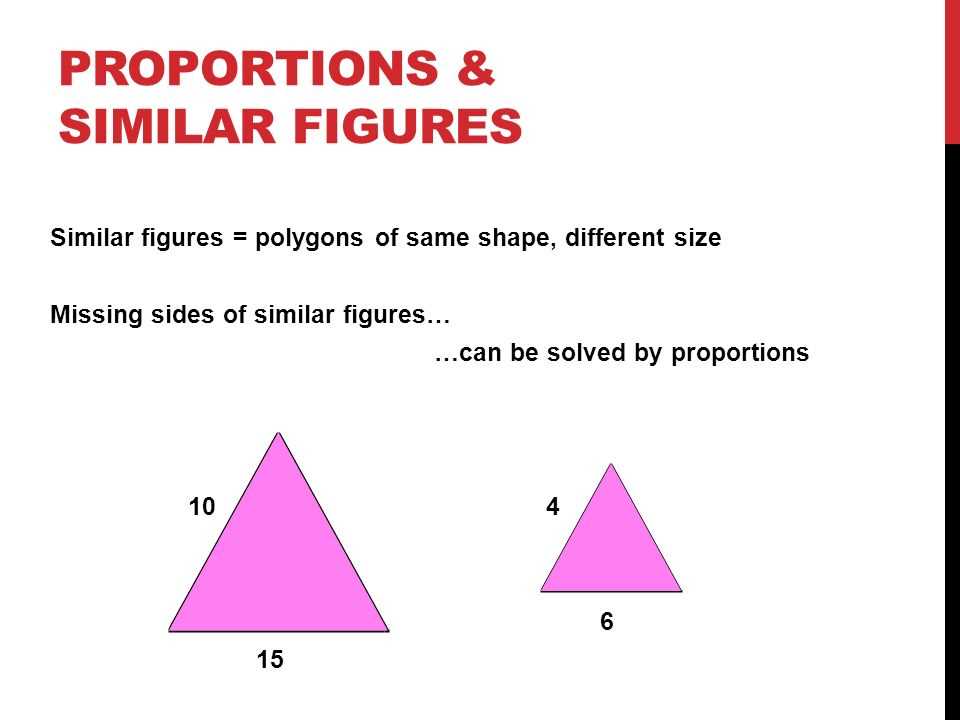
In geometry, one of the important concepts students learn is the idea of similar figures. Similar figures are figures that have the same shape, but not necessarily the same size. Understanding similarity is crucial for various geometric applications, such as scale drawings, proportional reasoning, and trigonometry. To assess students’ knowledge and understanding of similar figures, teachers often administer test reviews.
A similar figures test review typically includes a variety of questions that challenge students to apply their understanding of similarity. These questions may involve comparing ratios, solving proportions, determining corresponding angles, or finding missing side lengths. By practicing similar figures test review questions, students enhance their ability to identify and analyze similar figures in different contexts.
One key strategy for approaching similar figures test review is to first identify the properties and characteristics of similar figures. Students should be familiar with the definition of similarity, which states that corresponding angles are congruent and corresponding side lengths are proportional. Additionally, they should understand the concept of scale factor, which is the ratio of corresponding side lengths in similar figures.
What Are Similar Figures?
When two figures are similar, their corresponding sides are in proportion. This means that the ratios of the lengths of the corresponding sides are equal. For example, if one side of a triangle is twice as long as the corresponding side of another triangle, then the other sides will also be in this same ratio of 1:2.
Similar figures can be found in many real-life situations. For example, maps use similar figures to represent actual locations on a smaller scale. Architectural blueprints also use similar figures to represent buildings. Understanding similar figures is important in geometry because it allows us to analyze and compare shapes and understand how they relate to each other.
Properties of Similar Figures:
- Corresponding angles are congruent
- Corresponding sides are proportional
- Perimeters are in proportion
- Areas are in proportion (squared ratio)
Similar figures provide us with a useful tool for solving problems in geometry. By identifying the corresponding parts of similar figures and using their proportions, we can find missing side lengths and angles, calculate areas, and solve various geometric problems.
Properties of Similar Figures
Similar figures are figures that have the same shape but may have different sizes. They can be compared to each other by examining their corresponding sides and angles. There are several properties that can help identify and work with similar figures.
Corresponding Angles: Similar figures have corresponding angles that are equal in measure. This means that if two angles in one figure are equal, their corresponding angles in the other figure will also be equal. By identifying and comparing corresponding angles, we can determine if two figures are similar.
Corresponding Sides: Similar figures also have corresponding sides that are proportional in length. This means that the ratio of the lengths of corresponding sides in one figure will be equal to the ratio of the lengths of their corresponding sides in the other figure. By comparing the ratios of corresponding side lengths, we can determine if two figures are similar.
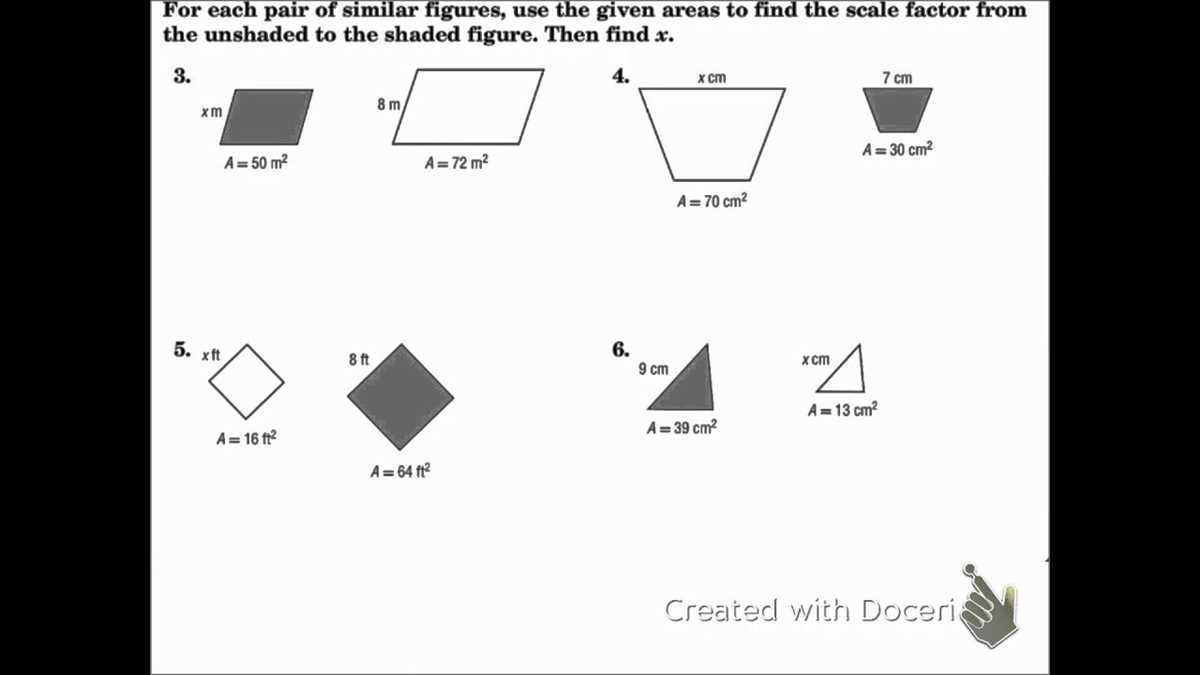
Scale Factor: The scale factor is the ratio of the lengths of corresponding sides in similar figures. It can be used to find missing side lengths or determine the size relationship between two similar figures. The scale factor is calculated by dividing the length of one corresponding side in one figure by the length of the corresponding side in the other figure.
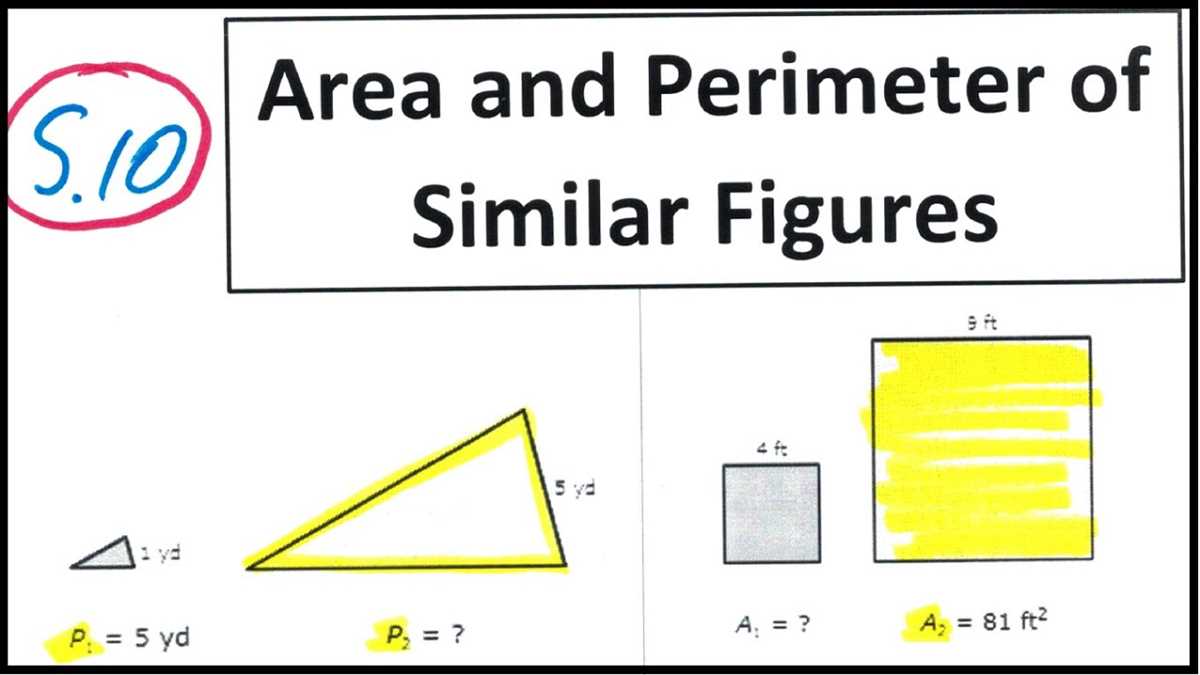
Proportional Perimeters and Areas: If two figures are similar, their perimeters and areas will also be proportional. The ratio of the perimeters of two similar figures is equal to the ratio of their corresponding side lengths, while the ratio of their areas is equal to the square of the ratio of their corresponding side lengths.
Triangle Similarity: In triangles, there are different criteria for determining similarity. The Side-Angle-Side (SAS) criterion states that if two sides of one triangle are proportional to two corresponding sides of another triangle and the included angles are congruent, then the triangles are similar. The Angle-Angle (AA) criterion states that if two angles of one triangle are congruent to two corresponding angles of another triangle, then the triangles are similar.
How to Determine if Two Figures are Similar
When dealing with the topic of similar figures, it is important to know how to determine if two figures are indeed similar. There are several key concepts and techniques that can be used to make this determination.
One of the first things to look for when comparing two figures is the ratio of their corresponding sides. If the ratios of the corresponding sides are equal, then the figures are likely similar. This can be done by comparing the lengths of the corresponding sides and calculating their ratios.
Additionally, it is important to check if the corresponding angles of the figures are equal. If the angles are equal, this is another indication that the figures are similar. To determine if the angles are equal, you can measure or calculate the angles and compare them.
Another technique that can be used to determine similarity is the use of transformations. If two figures can be mapped onto each other using transformations such as translations, reflections, rotations, or dilations, then they are similar. By applying these transformations to the figures and checking if they align, you can determine if they are similar.
In conclusion, there are multiple methods that can be used to determine if two figures are similar. These include comparing the ratios of corresponding sides, checking for equal corresponding angles, and using transformations to map one figure onto the other. By utilizing these techniques, you can confidently determine if two figures are indeed similar.
Methods for Proving Figures are Similar
When it comes to proving that two figures are similar, there are several methods that can be used. These methods rely on identifying and comparing specific attributes of the figures to determine if they have the same shape, but possibly different sizes.
One method for proving figures are similar is using the Angle-Angle (AA) criterion. This method involves comparing the angles of two figures. If the corresponding angles of the two figures are congruent, meaning they have the same measure, then the figures are considered to be similar. This method is based on the fact that corresponding angles of similar figures are always congruent.
Another method for proving similarity is using Side-Angle-Side (SAS) criterion. This method involves comparing the sides and angles of two figures. If the corresponding sides of the two figures are proportional and the included angle is congruent, then the figures are considered to be similar. This method relies on the fact that corresponding sides of similar figures are always proportional.
This table summarizes the methods for proving figures are similar:
| Method | Criterion |
|---|---|
| Angle-Angle (AA) | Corresponding angles are congruent |
| Side-Angle-Side (SAS) | Corresponding sides are proportional and included angle is congruent |
By using these methods, mathematicians and students can confidently determine whether or not two figures are similar. This is important in various fields, such as geometry and engineering, where the similarity of figures is a key concept in solving problems and making accurate measurements.
Applications of Similar Figures
Similar figures are a crucial concept in geometry that finds a wide range of applications in various real-life situations. A similar figure refers to a shape that has the same shape but may vary in size and orientation. These figures have proportional sides and angles, allowing us to use their properties to solve complex problems.
Architectural Blueprint: The concept of similar figures is extensively applied in architecture. Architects use scaled drawings to represent the actual size of a building on a smaller piece of paper. By creating a scaled blueprint, architects can accurately represent the dimensions and proportions of a building. Similarly, model makers create small-scale models of buildings using the principles of similar figures to achieve a realistic representation.
Map Navigation: Similar figures are commonly used in map navigation to calculate distances and determine directions. Different scales on maps allow us to estimate the actual distance between two locations. By comparing the lengths of two corresponding sides on a map, we can determine the actual distance by using the concept of similar figures. Moreover, the use of compasses helps to calculate angles and determine the direction of travel.
Other Applications:
- Engineering and construction utilize similar figures to design and build structures such as bridges, towers, and tunnels.
- Photography and cinematography use the concept of similar figures to create special effects and achieve perspective in visual arts.
- Astronomy relies on similar figures to model the scale and proportions of celestial bodies and to understand the vastness of the universe.
In conclusion, the concept of similar figures has significant practical applications in geometry. Its utilization extends to diverse fields and industries, ranging from architecture to map navigation, engineering, and even visual arts and astronomy. Understanding the principles of similar figures enables us to solve complex problems and accurately represent real-life objects and situations.
Practice Test and Solutions
Here is a practice test to help you review your knowledge of similar figures. Use this test to test your understanding of the concepts and see if you are ready for the actual exam.
Below, you will find ten multiple-choice questions. Read each question carefully and select the best answer choice. After you have completed the test, review the solutions to see which choices were correct and why.
Practice Test
- Question 1: Two triangles are similar if:
- a) They have the same shape
- b) They have the same size
- c) Their corresponding angles are congruent
- d) Their corresponding side lengths are proportional
- Question 2: Two rectangles are similar if:
- a) They have the same shape
- b) They have the same size
- c) Their corresponding angles are congruent
- d) Their corresponding side lengths are proportional
- Question 3: Two circles are similar if:
- a) They have the same shape
- b) They have the same size
- c) Their corresponding angles are congruent
- d) Their corresponding radii are proportional
- Question 4: The scale factor between two similar figures is:
- a) The ratio of their corresponding perimeters
- b) The ratio of their corresponding areas
- c) The ratio of their corresponding side lengths
- d) The ratio of their corresponding angles
- Question 5: Two polygons are similar if:
- a) They have the same shape
- b) They have the same size
- c) Their corresponding angles are congruent
- d) Their corresponding side lengths are proportional
- Question 6: If the scale factor between two similar figures is 2:3, what is the ratio of their areas?
- a) 2:3
- b) 4:9
- c) 6:9
- d) 8:9
- Question 7: If two circles are similar, what is the relationship between their radii?
- a) They are congruent
- b) They are proportional
- c) They have the same length
- d) There is no relationship between their radii
- Question 8: If two polygons are similar, what is the relationship between their corresponding angles?
- a) They are congruent
- b) They are proportional
- c) They have the same measure
- d) There is no relationship between their corresponding angles
- Question 9: If two triangles are similar, what is the relationship between their side lengths?
- a) They are congruent
- b) They are proportional
- c) They have the same length
- d) There is no relationship between their side lengths
- Question 10: If two rectangles are similar, what is the relationship between their corresponding side lengths?
- a) They are congruent
- b) They are proportional
- c) They have the same length
- d) There is no relationship between their corresponding side lengths
Solutions
1) c) Their corresponding angles are congruent
2) d) Their corresponding side lengths are proportional
3) d) Their corresponding radii are proportional
4) c) The ratio of their corresponding side lengths
5) d) Their corresponding side lengths are proportional
6) b) 4:9
7) b) They are proportional
8) b) They are proportional
9) b) They are proportional
10) b) They are proportional
By reviewing the practice test and solutions, you can assess your understanding of similar figures. Remember to study the concepts and practice solving problems to improve your skills before taking the actual test.