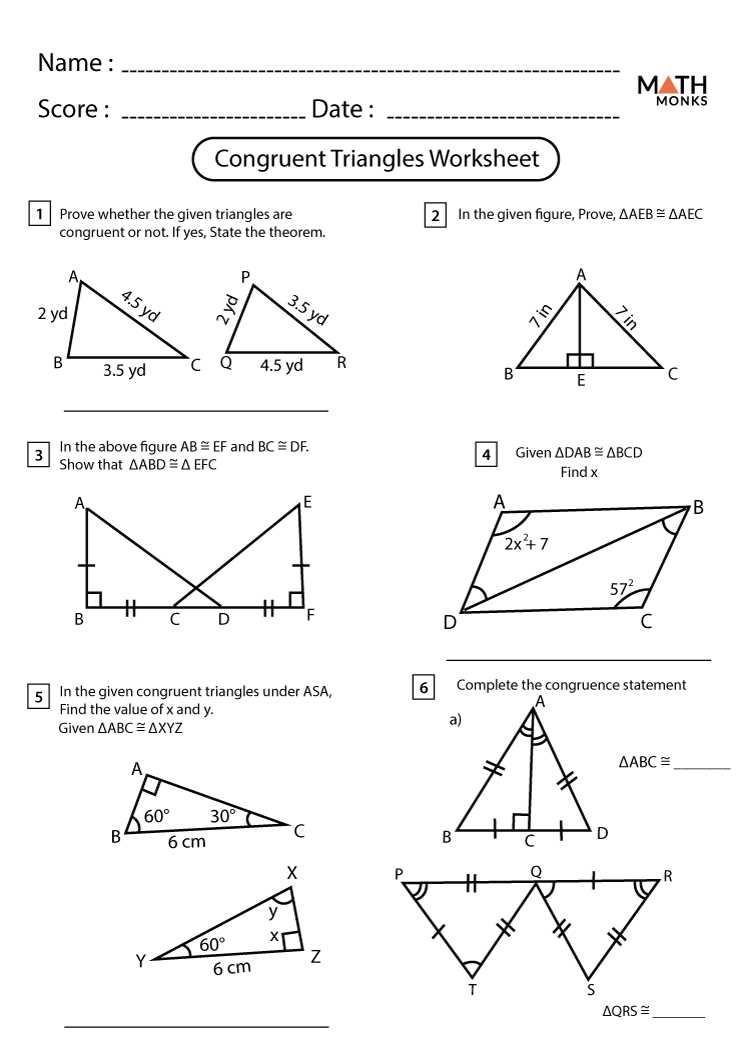
Do you need practice on similar triangles and want to test your knowledge? Look no further! This article provides a helpful worksheet with answers in PDF format that you can easily download and print. Similar triangles are an important concept in geometry and understanding their properties and relationships is crucial in solving various mathematical problems.
The worksheet includes a variety of exercises that cover topics such as identifying similar triangles, finding missing side lengths, and determining unknown angles. Each exercise is accompanied by detailed step-by-step solutions so you can check your work and learn from any mistakes.
Working through this worksheet will not only improve your understanding of similar triangles, but it will also strengthen your problem-solving skills. With the answers provided, you can easily track your progress and identify areas that may require further practice.
Similar Triangles Worksheet PDF with Answers
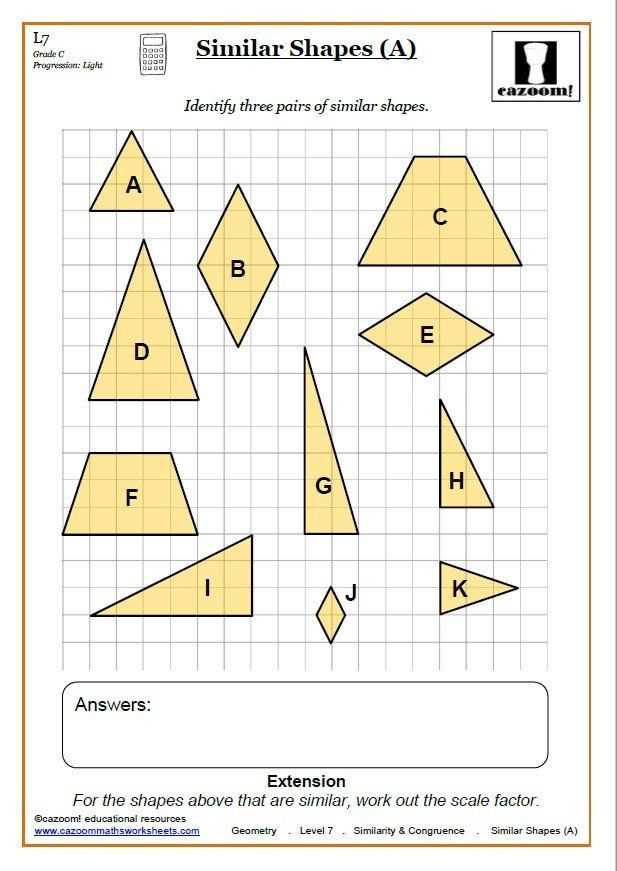
In mathematics, similar triangles are triangles that have the same shape, but may have different sizes. They have the same angles, but their side lengths may be proportional. Determining if two triangles are similar can be a useful tool in solving various geometric problems.
A similar triangles worksheet in PDF format is a great resource for practicing and testing your understanding of this concept. These worksheets usually consist of multiple problems, where you are given two triangles and asked to determine if they are similar. You may also be asked to find missing side lengths or angles in similar triangles.
These worksheets often include clear diagrams to help you visualize the triangles and understand the given information. They provide an opportunity to apply the properties and theorems related to similar triangles, such as the Angle-Angle Similarity Theorem, Side-Side-Side Similarity Theorem, and Side-Angle-Side Similarity Theorem.
With the answers provided in the PDF, you can check your work and make sure you are on the right track. If you get an incorrect answer, you can review the solution and identify any mistakes you made.
Practicing with similar triangles worksheets can improve your problem-solving skills and strengthen your understanding of geometric concepts. They are also a helpful resource for teachers and tutors to assess their students’ knowledge and provide targeted instruction.
Overall, a similar triangles worksheet in PDF format with answers is an excellent tool for practicing and mastering this important geometric concept.
Identifying Similar Triangles
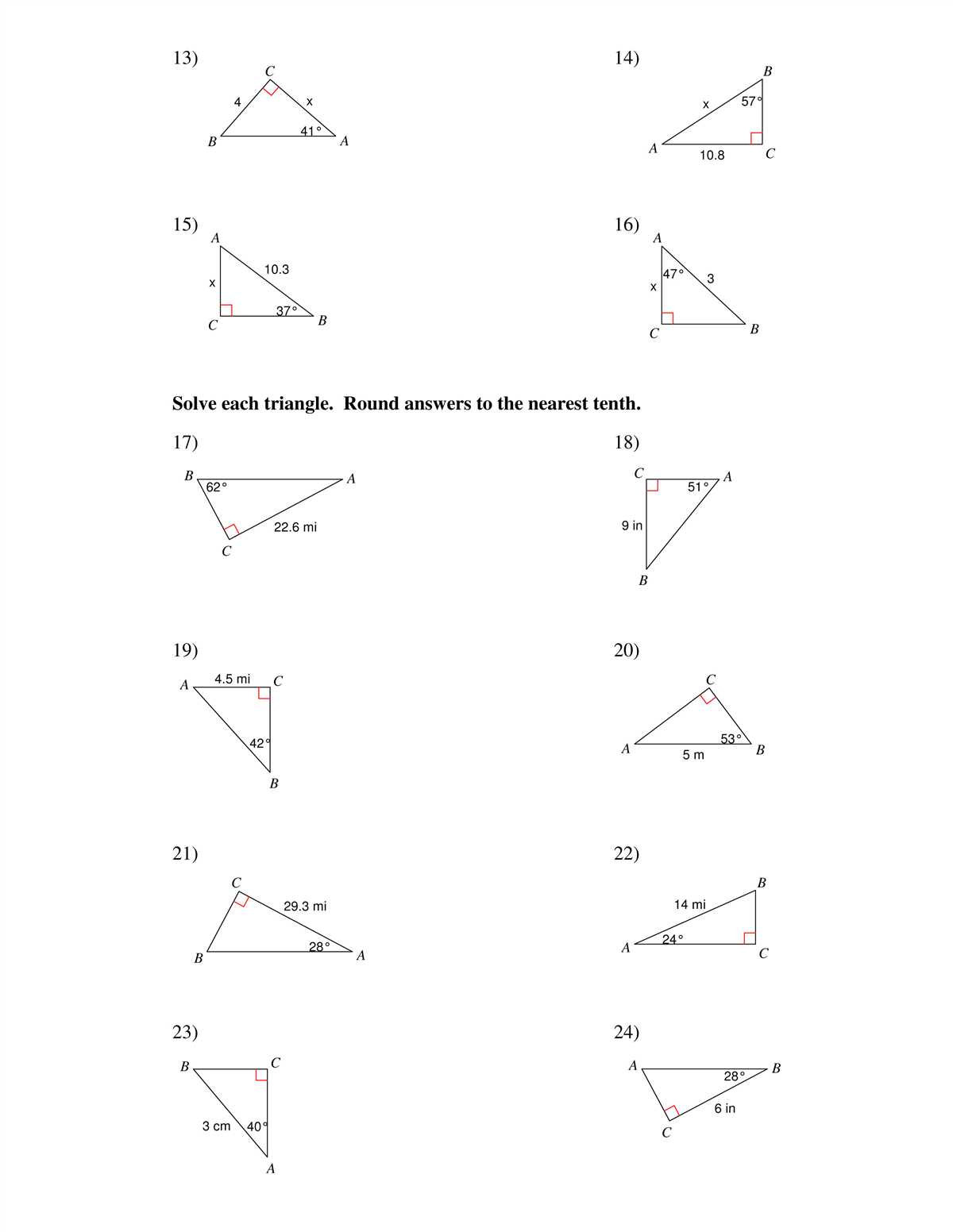
Similar triangles are triangles that have the same shape, but not necessarily the same size. They have corresponding angles that are equal and corresponding sides that are proportional. Identifying similar triangles involves comparing the angles and sides of two triangles to determine if they are similar.
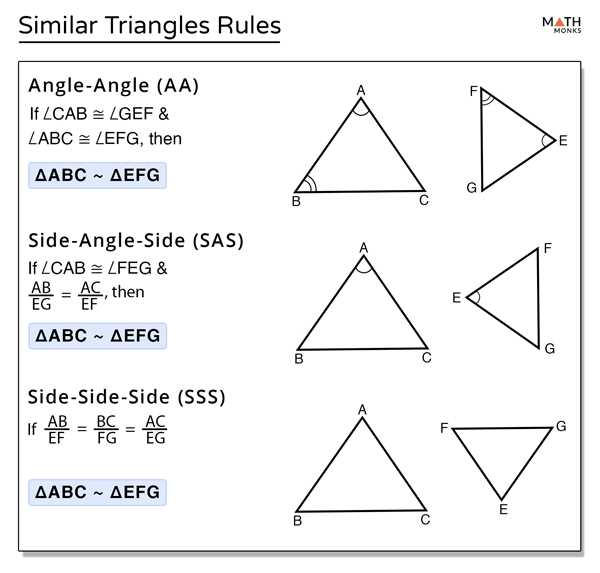
To determine if two triangles are similar, you can use the AA similarity postulate, which states that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. Another way to identify similar triangles is by using the SAS similarity theorem, which states that if two sides of one triangle are proportional to two sides of another triangle and the included angles are congruent, then the triangles are similar.
When identifying similar triangles, it is important to pay attention to the order in which the angles and sides are listed. For example, if triangle ABC is similar to triangle DEF, you would write it as ABC ~ DEF. The corresponding angles and sides must be listed in the same order on both triangles.
By identifying similar triangles, you can solve problems involving proportions, find missing side lengths or angles, and determine if two figures are congruent or not. This concept is important in various fields such as geometry, engineering, and architecture, where knowledge of similar triangles can be applied to solve real-world problems and make accurate calculations.
Proving Triangles are Similar
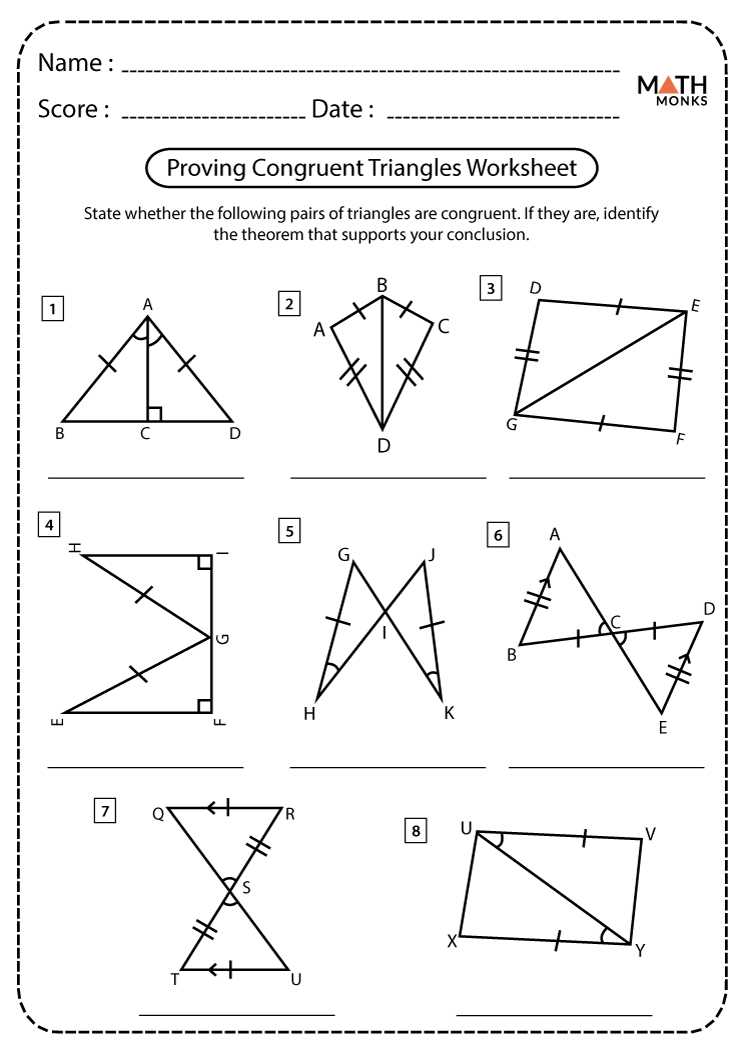
When proving that two triangles are similar, there are several methods that can be used depending on the given information. One common method is the Angle-Angle (AA) similarity theorem, which states that two triangles are similar if they have two corresponding angles that are congruent.
Another method is the Side-Angle-Side (SAS) similarity theorem, which states that two triangles are similar if they have one pair of corresponding sides that are proportional and the included angles are congruent.
To prove that triangles are similar, it is important to show that the corresponding angles or sides are congruent or proportional. This can be done through various techniques such as using angle measures, side lengths, or proportions.
- One method is to use the triangle similarity postulates, such as AA, SAS, or Side-Side-Side (SSS) similarity.
- Another method is to use similar triangle properties, such as corresponding angles, corresponding sides, or altitude similarity.
- For example, if two pairs of corresponding angles are congruent and a pair of corresponding sides are proportional, the triangles can be proven similar using the SAS similarity theorem.
It is important to remember that proving triangles are similar requires careful analysis of the given information and applying the appropriate similarity theorem or property. Additionally, providing a clear and logical explanation is essential to support the proof.
Applying Similar Triangles
Applying similar triangles involves using the properties of similar triangles to solve problems and find missing lengths or angles. Similar triangles have corresponding angles that are congruent, and their corresponding sides are in proportion.
One way to apply similar triangles is to use the principle of corresponding angles. If two triangles have the same angles, then their corresponding sides are proportional. This means that if we know the lengths of some sides of one triangle and the lengths of corresponding sides of the other triangle, we can use proportions to find the lengths of the remaining sides.
Another way to apply similar triangles is to use the principle of the angle-angle similarity postulate. If two triangles have two pairs of corresponding angles that are congruent, then the triangles are similar. This means that we can set up proportions and solve for the missing lengths or angles.
Solving problems involving similar triangles often requires setting up proportions and solving for variables. Sometimes we need to use properties of similar triangles, such as the side-splitter theorem or the triangle proportionality theorem, to find missing lengths or angles.
Overall, applying similar triangles is a powerful tool in geometry that allows us to find missing lengths and angles in triangles. By recognizing the properties of similar triangles and using proportions, we can solve a variety of problems involving similar triangles.
Solving Problems with Similar Triangles
When it comes to solving problems involving similar triangles, there are a few key concepts to keep in mind. First, it is important to understand what it means for two triangles to be similar. Two triangles are considered similar if their corresponding angles are congruent and their corresponding sides are proportional. This proportional relationship is often represented using the symbol ~.
One common problem involves finding missing side lengths or angles in similar triangles. To do this, we can use the concept of proportional sides. If we know the lengths of certain sides in one triangle and the lengths of corresponding sides in the other triangle, we can set up a proportion to find the unknown side length. For example, if the sides of one triangle have lengths of 4, 5, and 6, and the corresponding sides of another triangle have lengths of 8, x, and 12, we can set up the proportion 4/8 = 5/x = 6/12 and solve for x.
Another type of problem involves finding the scale factor between two similar triangles. The scale factor represents the ratio of corresponding side lengths between the two triangles. To find the scale factor, we can divide the length of a side in one triangle by the corresponding side length in the other triangle. For example, if one triangle has side lengths of 4, 6, and 8, and the corresponding side lengths in another triangle are 8, 12, and 16, we can find the scale factor by dividing 4/8, 6/12, and 8/16, which results in a scale factor of 1/2.
Summary

In this article, we have explored the concept of similar triangles and provided a worksheet in PDF format with answers. Similar triangles are triangles that have the same shape but may differ in size. We discussed the criteria for two triangles to be similar, such as having corresponding angles that are equal and corresponding sides that are proportional.
The worksheet we provided offers various exercises to practice identifying similar triangles, finding missing side lengths, and solving for unknown angles. Each exercise is accompanied by a detailed answer key, allowing students to verify their solutions and understand the steps involved in solving each problem.
In addition to the worksheet, we have also discussed the importance of understanding similar triangles in various real-world applications, such as scaling objects, calculating heights and distances, and analyzing geometric relationships. The ability to recognize and work with similar triangles is essential in geometry and lays the foundation for more advanced concepts in mathematics.
By practicing with the provided worksheet and understanding the concepts of similar triangles, students can enhance their problem-solving skills, develop a deeper understanding of geometric relationships, and improve their overall mathematical abilities.
Resources:
- Worksheet: Similar Triangles Worksheet PDF with Answers