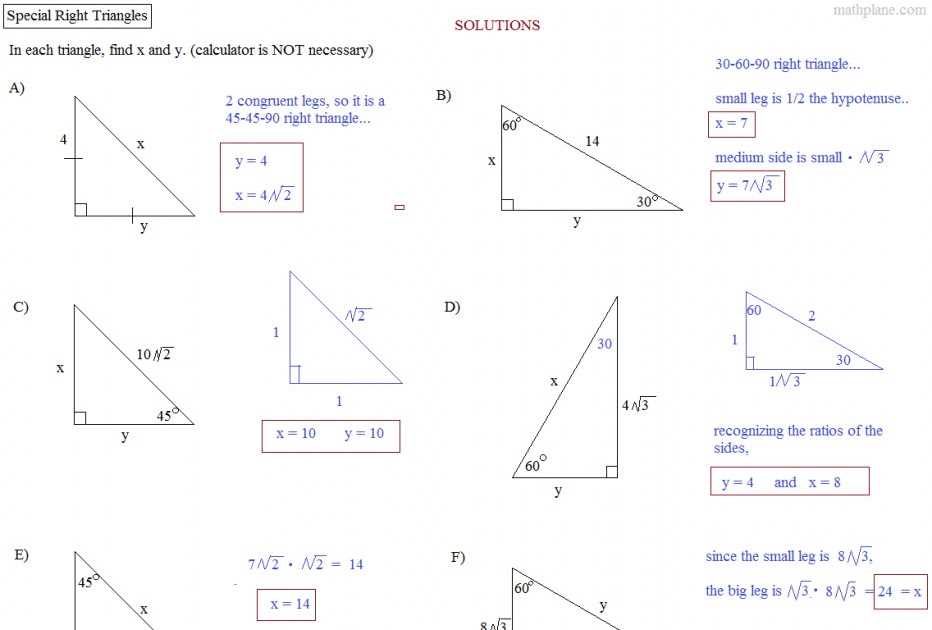
When working with triangles, it is often necessary to find missing side lengths or angles. To do this, we can use various trigonometric formulas and principles. However, it is important to pay attention to the precision of our answers. This article discusses the importance of rounding our answers to the nearest tenth and provides examples of how to solve triangles using this rounding method.
Rounding our answers to the nearest tenth helps to ensure that our calculations are accurate enough for most practical purposes. By rounding to the nearest tenth, we can eliminate unnecessary decimal places and make our answers more manageable and easier to work with. This precision is usually sufficient for everyday applications in fields such as engineering, architecture, and physics.
To solve a triangle using the rounding method, we first need to identify the given information. This usually includes at least one side length and one angle measure. We can then use trigonometric functions such as sine, cosine, and tangent to find the missing side lengths or angles. After performing the necessary calculations, we round our answers to the nearest tenth.
For example, if we are given a triangle with two side lengths and an angle measure, we can use the law of sines or the law of cosines to find the remaining side length and angle measures. Once we have obtained these values, we apply the rounding method by looking at the decimal place of the first digit after the tenth. If it is five or greater, we round up; if it is less than five, we round down. This allows us to obtain a more precise answer that is still easy to interpret and use in practical applications.
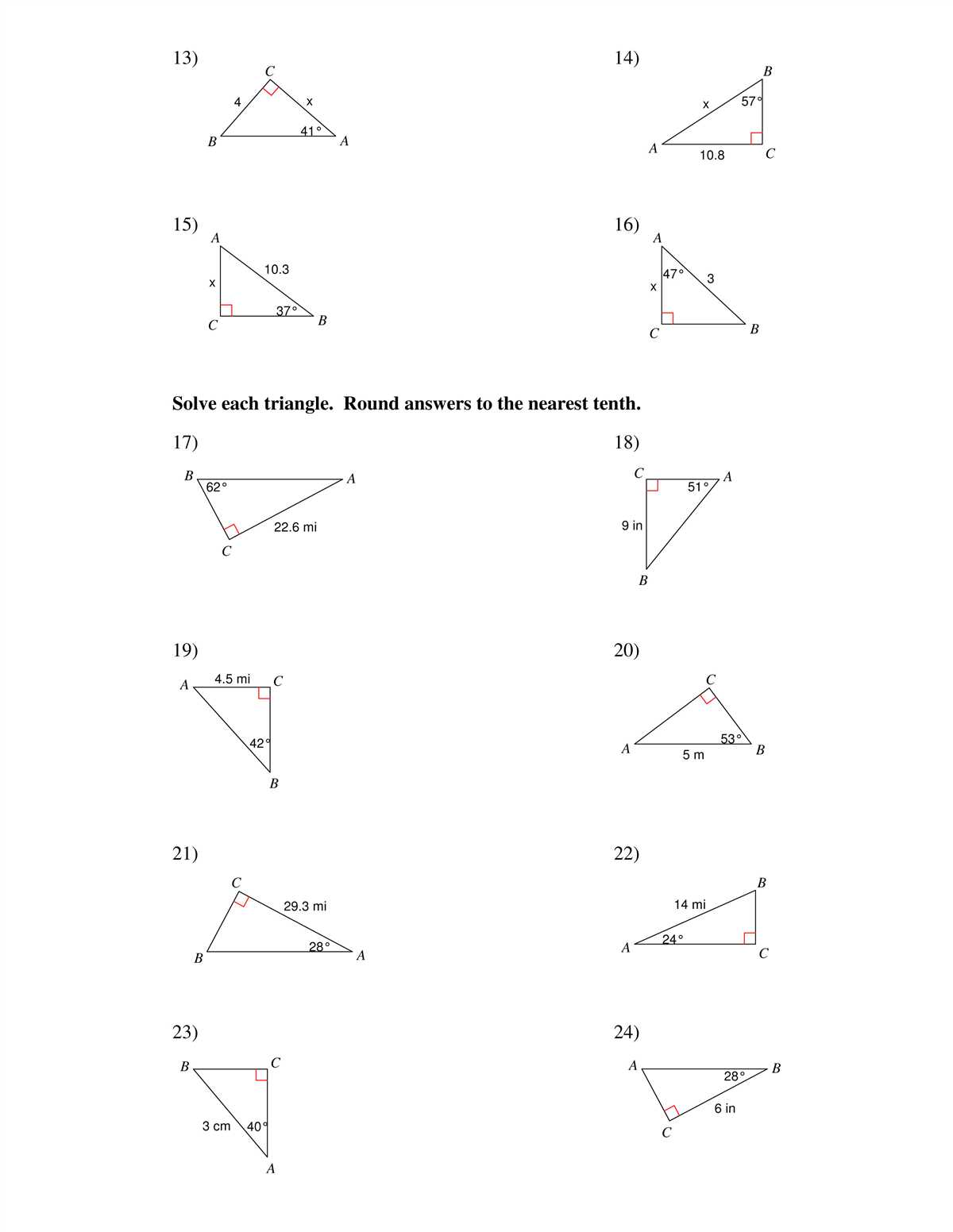
Solve Each Triangle Round Answers to the Nearest Tenth
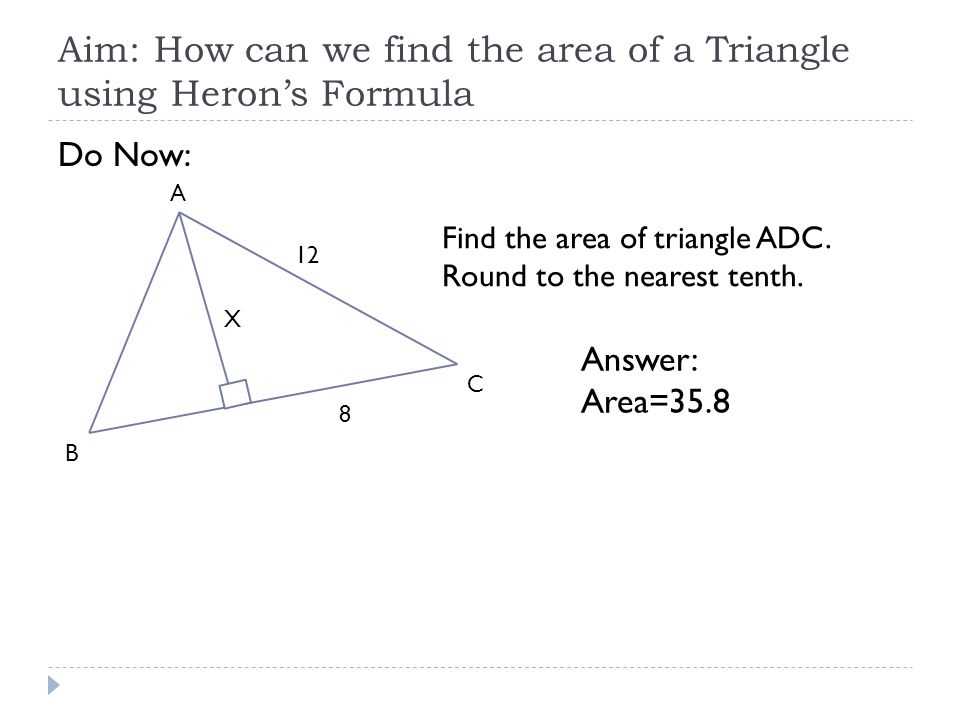
When working with triangles, it is often necessary to find the lengths of the sides and the measures of the angles. However, these values are not always given directly, and it requires solving the triangle using various trigonometric formulas and principles.
In order to solve each triangle, it is important to remember to round the answers to the nearest tenth. This is because the measurements of angles and sides in triangles are typically given with decimal places, and rounding to the nearest tenth ensures that the answers remain accurate but more manageable.
One common method of solving triangles is using the Law of Sines and the Law of Cosines. The Law of Sines relates the ratios of the lengths of the sides to the sines of their opposite angles, while the Law of Cosines relates the lengths of the sides to the cosine of their adjacent angles. By using these formulas, it is possible to find the missing measurements of triangles.
Another approach to solving triangles is by using trigonometric functions such as sine, cosine, and tangent. These functions can be used to find the lengths of sides and the measures of angles in right triangles. By applying these functions to the given information, it is possible to round the answers to the nearest tenth and obtain accurate results.
In summary, when solving each triangle, it is important to round the answers to the nearest tenth. This ensures that the measurements remain accurate while being more manageable. By using trigonometric formulas and principles such as the Law of Sines, the Law of Cosines, and trigonometric functions, it is possible to find the missing measurements of triangles and solve each triangle effectively.
Understanding Triangles and Their Properties
A triangle is a polygon with three sides and three angles. It is one of the most basic and fundamental shapes in geometry. Triangles can vary in size, shape, and angles, giving rise to different classifications and properties.
One key property of triangles is that the sum of the interior angles is always 180 degrees. This is known as the Triangle Angle Sum Theorem. It means that no matter the size or shape of a triangle, the sum of its angles will always add up to 180 degrees. This property is useful in solving triangle problems and determining missing angles.
Triangles can be classified based on their angles. An acute triangle has all angles less than 90 degrees, while a right triangle has one angle equal to 90 degrees. An obtuse triangle has one angle greater than 90 degrees. Additionally, triangles can be classified based on their side lengths. An equilateral triangle has all sides equal in length, while an isosceles triangle has two sides of equal length. A scalene triangle has no sides of equal length.
The properties of triangles are interconnected, allowing for various calculations and relationships to be derived. For example, the Pythagorean Theorem relates the sides of a right triangle, stating that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem is widely used in geometry and has practical applications in fields such as engineering and construction.
Solving Triangles Using Trigonometric Functions
In mathematics, trigonometric functions are often used to solve triangles. These functions involve the relationships between the angles and sides of a triangle. By using the sine, cosine, and tangent functions, we can determine the unknown angles and sides of a triangle.
One of the most common ways to solve a triangle is by using the Law of Sines and the Law of Cosines. The Law of Sines states that the ratio of the length of a side of a triangle to the sine of its opposite angle is constant. The Law of Cosines, on the other hand, relates the lengths of the sides of a triangle to the cosine of one of its angles.
To solve a triangle using trigonometric functions, we typically start by identifying what information is given. This could include the lengths of the sides or the measures of the angles. From there, we can determine which trigonometric function to use based on the known information.
For example, if we know two angles and one side of a triangle, we can use the Law of Sines to find the lengths of the other sides. If we know all three sides of a triangle, we can use the Law of Cosines to find the measures of the angles. In some cases, we may need to use multiple trigonometric functions to solve a triangle.
Once we have determined the values of the unknown angles and sides, we can round the answers to the nearest tenth as specified. This helps to provide a more precise measurement of the triangle. Solving triangles using trigonometric functions is a valuable tool in mathematics and can be applied to various real-world scenarios, such as engineering, surveying, and navigation.
Applying the Law of Sines to Solve Triangles
The Law of Sines is a useful trigonometric formula that can be applied to solve triangles in various situations. This law relates the lengths of the sides of a triangle to the sines of its angles. By utilizing this law, we can calculate missing side lengths or angles in a triangle.
To apply the Law of Sines, we need to have either two sides and an angle opposite one of the given sides, or two angles and a side opposite one of the given angles. This information allows us to set up an equation using the Law of Sines and solve for the unknown values.
When applying the Law of Sines, it’s important to keep in mind that there can be multiple possible solutions for a triangle. In these cases, we need to consider the ambiguous case, where we may have two possible triangles that satisfy the given information. Additional information or constraints may be needed to determine the unique solution.
To solve a triangle using the Law of Sines, we typically follow these steps:
- Identify the given information, such as side lengths or angles, and label them accordingly.
- Set up the Law of Sines equation, using the known values and the appropriate ratios.
- Solve the equation for the unknown values using algebraic manipulation or a calculator.
- Check for any possible ambiguities or multiple solutions.
- Round the answers to the nearest tenth or as specified in the problem.
By applying the Law of Sines correctly, we can confidently solve triangles and find the missing side lengths or angles. This helps in various fields, such as engineering, navigation, and architecture, where knowledge of triangle properties is essential.
Utilizing the Law of Cosines to Solve Triangles
The Law of Cosines is a fundamental trigonometric equation that allows us to solve triangles when we have specific information about the side lengths and angles. It is particularly useful when we are given two side lengths and the included angle, known as the SSS (side-side-side) case. By applying the Law of Cosines, we can determine the remaining side lengths and angles of the triangle.
The Law of Cosines states that in a triangle with sides a, b, and c, and angle C opposite side c:
c^2 = a^2 + b^2 – 2ab * cos(C)
We can use this equation to solve for any unknown side or angle in the triangle. For example, if we are given the lengths of sides a and b, and the measure of angle C, we can plug these values into the equation and solve for side c. Similarly, if we know the lengths of sides b and c, and the measure of angle A, we can solve for side a.
To solve for an angle, we rearrange the equation to isolate the cosine term. Once we have the cosine value, we can use the inverse cosine function (cos^-1) to find the measure of the angle. This allows us to determine all the angles in the triangle.
In summary, the Law of Cosines is a powerful tool that enables us to solve triangles when given specific information about side lengths and angles. By utilizing this equation, we can accurately determine the missing sides and angles of a triangle, rounding our answers to the nearest tenth if required.
Solving Real-Life Problems Involving Triangles
Triangles are not just a mathematical concept, but they also have practical applications in real-life problems. Whether it’s measuring the height of a building or calculating the distance between two objects, understanding how to solve triangle problems can be useful in various scenarios.
One of the most common real-life problems involving triangles is finding the unknown side length or angle measurement. For example, let’s say you have a ramp that needs to be installed at a certain angle to ensure safety. By knowing the height and base length of the ramp, you can use trigonometric functions such as sine, cosine, and tangent to calculate the angle needed for the installation.
Another practical application is in navigation. Suppose you’re planning a road trip and want to determine the distance between two cities. By using the Law of Cosines or the Law of Sines, you can solve the triangle formed by the two cities and a third point (such as your current location) to find the distance. This information can help you plan your route and estimate travel time.
In construction and architecture, solving triangle problems is essential. Architects and engineers often use trigonometry to calculate the angles and side lengths of structures. For instance, they may need to find the height of a building by measuring the shadow it casts at a certain time of the day and using the concept of similar triangles.
Overall, understanding how to solve triangle problems can be beneficial in various real-life situations. Whether it’s determining angles for safety, finding distances for navigation, or calculating measurements in construction, applying trigonometry principles can help solve practical problems and make informed decisions.
Rounding Answers to the Nearest Tenth for Accuracy
When solving triangles, it is important to round our answers to the nearest tenth for accuracy. Rounding to the nearest tenth means that we are approximating the answer to one decimal place, which allows for a more precise representation of the solution. It helps us avoid unnecessary decimal places and makes the answer easier to work with.
There are two main methods for rounding to the nearest tenth. The first method is the “midpoint rounding” or “round half up” method. In this method, if the number to be rounded is followed by a number greater than or equal to five, we round the number up. If the number is followed by a number less than five, we round the number down. For example, if we have 3.46, we round it up to 3.5.
The second method is the “rounding half to even” or “bankers’ rounding” method. In this method, if the number to be rounded is followed by a number that is exactly five, we round the number to the nearest even number. For example, if we have 3.45, we round it down to 3.4, as four is an even number.
It is important to note that when dealing with angles, we round the answers to the nearest whole number. This is because angles are typically measured in whole number degrees and using decimal places for angles can introduce unnecessary complexity and confusion.
In conclusion, rounding our answers to the nearest tenth allows us to achieve a more accurate representation of the solution when solving triangles. It helps us simplify our calculations and makes our answers easier to work with. By using the appropriate rounding method, we can ensure that our rounded answers are as precise as possible.