Exponential equations are an essential part of algebraic calculations, and understanding how to solve them is crucial for students studying mathematics. Solving exponential equations with the same base can become challenging, as it requires applying various mathematical techniques and reasoning skills. To help students practice and gain confidence in solving such equations, teachers often provide worksheets with a range of exercises and corresponding answers.
These worksheets typically present students with a set of exponential equations that share the same base but have different exponents. Students are required to find the value of the variable by manipulating the given equation and applying appropriate algebraic operations. The answers provided alongside the equations serve as a reference for students to check their work and verify their solutions.
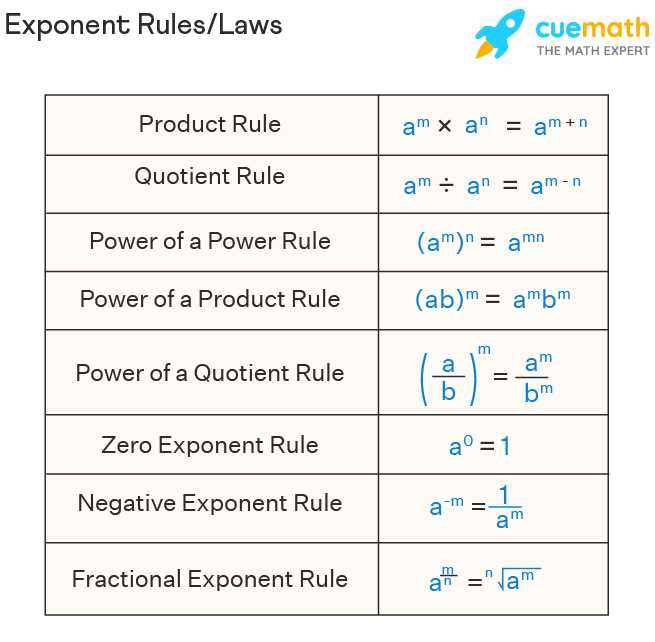
By using these worksheets, students can familiarize themselves with different types of exponential equations, including those with positive and negative exponents. They can also practice applying rules, such as the product of powers, power of a power, and power of a product, to simplify the equations and find the values of the variables. Additionally, solving these equations allows students to strengthen their problem-solving skills and develop a deeper understanding of how exponential functions work.
Overall, solving exponential equations with the same base using worksheet answers serves as a valuable tool for students to practice and master this mathematical concept. By offering a range of exercises and providing answers for reference, these worksheets help students build their problem-solving skills and gain confidence in tackling complex algebraic equations.
Solving Exponential Equations Same Base Worksheet Answers
Exponential equations are equations that contain variables in exponents. Solving these equations can sometimes be tricky, but with practice, it becomes easier. Solving exponential equations with the same base can be simplified using the property that if the bases are the same, then the exponents must also be equal.
When solving exponential equations with the same base, the goal is to isolate the variable by manipulating the exponents. This can be done by taking the logarithm of both sides of the equation with the same base as the exponential expression. By using logarithmic properties, the exponential equation can be rewritten as a logarithmic equation.
Once the equation is in logarithmic form, the variable is isolated and can be solved by simplifying the equation and applying further logarithmic properties if necessary. After finding the value of the variable, it is important to check the solution in the original equation to ensure it is valid.
In a worksheet on solving exponential equations with the same base, the answers would typically include the step-by-step process of simplifying the equation, applying logarithmic properties, isolating the variable, and finding the solution. The answers would also include any necessary checks to verify the validity of the solution.
Understanding Exponential Equations

An exponential equation is an equation that involves an unknown variable in the exponent. These equations are commonly used in various fields of science, such as physics, chemistry, and finance. Understanding how to solve exponential equations is essential for solving problems and making predictions based on exponential growth or decay.
To solve an exponential equation, it is important to know the rules of exponents. One key rule is that if two exponential expressions have the same base, then their exponents must be equal. This rule allows us to equate two exponential expressions and solve for the unknown variable.
For example, consider the equation (2^x = 8). To solve for (x), we can rewrite both sides of the equation using the same base, such as (2^x = 2^3), since (8 = 2^3). By equating the exponents, we find that (x = 3), and we have solved the exponential equation.
It is also important to note that exponential equations can have multiple solutions or no solution at all. In cases where the base is a positive real number, such as (2) or (e), the exponential function is always increasing, and the equation may have a unique solution. However, when the base is a negative number, the exponential function is always decreasing, and the equation may have no solution or infinitely many solutions.
Overall, understanding exponential equations and knowing how to solve them is crucial for analyzing and modeling various real-world phenomena. By mastering the principles behind exponential equations, we can make accurate predictions and solve complex problems in fields that rely on exponential growth or decay.
Common Mistakes in Solving Exponential Equations
When solving exponential equations, it is important to be aware of common mistakes that students often make. These mistakes can lead to incorrect answers and a misunderstanding of the concepts involved. Here are some common errors to watch out for when solving exponential equations:
1. Forgetting to apply the exponent rules:
Exponents have specific rules that need to be followed when solving equations. One common mistake is forgetting to apply these rules, such as multiplying exponents when multiplying terms with the same base. It is important to review and understand exponent rules before attempting to solve exponential equations.
2. Incorrectly isolating the exponential term:
When solving exponential equations, it is essential to isolate the exponential term on one side of the equation. However, students often make mistakes and isolate the wrong term or forget to isolate the exponential term altogether. This can lead to incorrect solutions. It is crucial to carefully perform the necessary steps to isolate the exponential term correctly.
3. Misusing the properties of logarithms:
Some exponential equations can be solved using logarithms. However, students often misapply the properties of logarithms, leading to errors in their solutions. It is important to review the properties of logarithms and understand how they can be used to solve exponential equations. Take the time to practice using logarithmic properties correctly.
4. Incorrectly setting up the equation:
Setting up the equation correctly is crucial when solving exponential equations. Students often make mistakes in identifying and translating the given information into the correct equation. It is important to carefully read the problem, identify the exponential relationship, and set up the equation accurately. Double-checking the equation before solving can help prevent errors.
5. Not checking solutions for extraneous solutions:
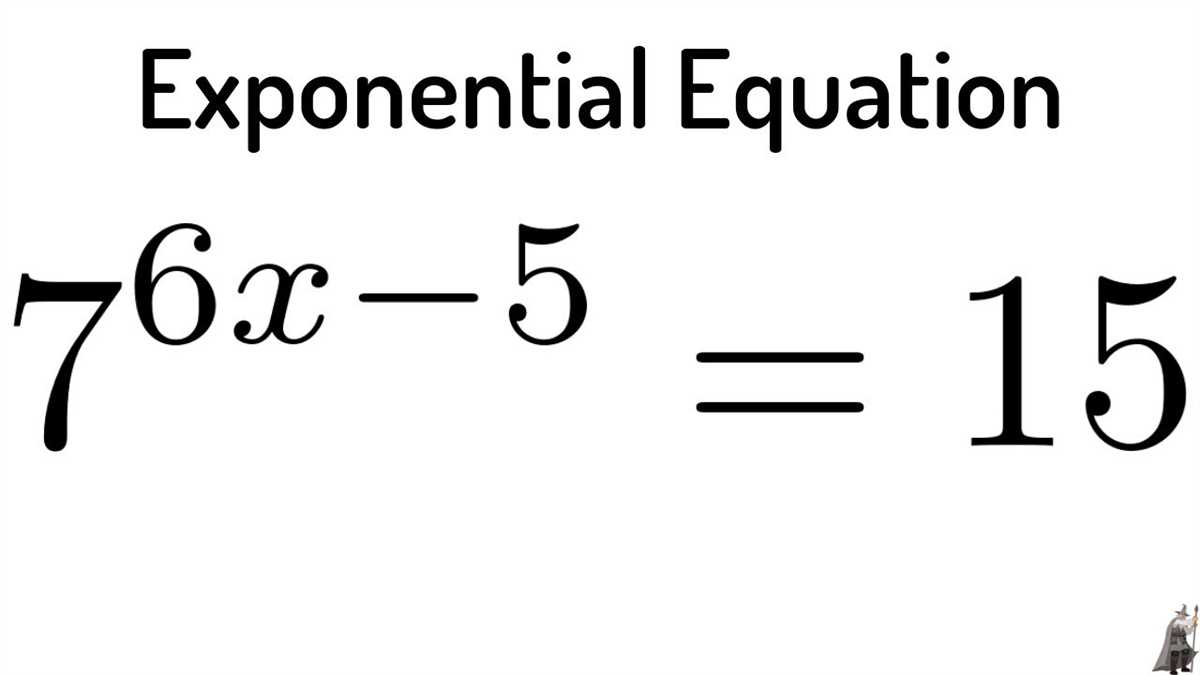
Sometimes, when solving exponential equations, extraneous solutions may arise. These are solutions that satisfy the equation but do not satisfy the original problem. Students often forget to check their solutions and may end up with incorrect answers. It is essential to always check the solutions obtained and verify their validity in the context of the problem.
- Overall, solving exponential equations requires careful attention to details and the application of specific rules and properties.
- Avoiding the common mistakes mentioned above can help ensure accurate solutions and a better understanding of the underlying concepts.
Step-by-Step Solution to Exponential Equations
When solving exponential equations with the same base, it is important to follow a step-by-step process to find the solution. This process involves isolating the variable by manipulating the equation using logarithmic properties.
Step 1: Identify the base
In the given equation, identify the base of the exponential term. This base will be used to calculate logarithms.
Step 2: Take the logarithm of both sides
Apply the logarithm function with the same base as the exponential term to both sides of the equation. This will allow you to bring down the exponent as a coefficient.
Step 3: Simplify the equation
Using the properties of logarithms, simplify the equation by combining like terms and rearranging the equation if necessary.
Step 4: Solve for the variable
Once the equation is simplified, isolate the variable by performing any necessary algebraic operations. This may involve dividing both sides of the equation by a coefficient or raising both sides to a power.
Step 5: Check the solution
After solving for the variable, substitute the solution back into the original equation to ensure it satisfies the equation. If the solution does not work, recheck the steps for errors or consider other possible solutions.
By following these steps, you can systematically solve exponential equations with the same base and find accurate solutions. Practice and familiarity with logarithmic properties and algebraic manipulation will help in solving these equations efficiently.
Practice Problems with Solutions
Here are some practice problems with solutions for solving exponential equations with the same base:
Problem 1:
Solve the equation 2x = 8.
Solution:
- Write both sides of the equation with the same base: 2x = 23.
- Since the bases are the same, set the exponents equal to each other: x = 3.
Therefore, the solution to the equation is x = 3.
Problem 2:
Solve the equation 102x = 100.
Solution:
- Write both sides of the equation with the same base: 102x = 102.
- Since the bases are the same, set the exponents equal to each other: 2x = 2.
- Divide both sides of the equation by 2: x = 1.
Therefore, the solution to the equation is x = 1.
These practice problems demonstrate the process of solving exponential equations with the same base. By writing both sides of the equation with the same base and setting the exponents equal to each other, you can easily find the solution. Remember to check your answers by substituting them back into the original equation before finalizing your solution.
Advanced Techniques for Solving Exponential Equations

Exponential equations are equations in which the variable appears in an exponent. Solving exponential equations can be challenging, but with advanced techniques, it is possible to find the solution.
One of the advanced techniques for solving exponential equations with the same base is using logarithms. By taking the logarithm of both sides of the equation, the exponential equation can be transformed into a logarithmic equation. For example, if we have the equation (2^x = 8), we can take the logarithm base 2 of both sides to get (log_2(2^x) = log_2(8)). This simplifies to (x = log_2(8)), which can be further simplified to (x = 3).
Another advanced technique for solving exponential equations is using the properties of exponents. If the equation involves exponential expressions with the same base, the exponent rule ((a^x)^y = a^{xy}) can be applied. This rule allows us to simplify the equation by simplifying the exponents. For example, if we have the equation (5^{2x + 1} = 5^3), we can apply the exponent rule to get (2x + 1 = 3). From here, we can solve for (x) by subtracting 1 from both sides and then dividing by 2, giving us (x = 1).
Overall, solving exponential equations with the same base requires advanced techniques such as using logarithms and the properties of exponents. By applying these techniques, it is possible to find the solutions to exponential equations and further understand the behavior of exponential functions.
Real-Life Applications of Exponential Equations
Exponential equations have a wide range of applications in real-life scenarios. These equations are often used to model exponential growth or decay, which can be observed in various fields and industries. By understanding and solving exponential equations, we can make predictions, analyze data, and make informed decisions in these areas.
Here are some examples:
- Finance and Investments: Exponential equations are used to model compound interest, which is the exponential growth of an initial investment over time. Understanding these equations can help individuals and businesses calculate the future value of investments and make informed financial decisions.
- Population Growth and Demographics: Exponential equations are often used to model population growth. By analyzing population data and using exponential equations, researchers can predict future population trends, plan for resource allocation, and study the impact of policies and interventions.
- Radioactive Decay: Exponential equations are used in nuclear physics to model the decay of radioactive materials. Scientists use these equations to determine the half-life of a radioactive substance, which is critical in fields such as nuclear energy, radiology, and carbon dating.
- Epidemiology and Disease Spread: Exponential equations play a crucial role in modeling the spread of infectious diseases. By understanding the rate of infection and using exponential equations, epidemiologists can predict the number of cases, evaluate the effectiveness of interventions, and make informed decisions to control the spread of diseases.
In conclusion, exponential equations have numerous real-life applications across various fields. Understanding and solving these equations allow us to make predictions, analyze data, and make informed decisions in finance, population growth, radioactive decay, and epidemiology. By utilizing exponential equations, we can better understand and navigate the complexities of our world.