In mathematics, the surface area is the total area of the outer surface of a three-dimensional object. When it comes to prisms and cylinders, finding the surface area can be a bit tricky. That’s why having an answer key that provides step-by-step solutions is extremely helpful for students.
Understanding how to calculate the surface area of prisms and cylinders is important, as it allows us to determine how much material is needed to cover the object. This is particularly useful in real-life situations, such as when planning to paint a room or wrap a gift.
This answer key provides detailed explanations of the formulas used to find the surface area of prisms and cylinders, as well as a variety of example problems to practice with. By following the step-by-step solutions, students can gain a better understanding of the concepts and improve their problem-solving skills.
What is surface area and why is it important?
Surface area is the total area of all the faces of a three-dimensional object. It is an important concept in geometry as it helps us understand and quantify the amount of material needed to cover or wrap an object, as well as calculate the amount of heat transfer that can occur between the object and its surroundings. Knowing the surface area of an object is crucial in various real-life applications, such as construction, architecture, manufacturing, and engineering.
The surface area of an object is calculated by finding the area of each individual face and then adding them together. For example, a rectangular prism has six rectangular faces, so to find its surface area, we would calculate the area of each face and sum them up. Similarly, a cylinder has two circular faces and a curved surface, so its surface area would involve finding the areas of those three components and adding them together.
Understanding surface area is important because it helps us solve practical problems related to objects in the real world. For instance, if we want to paint a room, knowing the surface area of the walls will help us determine how much paint we need to buy. Similarly, when designing packaging for a product, knowing the surface area of the package will help ensure that we have enough material to cover it. Surface area also plays a role in heat transfer calculations, as the larger the surface area of an object, the more heat it can exchange with its surroundings.
In conclusion, surface area is a fundamental concept in geometry that allows us to quantify the total area of all the faces of a three-dimensional object. It is important in various practical applications, including construction, manufacturing, and heat transfer calculations. By understanding and calculating surface area, we can effectively solve problems and make informed decisions in real-life situations.
Understanding Prisms: Definition, Properties, and Formulas

A prism is a three-dimensional geometric shape that is formed by two parallel bases connected by rectangular or parallelogram faces. Prisms are classified based on the shape of their bases, such as triangular prisms, rectangular prisms, or pentagonal prisms. Understanding the properties and formulas related to prisms is essential in mathematics and engineering.
Definition: A prism is a polyhedron with two congruent, parallel faces called bases, and its remaining faces are parallelograms.
Properties: There are several key properties of prisms:
- Prisms have two congruent bases that are polygons.
- The faces that connect the bases are rectangles or parallelograms.
- The lateral faces of a prism are always perpendicular to the bases.
- The altitude of a prism is the perpendicular distance between the bases.
- The lateral edges of a prism are congruent.
Formulas: The formulas to calculate the surface area and volume of prisms depend on the shape of their bases.
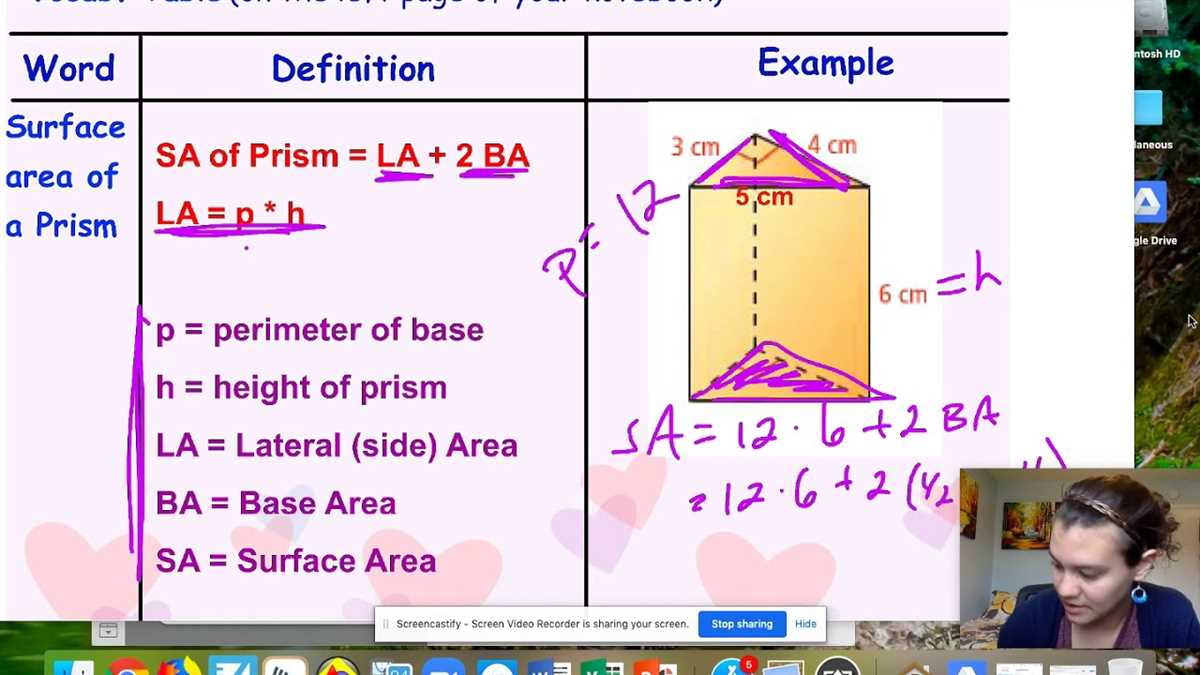
- Surface Area: The surface area of a prism is calculated by adding the areas of the two bases to the sum of the areas of all the lateral faces. The general formula for the surface area of a prism is: SA = 2B + L, where SA is the surface area, B is the area of the base, and L is the sum of the lateral face areas.
- Volume: The volume of a prism is calculated by multiplying the area of the base by the height (altitude) of the prism. The general formula for the volume of a prism is: V = Bh, where V is the volume, B is the area of the base, and h is the height (altitude) of the prism.
Understanding prisms and their properties is crucial for solving problems related to surface areas and volumes in geometry and engineering. The formulas provided can be used to calculate the surface area and volume of prisms accurately and efficiently.
Calculating the surface area of a prism: step-by-step guide
Calculating the surface area of a prism is an important skill in geometry. In this step-by-step guide, we will walk you through the process of finding the surface area of a prism, using the formula:
Surface Area = 2 * base area + lateral area
Step 1: Identify the shape of the base
The first step in calculating the surface area of a prism is to identify the shape of its base. This could be a square, rectangle, triangle, or any other polygon. Once you have determined the shape of the base, you can move on to the next step.
Step 2: Calculate the base area
Next, calculate the area of the base. This can be done by using the appropriate formula for the shape of the base. For example, if the base is a rectangle, the formula for its area is length * width. If the base is a triangle, the formula is 0.5 * base * height. Calculate the area and write down the result.
Step 3: Calculate the lateral area

The lateral area of a prism refers to the sum of the areas of all the lateral faces, excluding the base. To calculate the lateral area, you need to know the height of the prism and the length of each lateral face. Multiply the perimeter of the base by the height to find the lateral area of one face, and then multiply that by the number of lateral faces. Write down the result.
Step 4: Plug the values into the formula
Finally, plug the values you calculated for the base area and lateral area into the formula for surface area. Multiply the base area by 2, add the lateral area, and you will have the surface area of the prism.
By following these four steps, you can easily calculate the surface area of any prism. Remember to double-check your calculations and units to ensure accuracy.
Working with cylinders: properties and formulas
Cylinders are three-dimensional geometric shapes that have two parallel circular bases connected by a curved lateral surface. Understanding the properties and formulas associated with cylinders is essential for calculating their surface areas and volumes.
A cylinder has several important properties. First, the bases of a cylinder are congruent circles, which means they have the same size and shape. Second, the axis of a cylinder is a line that connects the center points of the two bases. This axis is also the longest segment that can be drawn through the cylinder. Third, the height of a cylinder is the perpendicular distance between the two bases and is denoted by “h”. Finally, the radius of a cylinder is the distance from the center of either base to any point on the circumference and is denoted by “r”.
When working with cylinders, there are two main formulas to remember: one for the surface area and one for the volume. The formula for the surface area of a cylinder is:
Surface Area = 2πr(r + h)
This formula accounts for the surface area of the two bases (πr^2) and the curved lateral surface (2πrh). By plugging in the values for the radius and height of a cylinder, you can calculate its total surface area.
The formula for the volume of a cylinder is:
Volume = πr^2h
This formula calculates the amount of space inside the cylinder. By multiplying the area of the base (πr^2) by the height (h), you can determine the volume of the cylinder.
Understanding these properties and formulas is essential for solving problems related to the surface areas and volumes of cylinders. By applying these concepts, you can accurately calculate and analyze the properties of these three-dimensional shapes in various real-world and mathematical contexts.
Step-by-step instructions for finding the surface area of a cylinder
A cylinder is a three-dimensional shape that has two circular bases connected by a curved surface. To find the surface area of a cylinder, we need to calculate the areas of both circular bases and the area of the curved surface, and then add them up.
Step 1: Measure the height of the cylinder. This is the distance between the two circular bases.
Step 2: Measure the radius of one of the circular bases. This is the distance from the center of the base to its outer edge.
Step 3: Calculate the area of one circular base. The formula to find the area of a circle is A = πr^2, where A is the area and r is the radius.
Step 4: Multiply the area of one circular base by 2 to get the total area of both bases.
Step 5: Calculate the area of the curved surface. The formula to find the area of a rectangle is A = 2πrh, where A is the area, π is a mathematical constant (approximately 3.14159), r is the radius of the circular base, and h is the height of the cylinder.
Step 6: Add the area of both bases and the area of the curved surface to find the total surface area of the cylinder.
Step 7: Round the final result to the desired level of precision, if necessary.
By following these step-by-step instructions, you can easily find the surface area of a cylinder.
Common Mistakes and Troubleshooting Tips
When solving problems involving surface areas of prisms and cylinders, it’s easy to make some common mistakes. Here are a few tips to help you avoid these mistakes and troubleshoot your work if you encounter any issues:
Mistake #1: Forgetting to multiply by the height of the prism or cylinder

One of the most common mistakes is to forget to multiply the surface area of the base by the height of the prism or cylinder. Remember that the formula for the surface area of a prism is 2B + Ph, where B is the base area and P is the perimeter of the base. Similarly, the formula for the surface area of a cylinder is 2πrb + 2πrh, where rb is the radius of the base and h is the height.
Troubleshooting Tip: Check your calculations
If you’re not getting the expected answer, double-check your calculations. Make sure you’ve used the correct formulas and correctly calculated the base area, perimeter, radius, and height. Check your work for any errors in multiplication, addition, or subtraction.
Mistake #2: Not accounting for the curved surface area of a cylinder

Another common mistake is forgetting to include the curved surface area of a cylinder in the total surface area calculation. Remember that the formula for the total surface area of a cylinder is the sum of the curved surface area and the areas of the two bases. So, it’s important to include the term 2πrh in your calculation.
Troubleshooting Tip: Verify your formulas
If your answer seems too small or doesn’t make sense, check your formulas to ensure you’re including all the necessary components. Verify that you’ve correctly included the curved surface area term and that you’re adding it to the areas of the bases.
Mistake #3: Using the wrong units
Using the wrong units can also lead to errors in surface area calculations. Make sure you’re using consistent units throughout your work. If necessary, convert units to match. For example, if the height is given in inches, but the base area is given in square feet, you’ll need to convert the height to the same unit (feet) before multiplying it by the base area.
Troubleshooting Tip: Check your units
If your answer seems unusually large or doesn’t align with the given units, double-check your units. Make sure they’re consistent and that you’ve converted any necessary values to match.
To summarize, it’s important to remember to multiply by the height, account for the curved surface area of a cylinder, and use consistent units when calculating surface areas of prisms and cylinders. By being mindful of these common mistakes and using the provided troubleshooting tips, you can ensure accurate and reliable results in your work.