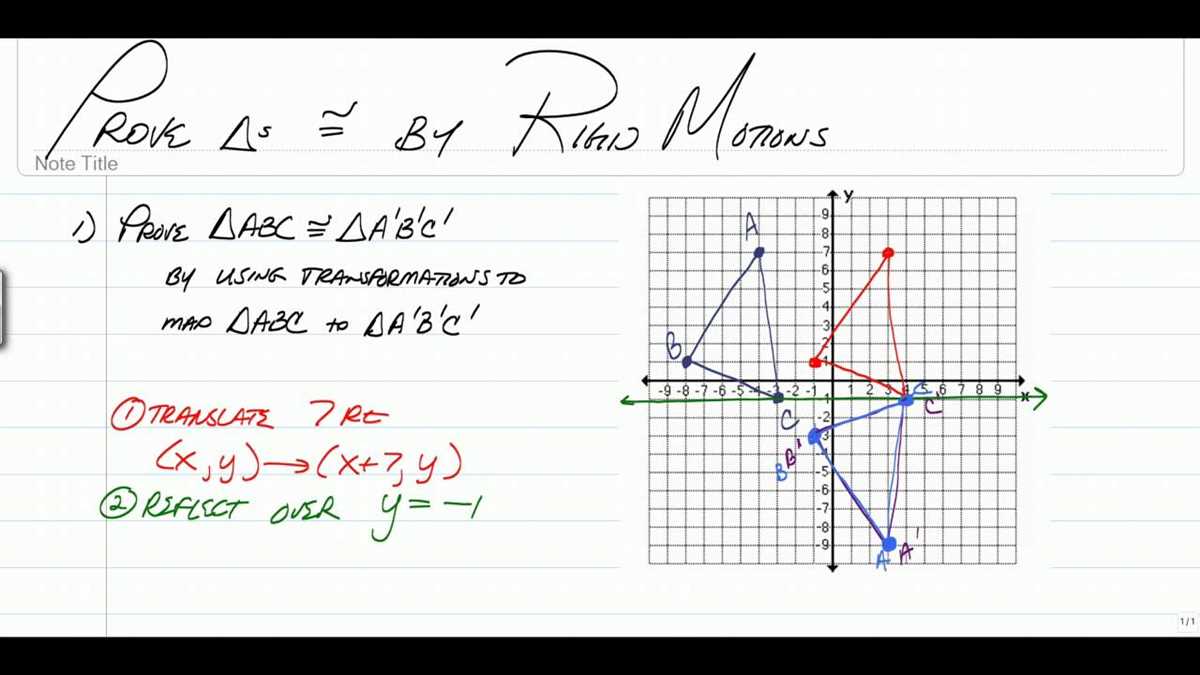
In Topic 1 of geometry, students learn about rigid motion transformations, which involve moving and rotating figures on a coordinate plane without changing their shape or size. These transformations are essential in understanding the properties and relationships of geometric shapes and are used in various real-life applications, such as computer graphics and robotics.
One important concept in rigid motion transformations is the idea of congruence. Congruent figures are identical in shape and size, and can be obtained by applying a series of rigid motions to a given figure. By understanding the properties of rigid motions, students can determine if two figures are congruent and solve problems involving congruence.
To fully grasp the topic, students need to practice applying different rigid motions, such as translations, rotations, and reflections. The answer key for Topic 1 provides solutions to the exercises and problems related to these rigid motions. It serves as a valuable resource for both students and teachers, allowing them to check their work, verify their understanding, and identify any mistakes they may have made.
By using the provided answer key, students can gain confidence in their ability to perform rigid motions and solve related problems. It also helps teachers assess students’ progress and guide their instruction accordingly. Overall, the answer key for Topic 1 rigid motion transformations plays a crucial role in supporting students’ learning and mastery of this fundamental geometric concept.
What Are Rigid Motion Transformations?
Rigid motion transformations are mathematical operations that preserve the shape and size of an object. These transformations include translations, rotations, and reflections. They are often used in geometry to describe how an object can be moved or transformed without changing its overall appearance.
Translations: One type of rigid motion transformation is a translation, which involves moving an object in a specific direction without changing its shape or size. This is done by shifting the object along a vector, such as moving it horizontally or vertically.
Rotations: Another type of rigid motion transformation is a rotation, which involves rotating the object around a fixed point. This rotation can be clockwise or counterclockwise, and the angle of rotation determines how much the object is turned.
Reflections: A third type of rigid motion transformation is a reflection, which involves flipping the object over a line of symmetry. This creates a mirror image of the object, but does not change its shape or size.
Rigid motion transformations are important in geometry because they allow us to describe how objects can be moved or transformed while maintaining their original properties. They help us understand the concept of symmetry and provide a basis for more complex geometric calculations and constructions.
Defining Rigid Motion Transformations
Rigid motion transformations, also known as isometries, are mathematical operations that preserve the shape and size of an object. These transformations include translations, rotations, and reflections, and they are commonly used in geometry to describe how an object moves or changes position.
A translation is a rigid motion transformation that moves an object from one location to another without changing its orientation or shape. It involves moving every point of the object by a fixed distance and direction. For example, if we have a rectangle and we translate it 3 units to the right and 2 units up, every point of the rectangle will be shifted by those amounts.
A rotation is another type of rigid motion transformation that involves turning an object around a fixed point. The object remains the same shape and size, but its orientation changes. Rotations can be clockwise or counter-clockwise, and they are described by the angle and direction of the turn. For instance, if we rotate a square 90 degrees clockwise around its center, all its points will be rotated by that amount.
A reflection is a rigid motion transformation that creates a mirror image of an object. It involves flipping the object across a line called the line of reflection. The shape and size of the object are preserved, but its orientation is reversed. For example, if we reflect a triangle across a vertical line, the resulting image will be an identical triangle but facing the opposite direction.
In summary, rigid motion transformations are mathematical operations that preserve the shape and size of an object. Translations move the object without changing its orientation, rotations turn the object around a fixed point, and reflections create mirror images. These transformations are fundamental concepts in geometry and are used to describe the motion and position of objects.
Types of Rigid Motion Transformations
Rigid motion transformations are a fundamental concept in geometry and play a crucial role in various mathematical applications. They refer to transformations that preserve the shape and size of objects, maintaining their distances and angles.
There are several types of rigid motion transformations, each characterized by its specific properties and applications:
- Translation: A translation is a type of rigid motion transformation that slides an object in a specific direction without changing its orientation. It preserves the distances between points and is described by a vector that represents the displacement.
- Rotation: Rotation is another type of rigid motion transformation that involves rotating an object around a fixed point or axis. It preserves the distances between points and the orientation of the object, but the shape may appear differently depending on the angle and direction of rotation.
- Reflection: Reflection is a rigid motion transformation that involves flipping an object over a line called the line of reflection. It preserves the distances between points but reverses their orientation. Reflection can occur horizontally, vertically, or obliquely.
- Glide Reflection: Glide reflection is a combination of a reflection and a translation. It involves reflecting an object over a line and then translating it parallel to the line of reflection. This transformation preserves the shape and size of the object but changes its position.
These types of rigid motion transformations are essential in geometry as they allow us to understand how objects can be transformed in space while preserving their fundamental properties. They are used in various branches of mathematics, engineering, computer graphics, and physics to model and analyze the behavior of objects and their transformations.
Properties of Rigid Motion Transformations
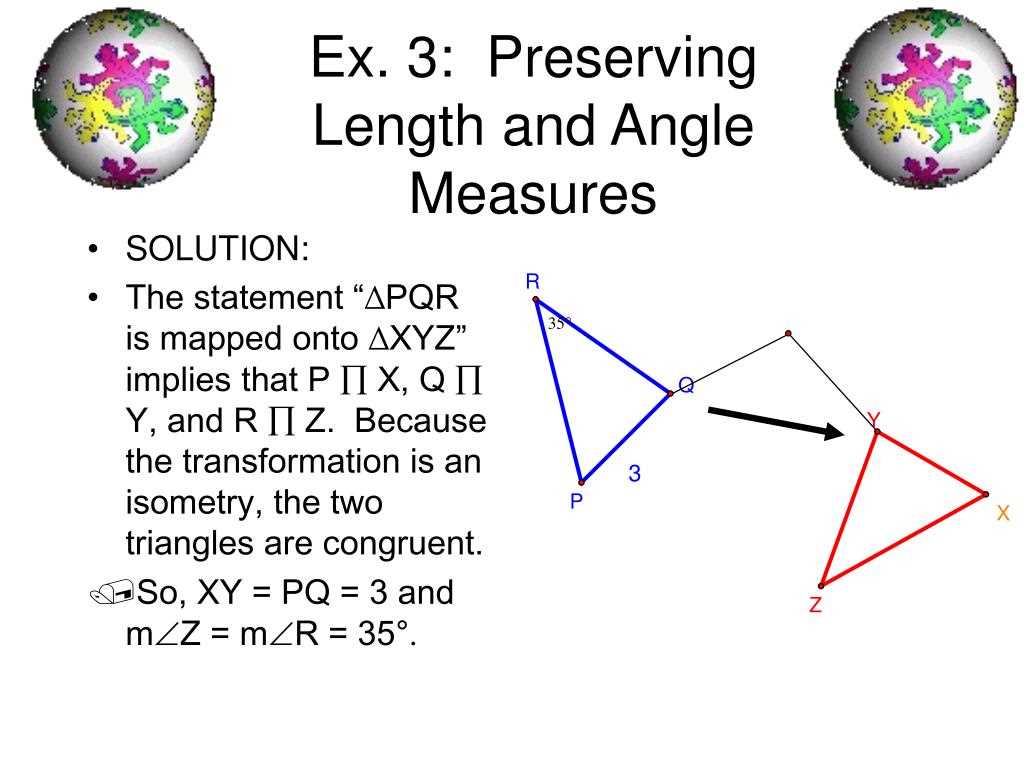
Rigid motion transformations are geometric transformations that preserve the size and shape of an object. These transformations include translations, rotations, and reflections. Each type of transformation has its own unique properties and characteristics.
Translations: Translations involve moving an object from one location to another without changing its size or shape. The properties of translations include:
- They do not change the lengths of the sides or angles of the object.
- They preserve the orientation of the object.
- They are characterized by a vector or an arrow that specifies the amount and direction of the translation.
Rotations: Rotations involve rotating an object around a fixed point, known as the center of rotation. The properties of rotations include:
- They preserve the lengths of the sides and angles of the object.
- They preserve the orientation of the object.
- They are characterized by the degree of rotation and the center of rotation.
Reflections: Reflections involve flipping an object over a line of reflection. The properties of reflections include:
- They preserve the lengths of the sides of the object, but the angles may change.
- They reverse the orientation of the object.
- They are characterized by the line of reflection.
Overall, rigid motion transformations are powerful tools in geometry that allow us to manipulate and analyze objects while preserving their essential properties. By understanding the properties of each type of transformation, we can solve problems and explore the relationships between different geometric figures.
How to Perform Rigid Motion Transformations

Rigid motion transformations are mathematical operations that preserve the shape and size of an object. These transformations include translation, rotation, and reflection. Performing these transformations involves following specific steps to accurately move or rotate an object in a coordinate plane
Translation: To perform a translation, you need to move an object a certain distance in a specific direction without changing its shape or size. Start by determining the direction and distance of the translation. Then, apply the translation by shifting each point of the object the specified distance in the given direction.
Rotation: Rotating an object involves turning it around a fixed point, known as the center of rotation. To perform a rotation, start by identifying the center of rotation and the angle of rotation. Then, apply the rotation by calculating the new coordinates of each point using the rotation matrix or formulas.
Reflection: Reflecting an object involves flipping it over a line, known as the line of reflection. To perform a reflection, start by identifying the line of reflection. Then, apply the reflection by finding the mirror image of each point across the line of reflection. This can be done by calculating the distance between the original point and the line of reflection, and then moving the point across the line by the same distance.
By following these steps and using the appropriate formulas or matrices, you can accurately perform rigid motion transformations on geometric objects in a coordinate plane. Practice and familiarize yourself with the concepts and calculations involved to become proficient in performing these transformations.
Applications of Rigid Motion Transformations
Rigid motion transformations, also known as isometries, are mathematical operations that preserve the shape and size of an object. These transformations include translations, rotations, and reflections. They are widely used in various fields to represent and analyze geometric shapes and structures.
One important application of rigid motion transformations is in computer graphics and animation. By applying these transformations to the vertices of a 3D model, designers can create realistic motion and movement in virtual environments. For example, a rotation transformation can be used to simulate the movement of a character’s arm, while a translation transformation can be used to animate an object moving across the screen.
In the field of architecture, rigid motion transformations are essential for designing and building structures. Architects use these transformations to manipulate and position building components accurately. For instance, a translation transformation can be employed to shift an entire floor plan or a specific element within a structure. Additionally, rotations can be used to align walls or adjust the orientation of doors and windows.
Rigid motion transformations also have applications in the field of robotics. By applying these transformations to the joints of a robot arm, engineers can control its movement and position precisely. This allows robots to perform tasks such as pick-and-place operations or assembly tasks with high accuracy.
In conclusion, rigid motion transformations play a crucial role in various areas, including computer graphics, architecture, and robotics. Their ability to preserve shape and size while allowing for precise manipulation makes them invaluable tools in representing and analyzing geometric objects and structures.
Rigid Motion Transformations Answer Key
In conclusion, the rigid motion transformations answer key provides a comprehensive solution to understanding and solving problems related to rigid motions in mathematics. It outlines the various types of rigid motions, including translations, rotations, and reflections, and provides step-by-step instructions and examples for performing these transformations.
The answer key also includes explanations of key concepts, such as the properties of rigid motions and how to identify congruent figures. It serves as a valuable resource for students and teachers alike, allowing them to practice and reinforce their understanding of rigid motion transformations.
By using the provided answer key, students can check their own work and identify any errors or misconceptions they may have. It can also be used as a teaching tool, allowing teachers to demonstrate the correct methods and strategies for solving problems involving rigid motion transformations.
Overall, the rigid motion transformations answer key is an invaluable tool for mastering this important mathematical concept. It provides clear and concise explanations, examples, and exercises that aid in the understanding and application of rigid motion transformations. Whether used by students for self-study or as a teaching aid in the classroom, the answer key is an essential resource for success in the study of rigid motions.