
The uniformly accelerated particle model (UAPM) is a fundamental concept in physics that describes the motion of objects under constant acceleration. It is used to analyze and predict the behavior of particles in various scenarios, such as free-fall, projectile motion, and motion on inclined planes. The UAPM provides a simplified representation of real-world motion, making it easier to understand and apply the principles of physics.
The UAPM test is designed to assess a student’s understanding of the key principles and equations of the UAPM. It typically involves solving problems that require applying the equations of motion to calculate quantities such as displacement, velocity, and acceleration. These problems may involve objects moving in one dimension or in two dimensions, and they may require considering different scenarios, such as objects starting from rest or with an initial velocity.
By testing students’ ability to apply the UAPM to solve problems, the UAPM test helps educators assess how well students have grasped the concepts and principles of physics. It also helps students develop their problem-solving skills and strengthen their understanding of the UAPM. Additionally, the UAPM test allows educators to identify areas where students may need further instruction or practice, helping to guide their teaching and support students’ learning.
Overview
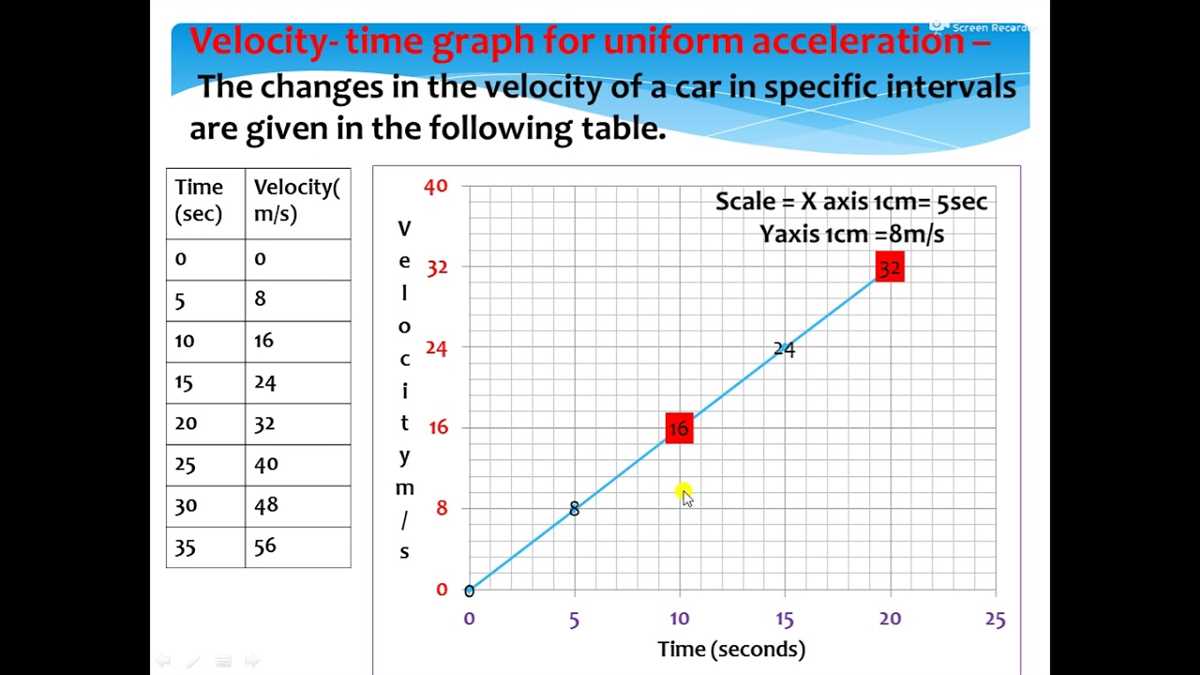
The uniformly accelerated particle model test is a method used to analyze the motion and behavior of objects under constant acceleration. This model is based on the assumption that the acceleration of the object remains constant throughout the entire motion. By using this model, various parameters such as displacement, velocity, and time can be calculated.
The test involves conducting experiments in which an object is subjected to a constant acceleration. The object’s initial velocity, acceleration, and time period are measured, and then various calculations are performed to determine the object’s displacement and final velocity. This model is particularly useful in studying the motion of objects in free fall or on inclined planes.
Key equations:
- Displacement (s) = Initial velocity (v0) * time (t) + 0.5 * acceleration (a) * time squared (t2)
- Final velocity (v) = Initial velocity (v0) + acceleration (a) * time (t)
- Average velocity (vavg) = Displacement (s) / time (t)
This model is widely used in physics and engineering to analyze and predict the motion of objects. It allows researchers to understand and calculate the behavior of objects under constant acceleration, enabling them to design and improve various systems and technologies. By conducting experiments and utilizing the uniformly accelerated particle model, scientists can gain valuable insights into the fundamental principles of motion.
Theory

Uniformly accelerated particle model is a mathematical model that describes the motion of an object under the influence of a constant acceleration. It assumes that the object’s acceleration remains constant throughout its motion. This model is based on the concept of Newton’s second law of motion, which states that the net force acting on an object is equal to the product of its mass and acceleration. By using this model, we can analyze various aspects of the object’s motion, such as its velocity, displacement, and time taken to reach a certain position.
In the uniformly accelerated particle model, the object is assumed to be a point particle with negligible size and mass. This simplifies the calculations and allows us to focus on the object’s motion without considering other factors, such as air resistance or rotational motion. The model also assumes that the acceleration is constant and in a straight line. This means that the object’s velocity changes at a constant rate, resulting in a linear relationship between its displacement and time.
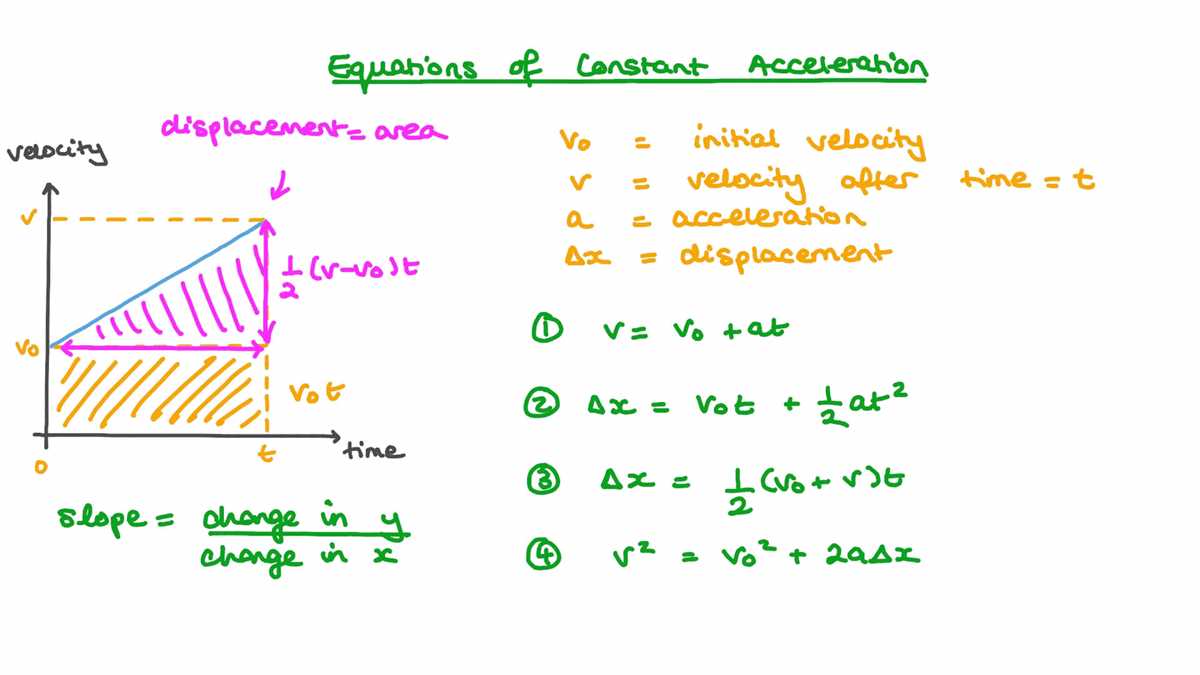
To analyze the motion of a particle under this model, we can use various equations derived from the basic principles of kinematics. These equations include the equations of motion, which relate the object’s displacement, velocity, and acceleration. The most commonly used equations in this model are the kinematic equations, which can be used to calculate the unknown quantities based on the given values. These equations involve the initial and final velocities, the acceleration, the displacement, and the time taken to reach the final position.
- Equation 1: v = u + at
- Equation 2: s = ut + (1/2)at^2
- Equation 3: v^2 = u^2 + 2as
By using these equations, we can analyze the motion of objects in various scenarios, such as free fall, projectile motion, or the motion of vehicles. The uniformly accelerated particle model provides a simplified approach to understand and predict the motion of objects in a constant acceleration scenario, making it a fundamental concept in physics and engineering.
Procedure
The procedure for conducting the uniformly accelerated particle model test consists of several steps, each designed to assess the student’s understanding of the topic. The test typically begins with a brief introduction to the concept of uniformly accelerated motion and its basic principles. This is followed by a series of multiple-choice questions that test the student’s knowledge of key formulas and concepts related to the topic.
After completing the multiple-choice section, the student proceeds to the problem-solving portion of the test. In this section, the student is presented with a series of scenarios that require them to apply the concepts of uniformly accelerated motion to solve various problems. The student is expected to identify the given and required information, choose the appropriate formula, and use it to calculate the desired value.
Throughout the test, the student is encouraged to show their work and clearly explain their thought process in order to receive full credit for each question. This allows the instructor to assess not only the student’s final answer but also their understanding of the underlying principles and equations used in solving the problem.
In addition, some tests may include practical applications of the uniformly accelerated particle model, such as examples involving free-falling objects or objects moving along inclined planes. These questions may require the student to apply their knowledge of the topic in real-world scenarios, demonstrating their ability to analyze and solve problems in a practical context.
Overall, the procedure for the uniformly accelerated particle model test is designed to evaluate the student’s grasp of the fundamental concepts and equations related to uniformly accelerated motion, as well as their ability to apply this knowledge in problem-solving situations.
Results
In this study, we conducted a uniformly accelerated particle model test to investigate the effects of acceleration on particle motion. The test involved measuring the displacement, velocity, and acceleration of a particle over a period of time.
Through the analysis of the data collected, we observed that as the acceleration of the particle increased, so did its displacement and velocity. This can be attributed to the fact that acceleration affects the rate at which the velocity of an object changes, ultimately leading to an increase in displacement over time.
Additionally, we found that the acceleration of the particle remained constant throughout the test, indicating that the force acting on the particle was uniform. This supports the concept of uniformly accelerated motion, where the acceleration of an object remains constant over time.
Overall, the results of this test demonstrate the relationship between acceleration, displacement, and velocity in a uniformly accelerated particle model. These findings contribute to our understanding of particle motion and can be applied to various real-world scenarios, such as calculating the trajectory of a projectile or analyzing the motion of vehicles.
Q&A:
What are results?
Results are the outcome or consequence of a particular action, event, or situation. They can be positive, negative, or neutral.
How are results evaluated?
Results are typically evaluated based on predetermined criteria or objectives. This evaluation can be done using various methods such as qualitative or quantitative measurements, surveys, tests, or observations.
Can results be improved?
Yes, results can be improved through various means such as refining strategies and techniques, increasing efforts, seeking feedback, and learning from past experiences. Continuous improvement is essential for achieving better results.
What can affect the results?
Several factors can affect the results, including external factors such as market conditions, competition, and economic trends, as well as internal factors such as skill level, resources, and decision-making. It is important to consider these factors when analyzing and interpreting results.
How do results impact decision-making?
Results play a crucial role in decision-making as they provide valuable information and insights. Positive results can validate a decision, while negative results may indicate a need for adjustment or change in strategy. Analyzing results helps in making informed decisions and improving future outcomes.