
In mathematics, polynomial functions play a crucial role in understanding and analyzing various phenomena. They are widely used in fields such as physics, engineering, economics, and computer science. A polynomial function is a function of the form f(x) = a_nx^n + a_{n-1}x^{n-1} + … + a_1x + a_0, where n is a non-negative integer and a_n, a_{n-1}, …, a_1, a_0 are constants.
Unit 3 of a polynomial functions course focuses on providing students with the necessary tools and techniques to understand and solve problems related to polynomial functions. The unit covers topics such as factoring polynomials, finding zeros of polynomial functions, graphing polynomial functions, and solving polynomial equations. These skills are essential for further study in calculus and other advanced mathematical disciplines.
This answer key for Unit 3 polynomial functions serves as a valuable resource for both students and educators. It provides step-by-step solutions and explanations for various problems and exercises that students encounter throughout the unit. The answer key helps students check their work, identify any mistakes, and gain a deeper understanding of the concepts and techniques taught in the course.
With the help of this answer key, students can reinforce their understanding of polynomial functions, build their problem-solving skills, and gain the confidence to tackle more complex mathematical problems. Additionally, educators can use the answer key as a teaching aid to facilitate classroom discussions, guide students through problem-solving strategies, and assess their progress and comprehension.
What Is a Polynomial Function?
A polynomial function is a mathematical function that can be written in the form:
f(x) = anxn + an-1xn-1 + … + a1x + a0
Here, f(x) represents the function, an to a0 are constants, and x is the variable. The exponents on x are non-negative integers, and the coefficients an to a0 could be any real numbers, including zero.
Polynomial functions can have different degrees, depending on the highest exponent of x in the function. For example, a polynomial of degree 3 would have terms like x3, x2, x, and a constant term. The degree gives us information about the behavior of the function and the number of roots it has.
Polynomial functions are important in many areas of mathematics and science. They are used to model and represent various real-world phenomena, such as population growth, economic trends, and physical processes. Understanding polynomial functions and their properties is essential for solving equations, finding roots, and analyzing mathematical models.
Understanding the Basics
Polynomial functions are a fundamental concept in mathematics, commonly encountered in algebra and calculus. They are an essential tool for modeling and analyzing various real-life phenomena, such as population growth, economic trends, and physical systems.
A polynomial function is defined as a function in which the variable is raised to a non-negative integer power and is multiplied by a coefficient. The highest power of the variable in a polynomial function is known as the degree of the polynomial. Polynomial functions can have multiple terms, each with a different power of the variable. For example, the function f(x) = 3x^2 – 2x + 1 is a polynomial function of degree 2 with three terms.
In order to understand polynomial functions, it is important to familiarize yourself with several key terms and concepts. The leading coefficient of a polynomial function is the coefficient of the term with the highest power of the variable. The leading term of a polynomial function is the term with the highest power of the variable. The constant term of a polynomial function is the term with no variable.
By analyzing the degree, leading coefficient, and leading term of a polynomial function, we can determine important characteristics such as the end behavior and the number of roots or solutions. The end behavior describes the behavior of the function as x approaches positive or negative infinity. The number of roots or solutions represents the number of values of x for which the function equals zero.
Polynomial functions can be graphed to visualize their behavior and identify important features such as the x-intercepts, y-intercept, and turning points. The x-intercepts are the points at which the function intersects the x-axis, and the y-intercept is the point at which the function intersects the y-axis. Turning points are the points on the graph where the function changes from increasing to decreasing or vice versa.
Overall, understanding the basics of polynomial functions is crucial for solving problems in various fields of science and engineering, as well as for deepening our understanding of mathematical concepts. By grasping the fundamentals and key concepts, we can confidently tackle more complex polynomial functions and their applications.
Common Types of Polynomial Functions
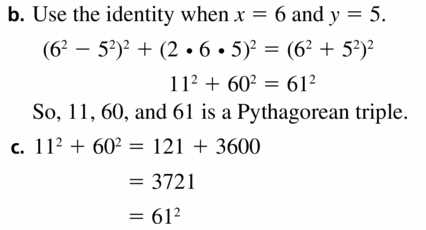
Polynomial functions are mathematical expressions that consist of variables raised to integer exponents and multiplied by coefficients. There are several common types of polynomial functions, each with its own characteristics and uses.
Linear Functions: Linear functions are a type of polynomial function with a degree of 1. They have a constant rate of change and represent straight lines when graphed. Linear functions can be written in the form f(x) = mx + b, where m is the slope of the line and b is the y-intercept.
Quadratic Functions: Quadratic functions are polynomial functions with a degree of 2. They have a parabolic shape when graphed and can have one or two x-intercepts. Quadratic functions can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants.
Cubic Functions: Cubic functions are polynomial functions with a degree of 3. They have an S-shaped curve when graphed and can have up to three x-intercepts. Cubic functions can be written in the form f(x) = ax^3 + bx^2 + cx + d, where a, b, c, and d are constants.
Quartic Functions: Quartic functions are polynomial functions with a degree of 4. They have a variety of shapes when graphed and can have up to four x-intercepts. Quartic functions can be written in the form f(x) = ax^4 + bx^3 + cx^2 + dx + e, where a, b, c, d, and e are constants.
Higher Degree Polynomial Functions: Polynomial functions can have degrees higher than 4, but they become increasingly complex and difficult to graph or analyze. These higher degree polynomial functions can have multiple x-intercepts and complicated curves. They are often used in advanced mathematical and scientific applications.
In summary, polynomial functions come in various types, each with its own degree and characteristics. Linear functions have a degree of 1 and represent straight lines, quadratic functions have a degree of 2 and form parabolic curves, cubic functions have a degree of 3 and create S-shaped curves, quartic functions have a degree of 4 and can have various shapes, and higher degree polynomial functions have degrees higher than 4, becoming increasingly complex.
Exploring Quadratic, Cubic, and Higher Degree Polynomials
Polynomials are algebraic expressions that have variables raised to whole number exponents. Quadratic, cubic, and higher degree polynomials are specific types of polynomials that have different degrees and shapes.
Quadratic polynomials are degree 2 polynomials, meaning that the highest power of the variable is 2. They can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic polynomial is a parabola, which can open upward or downward depending on the value of a. The vertex of the parabola is the minimum or maximum point of the function.
Cubic polynomials are degree 3 polynomials, meaning that the highest power of the variable is 3. They can be written in the form f(x) = ax^3 + bx^2 + cx + d, where a, b, c, and d are constants. The graph of a cubic polynomial can have various shapes, including “S” curves or multiple turning points. The cubic polynomial can have one, two, or three real roots.
Higher degree polynomials have degrees greater than 3. They can have complex graphs with multiple turning points, loops, and asymptotes. The behavior of the graph of a higher degree polynomial depends on the leading term, which is the term with the highest power of the variable.
In summary, quadratic, cubic, and higher degree polynomials are different types of polynomials that have different degrees and shapes. They can be represented by specific equations and have unique graph characteristics.
Characteristics of Polynomial Functions
A polynomial function is a mathematical function that is defined by a polynomial expression. Polynomial functions are characterized by several key properties that can help us understand and analyze the behavior of these functions.
One of the most important characteristics of polynomial functions is their degree. The degree of a polynomial function is determined by the highest power of the variable in the polynomial expression. For example, a polynomial of degree 3 would have a term with a variable raised to the power of 3.
The leading coefficient is another important characteristic of polynomial functions. It is the coefficient of the highest degree term in the polynomial expression. The leading coefficient can affect the overall shape and behavior of the polynomial function.
Polynomial functions can also have one or more roots or zeros. These are the values of the variable for which the polynomial function evaluates to zero. The number and nature of the roots of a polynomial function can provide insights into its behavior.
The end behavior of a polynomial function is determined by its degree and leading coefficient. For even-degree polynomials, the end behavior is typically the same on both ends, while for odd-degree polynomials, the end behavior can be different on each end. The leading coefficient determines whether the polynomial function rises or falls on each end.
In summary, the characteristics of polynomial functions, such as their degree, leading coefficient, roots, and end behavior, provide valuable information about the behavior and properties of these functions. By understanding these characteristics, we can analyze and solve problems involving polynomial functions more effectively.
Examining the Leading Coefficient, Degree, and End Behavior
A polynomial function is an algebraic expression that consists of one or more terms, with each term containing a constant coefficient multiplied by a variable raised to a non-negative integer power. The leading coefficient of a polynomial is the coefficient of the term with the highest degree. The degree of a polynomial is the highest power of the variable in any of its terms.
When analyzing a polynomial function, it is important to examine the leading coefficient, degree, and end behavior. The leading coefficient provides information about the direction in which the graph of the function opens. If the leading coefficient is positive, the graph opens upward. If the leading coefficient is negative, the graph opens downward.
The degree of a polynomial determines the number of possible turning points in the graph. For example, a polynomial of degree 0 (constant function) has no turning points, while a polynomial of degree 1 (linear function) has one turning point. Higher-degree polynomials can have multiple turning points.
The end behavior of a polynomial function describes how the function behaves as the input (x-values) approaches positive infinity or negative infinity. The end behavior is determined by the leading term of the polynomial, which has the largest influence on the overall behavior of the function. For example, if the leading term is an even-degree term with a positive leading coefficient, the function will approach positive infinity on both ends. If the leading term is an odd-degree term with a positive leading coefficient, the function will approach negative infinity on the left end and positive infinity on the right end.
Summary:
- A polynomial function consists of terms with constant coefficients multiplied by variables raised to non-negative integer powers.
- The leading coefficient is the coefficient of the term with the highest degree.
- The degree of a polynomial is the highest power of the variable in any of its terms.
- The leading coefficient and degree provide information about the direction and number of possible turning points in the graph of the function.
- The end behavior of a polynomial function is determined by the leading term and describes how the function behaves as the input approaches positive infinity or negative infinity.
Methods of Solving Polynomial Equations
Solving polynomial equations is an important skill in algebra, as it allows us to find the values of the variables that make the equation true. There are several different methods that can be used to solve polynomial equations, depending on the complexity of the equation and the desired level of accuracy.
Factoring
One of the most basic methods of solving polynomial equations is factoring. Factoring involves breaking down a polynomial equation into its simplest factors in order to find the values of the variables that make the equation true. This method is most commonly used for quadratic equations, where the polynomial is of the form ax^2 + bx + c = 0. By factoring the quadratic equation, we can find the values of x that make the equation true. However, factoring becomes increasingly difficult as the degree of the polynomial equation increases.
Graphing
Another method of solving polynomial equations is graphing. By plotting the polynomial equation on a graph and finding the x-intercepts (where the graph crosses the x-axis), we can determine the values of x that make the equation true. This method is particularly useful for higher degree polynomial equations, as it allows us to visualize the equation and find approximate solutions. However, graphing can be time-consuming and may not always provide an exact solution.
Numerical Methods

When exact solutions cannot be easily found using factoring or graphing, numerical methods can be used to find approximate solutions. Iterative methods, such as Newton’s method or the bisection method, involve repeatedly refining an initial estimate until a satisfactory solution is reached. These methods are often used in cases where the polynomial equation cannot be factored or graphed easily, such as with higher degree polynomials or equations with complex roots.
In conclusion, there are several methods available for solving polynomial equations, ranging from factoring to graphing to numerical methods. The choice of method will depend on the complexity of the equation and the desired level of accuracy. By understanding and utilizing these methods, we can efficiently solve polynomial equations and find the values of the variables that make the equation true.
Conclusion
Polynomial functions are an essential part of algebraic mathematics, and understanding how to factor, use the quadratic formula, and perform synthetic division is crucial for solving and analyzing these types of functions. By factoring a polynomial function, we can find the roots, or x-intercepts, which are valuable information for graphing and solving equations. The quadratic formula provides an alternative method for finding the roots of a quadratic equation, which is especially useful when a polynomial cannot be easily factored. Synthetic division allows for the division of polynomials, providing a way to simplify and solve polynomial equations quickly.
Overall, these techniques provide powerful tools for working with polynomial functions, allowing us to find roots, solve equations, and graph these functions accurately. By mastering these methods, we can enhance our understanding of polynomial functions and apply them to various real-world problems and mathematical concepts.