Understanding exponents and exponential functions is an essential part of mathematics and can be complex for many students. Unit 6 focuses on developing students’ knowledge and skills in this area, providing them with the tools they need to excel in algebra and beyond.
This answer key serves as a valuable resource for both students and teachers, providing comprehensive answers to all of the questions and exercises presented in Unit 6 of the textbook. It offers a step-by-step breakdown of each problem, allowing students to check their work and gauge their understanding of the material.
The key features of this answer key include clear explanations, detailed solutions, and helpful tips and strategies. It covers topics such as expressing numbers in scientific notation, using properties of exponents, solving exponential equations, and graphing exponential functions.
By utilizing this answer key, students can gain a deeper understanding of exponents and exponential functions, ultimately improving their overall math skills and achievement. The key allows them to quickly identify errors and learn from their mistakes, promoting a growth mindset and a more confident approach towards mathematics.
Understanding Unit 6 Exponents and Exponential Functions Answer Key
The Unit 6 Exponents and Exponential Functions Answer Key is an essential tool for understanding and mastering the concepts learned in this unit. This answer key provides detailed explanations and step-by-step solutions to the exercises and problems given in the textbook or practice workbook. It serves as a valuable resource for students to check their work, identify mistakes, and gain a deeper understanding of the material.
The Unit 6 Exponents and Exponential Functions Answer Key covers a wide range of topics, including properties of exponents, exponential growth and decay, scientific notation, and solving exponential equations. It provides clear explanations and examples to help students grasp the fundamental concepts and apply them to various problem-solving scenarios. The answer key also includes practice problems and additional exercises to reinforce the learning and allow students to further develop their skills.
One of the key benefits of using the Unit 6 Exponents and Exponential Functions Answer Key is that it allows students to self-assess their understanding of the material. By comparing their answers with the provided solutions, students can identify areas where they may need additional practice or further clarification. This self-assessment helps students become aware of their strengths and weaknesses and tailor their study and review accordingly.
In addition to helping students, the answer key is also a valuable resource for educators. Teachers can use it to verify the accuracy of their own solutions and to gain insights into common mistakes or misconceptions that students may have. By thoroughly understanding the answer key, educators can better explain the material and design effective lesson plans and activities to support student learning.
To sum up, the Unit 6 Exponents and Exponential Functions Answer Key is a valuable tool for both students and educators. It provides detailed explanations, step-by-step solutions, and additional practice problems to facilitate understanding and mastery of the concepts taught in this unit. By using the answer key effectively, students can improve their problem-solving skills and educators can enhance their teaching strategies to help students succeed in the subject.
Exploring the Basics of Exponents and Exponential Functions
Exponents and exponential functions are fundamental concepts in mathematics that play a significant role in various fields. Understanding these concepts is crucial for solving complex equations, analyzing data, and modeling phenomena in different disciplines such as finance, physics, and biology. In this article, we will explore the basics of exponents and exponential functions to develop a strong foundation for further mathematical studies.
An exponent is a shorthand notation used to represent repeated multiplication of a number by itself. It is written as a small superscript number placed to the upper right of a base number. For example, in the expression 2^3, the base is 2, and the exponent is 3. It indicates that we need to multiply 2 by itself three times, resulting in 2 x 2 x 2 = 8. Exponents enable us to express large or small numbers compactly and efficiently.
Key Concepts:
- Exponents can be positive, negative, or zero, representing different operations on the base number.
- Positive exponents indicate repeated multiplication, while negative exponents represent repeated division. For example, 2^(-3) is equivalent to 1/(2^3), which is 1/8.
- An exponent of zero results in the value of 1. For instance, 5^0 = 1.
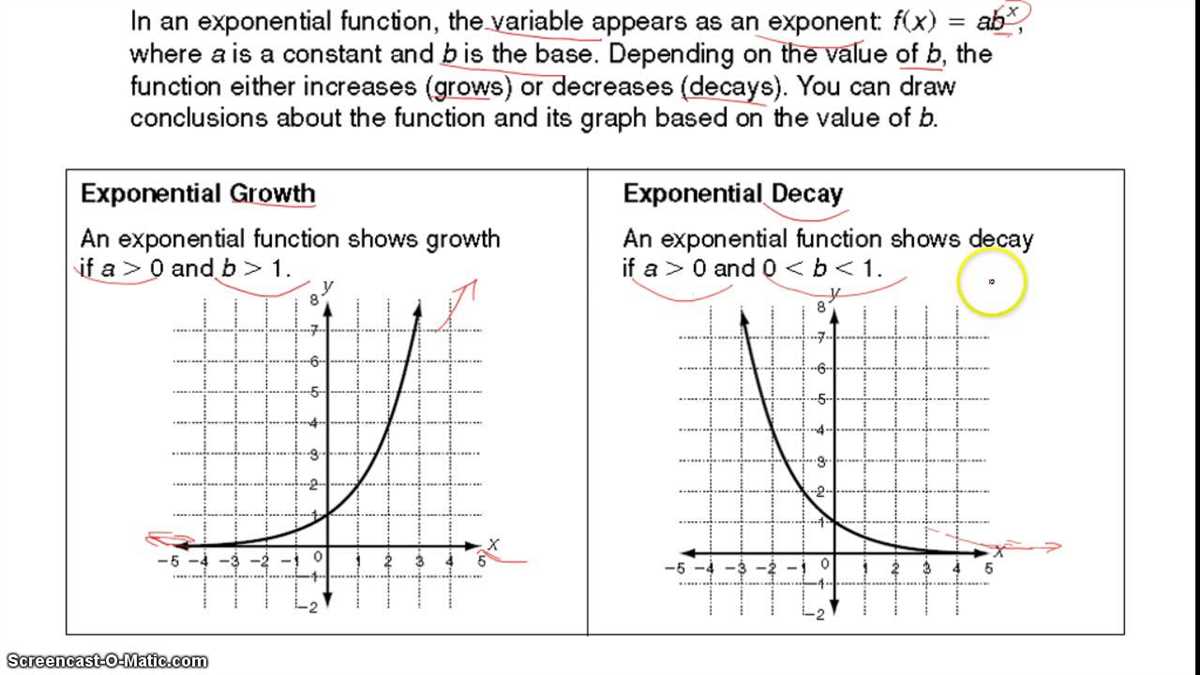
- Exponential functions involve the use of exponents to describe the growth or decay of a quantity over time. They are expressed in the form f(x) = a * b^x, where a is a constant and b is the base number.
- The base number in an exponential function determines its behavior. If the base is greater than 1, the function represents exponential growth. If the base is between 0 and 1, the function represents exponential decay.
Understanding the basics of exponents and exponential functions provides a solid foundation for more advanced mathematical concepts and applications. From calculating compound interest to analyzing population growth, these concepts are essential for tackling real-world problems and making informed decisions. By mastering exponents and exponential functions, individuals can build their mathematical competence and excel in various academic and professional fields.
Solving Problems with Exponents and Exponential Functions

Exponents and exponential functions play a crucial role in solving a wide range of mathematical problems. These concepts allow us to efficiently represent and manipulate large numbers and quantities that grow or decay at a certain rate.
One common application of exponents and exponential functions is in finance. When calculating compound interest, the amount of money in an account grows exponentially over time. By using the formula A = P(1 + r/n)^(nt), where A represents the final amount, P is the principal investment, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years, we can accurately determine the future value of an investment.
Another practical use of exponents and exponential functions is in population growth and decay. The exponential growth model, represented by the equation A(t) = A₀e^(kt), allows us to predict the future population of a species based on its current population and growth rate. This model is also applicable to other areas, such as the spread of diseases or the growth of bacteria in a petri dish.
When solving problems involving exponents and exponential functions, it is important to understand the properties and rules associated with these concepts. Some key concepts to remember include the multiplication rule of exponents, the power rule, and the relationship between exponential growth and decay. By applying these rules correctly, we can simplify complex equations and solve problems more efficiently.
In conclusion, exponents and exponential functions are powerful tools in solving a variety of mathematical problems. From calculating compound interest to predicting population growth, these concepts allow us to make accurate predictions and calculations in various fields. By understanding the fundamental principles and applying the relevant rules, we can confidently solve problems involving exponents and exponential functions.
Applying Exponents and Exponential Functions to Real-Life Scenarios
Exponents and exponential functions play a crucial role in solving real-life problems and understanding natural phenomena. Whether it’s calculating compound interest, modeling population growth, or analyzing radioactive decay, these mathematical concepts provide us with powerful tools to make sense of the world around us.
One practical application of exponents and exponential functions is in finance. For example, understanding compound interest allows us to calculate how our investments or loans will grow over time. By using the formula A = P(1 + r/n)^(nt), where A is the final amount, P is the principal (initial amount), r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years, we can determine how our money will grow or accumulate debt.
In the field of biology, exponential growth and decay are frequently observed. For instance, population growth can be modeled using the formula P(t) = P0 * e^(rt), where P(t) represents the population at time t, P0 is the initial population, e is Euler’s number (approximately 2.71828), and r is the growth rate. This formula allows us to predict how a population will change over time and understand the factors contributing to its growth or decline.
Another real-life scenario where exponents and exponential functions are applied is in radioactive decay. The half-life of a radioactive substance determines how long it takes for half of its atoms to decay. This can be calculated using the formula N(t) = N0 * (1/2)^(t/h), where N(t) represents the number of remaining atoms at time t, N0 is the initial number of atoms, t is the time elapsed, and h is the half-life. This formula is used to estimate the remaining radioactivity of substances and is essential in fields such as nuclear science and medicine.
Overall, exponents and exponential functions are essential tools for understanding and solving real-life problems. By applying these concepts to various scenarios, we can make informed decisions, predict outcomes, and unravel the mysteries of the natural world.
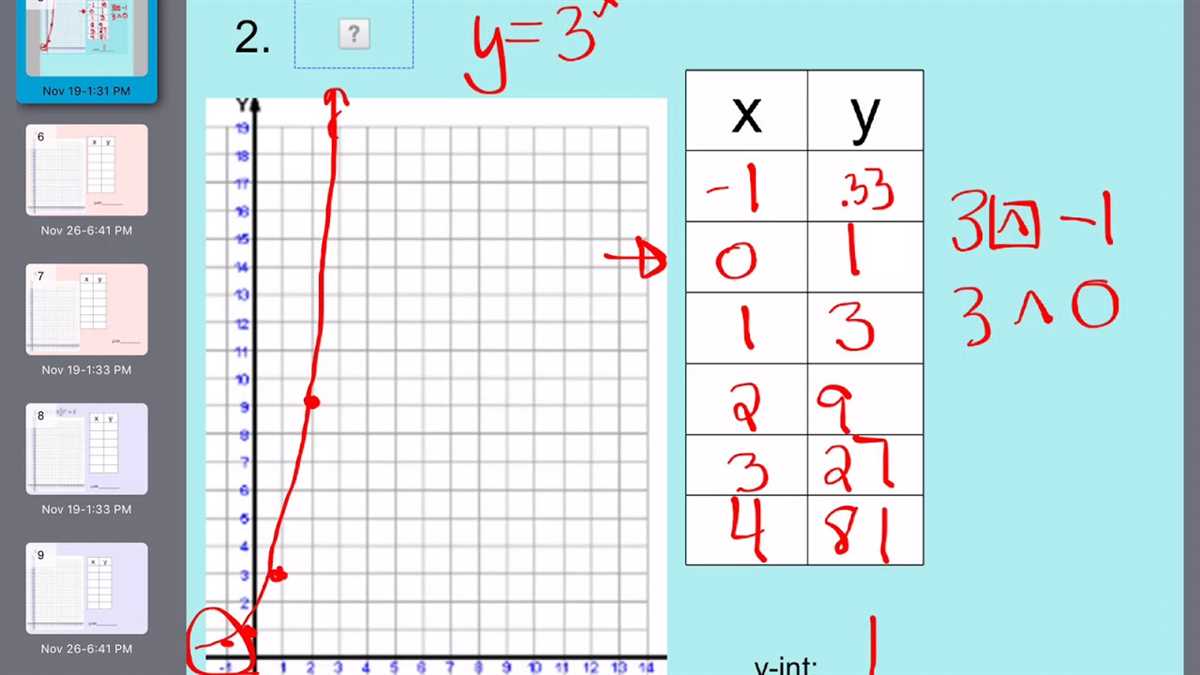
Analyzing Graphs and Patterns of Exponential Functions
In the study of exponential functions, it is important to analyze their graphs and patterns in order to understand their behavior and make predictions. These functions have a unique property where the output values increase or decrease at an exponential rate, rather than a linear or constant rate.
One way to analyze the graph of an exponential function is to look at its key features, such as the y-intercept, the slope, and any horizontal or vertical asymptotes. The y-intercept is the point where the graph crosses the y-axis, and it can provide information about the initial value or starting point of the function. The slope of an exponential function graph represents the rate of change, and it can indicate whether the function is increasing or decreasing. Horizontal asymptotes are horizontal lines that the graph gets closer to as x approaches positive or negative infinity, and they can help determine the long-term behavior of the function.
Another important aspect of analyzing exponential functions is identifying the patterns in their graphs. Exponential functions often exhibit growth or decay patterns that can be represented by an algebraic formula. For example, if the graph of an exponential function increases rapidly at first and then levels off, it may indicate exponential growth with a base greater than 1. On the other hand, if the graph decreases rapidly at first and then levels off, it may indicate exponential decay with a base between 0 and 1.
By analyzing the graphs and patterns of exponential functions, we can gain a deeper understanding of their behavior and make predictions about their future values. This knowledge is crucial in various fields such as finance, economics, and biology, where exponential growth or decay is often observed.
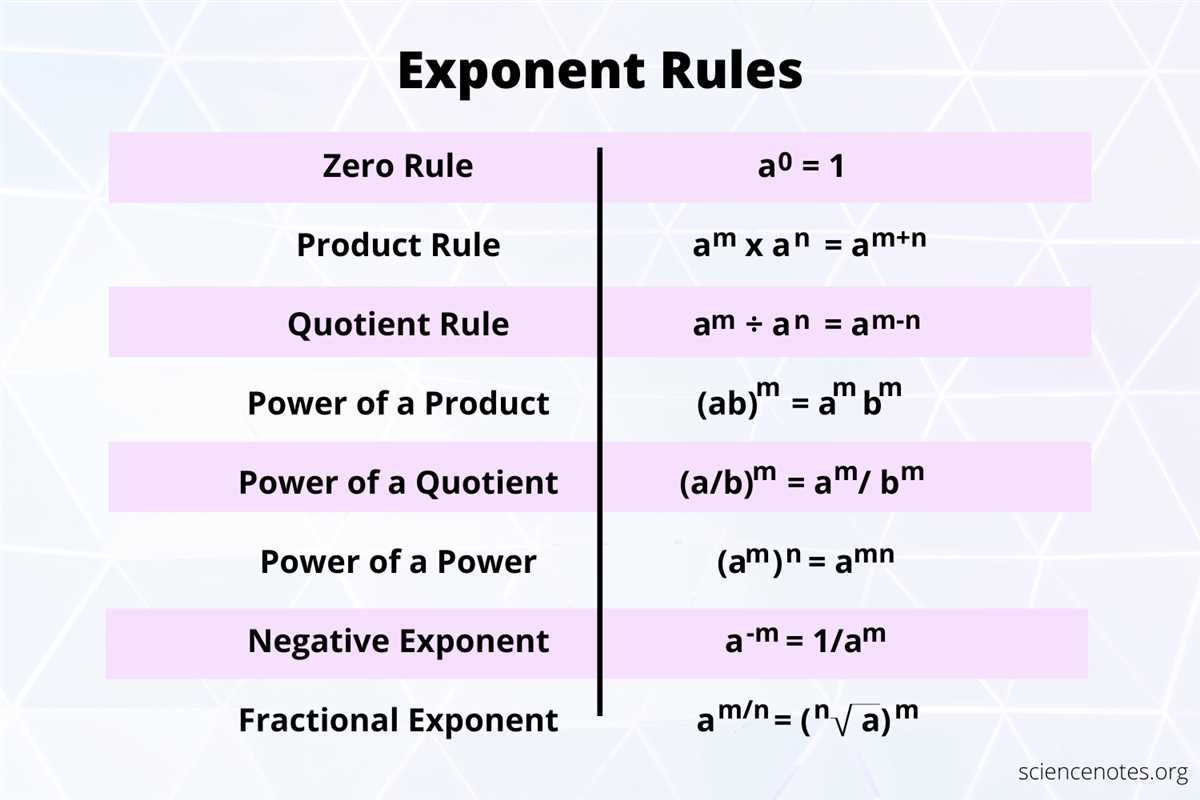
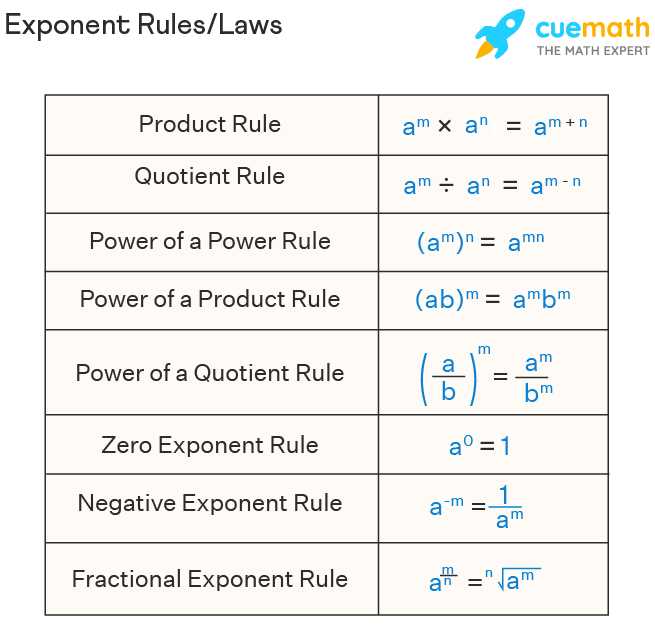
Understanding Properties and Rules of Exponents
The properties and rules of exponents are fundamental concepts in mathematics that allow us to simplify and manipulate exponential expressions. By understanding these properties, we can solve complex equations, simplify expressions, and work with exponential functions more effectively.
One of the most basic properties of exponents is the power of a power rule. This rule states that when a base is raised to an exponent, and that result is raised to another exponent, we can multiply the exponents together. For example, if we have (a^m)^n, we can simplify it to a^(m*n). This property allows us to simplify expressions and work with higher powers more easily.
Another important property is the product rule of exponents. This rule states that when multiplying two exponentials with the same base, we can add the exponents together. For instance, if we have a^m * a^n, we can simplify it to a^(m+n). This property is especially useful when dealing with multiplication or dividing exponential terms.
Furthermore, the quotient rule of exponents is similar to the product rule, but it applies to division. This rule states that when dividing two exponential terms with the same base, we can subtract the exponents. For example, if we have a^m / a^n, we can simplify it to a^(m-n). This property allows us to simplify expressions involving division and fractions with exponential terms.
In summary, understanding the properties and rules of exponents is crucial in simplifying expressions, solving equations, and working with exponential functions. These rules, such as the power of a power rule, the product rule, and the quotient rule, allow us to manipulate and simplify exponential expressions, making them more manageable and easier to work with.
Reviewing and Practicing Exponents and Exponential Functions
In this article, we have explored various concepts and applications of exponents and exponential functions. We began by defining exponents and reviewing the basic rules for working with them, including multiplying and dividing with exponents and raising a power to a power. We also discussed the properties of exponential functions and how to graph them.
Throughout the article, we provided examples and practice problems to help reinforce the concepts and techniques. By practicing these problems, we can improve our understanding and proficiency in working with exponents and exponential functions.
Key takeaways from this review include:
- Exponents represent repeated multiplication, and they have certain rules for combining and manipulating them.
- Exponential functions have a base raised to a variable exponent, and they can be graphed to show exponential growth or decay.
- Exponential functions can be used to model real-world phenomena, such as population growth or compound interest.
- By practicing problems and exercises, we can improve our skills in working with exponents and exponential functions.
Overall, understanding exponents and exponential functions is important for various calculations and real-world applications. By reviewing and practicing these concepts, we can develop a strong foundation in this area of mathematics.