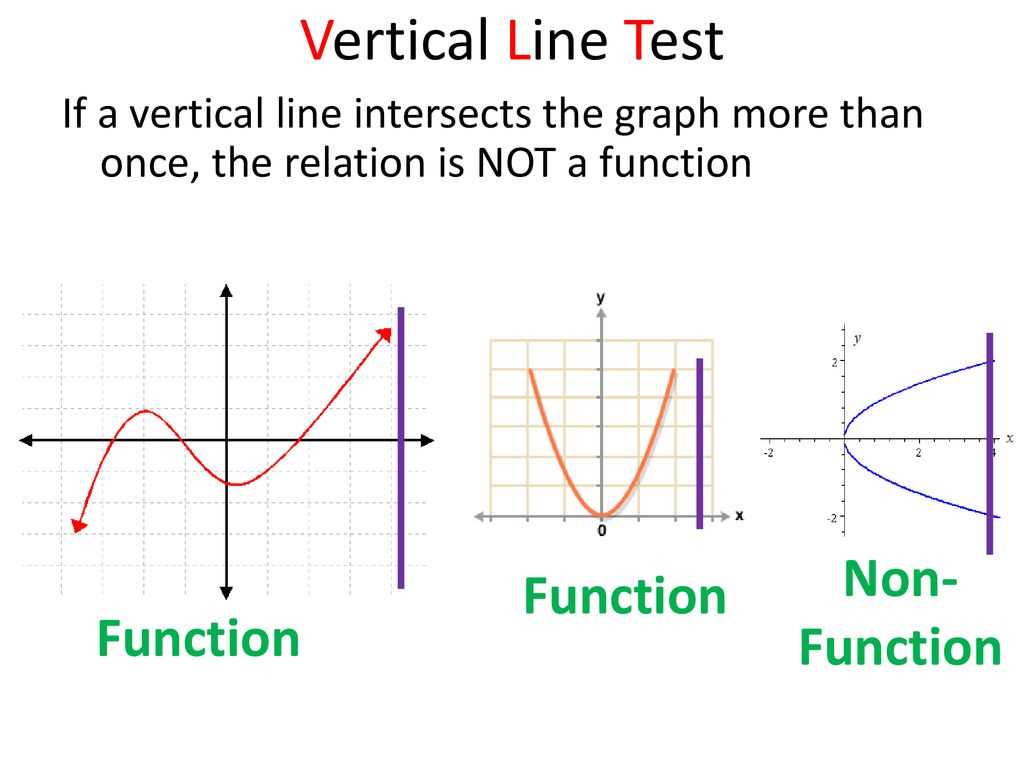
In mathematics, certain methods are used to assess the behavior of shapes and their ability to represent functions. This process involves testing whether a curve or figure intersects a series of imagined lines drawn through the plane. The purpose of this evaluation is to determine if the graph represents a specific kind of relationship or function.
Purpose of the Evaluation Method
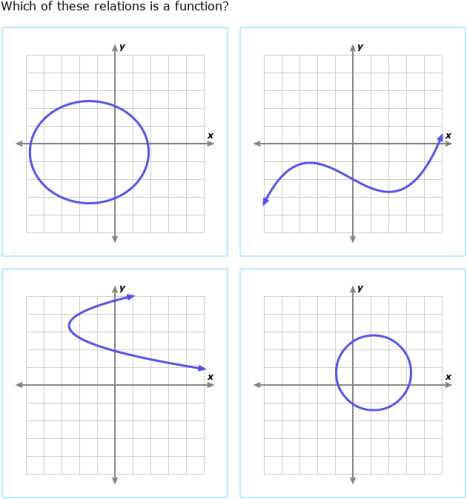
This approach helps determine if a given figure adheres to the principles of being a function. A function, in this case, is a relationship where every input has a single output. Using the described method, we can verify whether a shape or curve satisfies this condition.
How It Works
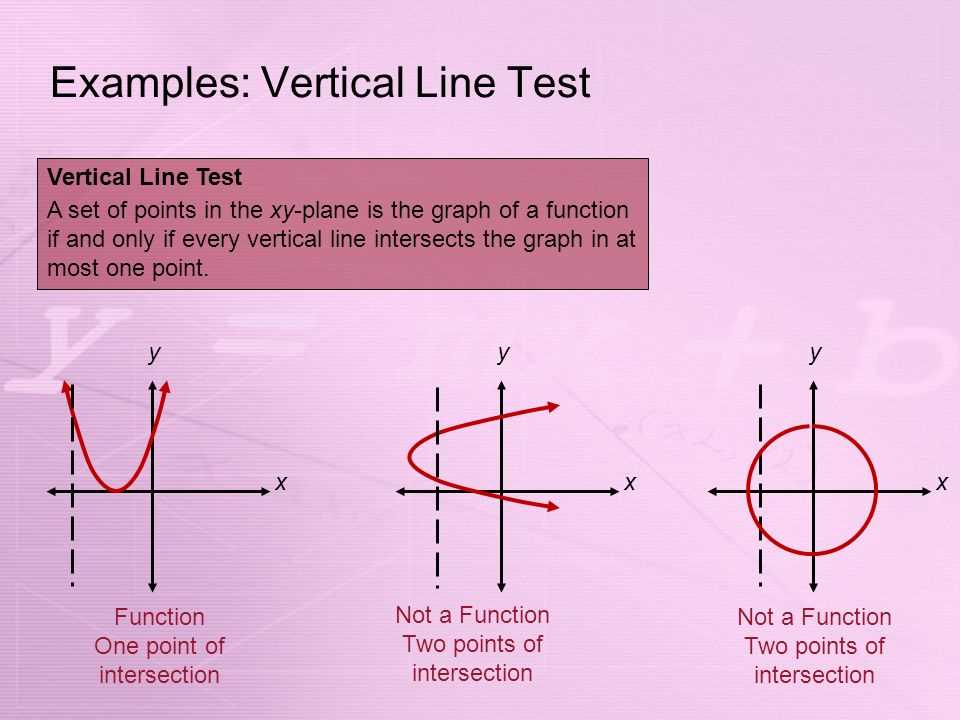
By drawing lines vertically through a graph, we can observe whether these lines intersect the figure at more than one point. If they do, the graph does not represent a function, as it fails the basic principle of assigning one output to each input.
Common Misunderstandings
Some might think that the graphical evaluation applies only to specific types of curves. However, it is a general method that works for various shapes, not limited to simple lines but also to more complex figures.
Practical Examples
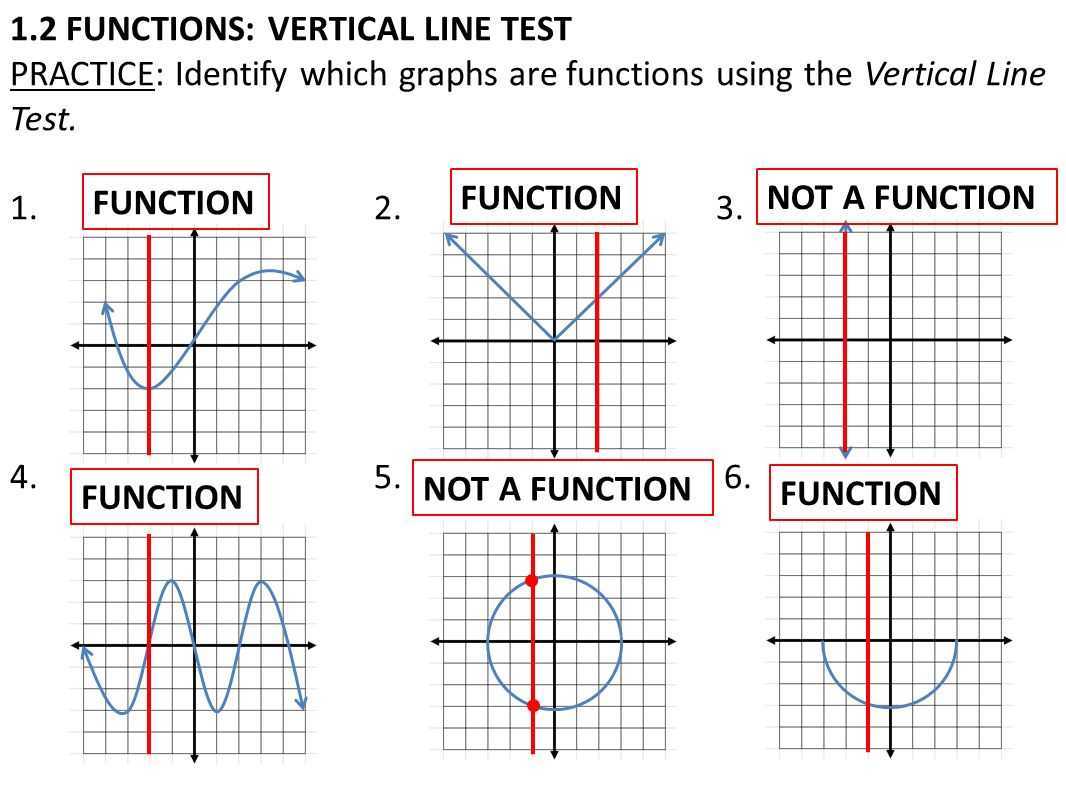
- For a straight line, the evaluation confirms that it represents a function, as no vertical line intersects it more than once.
- A circle, on the other hand, will fail the evaluation, as it is intersected by vertical lines at two points.
Importance in Mathematics
This method serves as a foundational tool in understanding functions, especially in calculus and algebra. It provides a quick, visual check for determining whether a graph can represent a function, simplifying complex analysis for students and professionals alike.
Understanding the Concept of Graph Evaluation
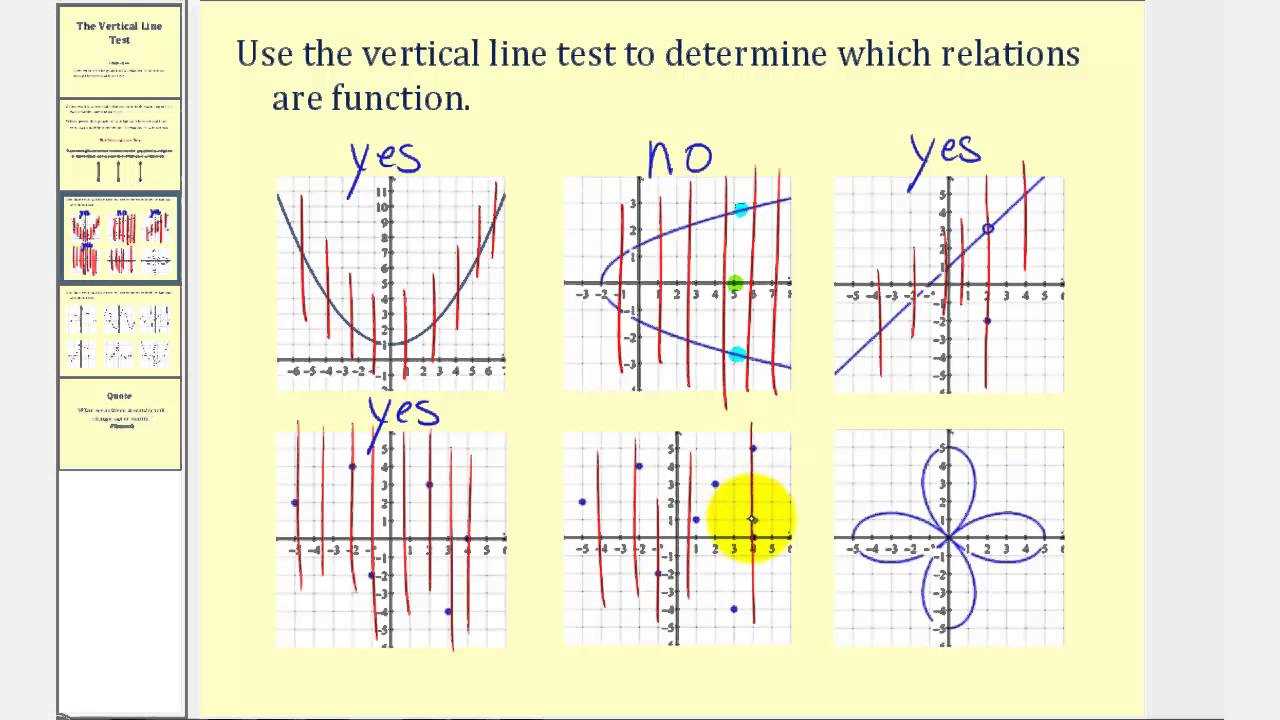
In mathematics, one important process is assessing whether a curve or figure represents a valid relationship. This evaluation helps determine if the graph of a function meets specific criteria, ensuring it is a valid representation of a mathematical function.
Steps for Performing the Evaluation
To perform the graphical evaluation, draw multiple lines through the graph at different positions. The purpose is to check if any of these lines intersect the figure at more than one point. If any line crosses the graph more than once, the figure does not represent a function.
Identifying Common Errors in the Process
A frequent mistake during this process is misidentifying intersections. It is essential to carefully observe each line’s path through the figure to avoid errors. Overlooking multiple intersections may lead to incorrect conclusions about whether the graph meets the criteria.
Importance of the Graphical Evaluation
This method is vital for distinguishing between different types of relationships, such as functions and non-functions. It provides a quick and reliable way to assess whether a given graph adheres to the fundamental definition of a function.
Real-World Uses of the Evaluation
In various fields, such as economics, physics, and engineering, this evaluation helps to confirm if data sets or relationships follow consistent patterns. Whether analyzing market trends or modeling physical systems, the ability to check if a relationship is a function is crucial for accurate predictions and analyses.
How to Interpret the Evaluation Results
When performing the evaluation, if a graph passes, it confirms that the relationship depicted adheres to the one-to-one correspondence principle. On the other hand, failing the evaluation means that the graph represents a more complex relationship, which may require a different approach for analysis.
Application in Geometry
This evaluation is often applied in geometric contexts, especially when studying curves and surfaces. It helps to quickly determine the nature of geometric shapes and whether they represent valid functions, simplifying geometric proofs and problem-solving.