Worksheet piecewise functions answer key is available for download and can be presented in a variety of formats. It consists of questions and answers on piecewise functions which many students generally find challenging to understand. This answer key provides step-by-step solutions for all the questions presented in the worksheet. It is a valuable resource for both teachers and students to review and practice piecewise functions.
Piecewise functions are mathematical functions that are defined by several different expressions or formulas in different intervals or subdomains of the input. The purpose is to provide a specific output value based on the given input value, depending on which interval or subdomain the input falls into. In other words, piecewise functions can have different rules for different portions of their domains.
The worksheet on piecewise functions typically includes questions that require students to find the value of a given piecewise function for a specific input or interval, graph a piecewise function, determine the domain and range of a piecewise function, and solve equations involving piecewise functions. These questions are designed to test the students’ understanding of the concept and their ability to apply the rules of piecewise functions.
By using the answer key to the worksheet on piecewise functions, teachers can easily check the accuracy of their students’ work and provide feedback or additional guidance. Students can also use the answer key to self-assess their work and identify any mistakes or areas of weakness that need improvement. Additionally, the answer key can serve as a study guide for students to review before quizzes or exams on piecewise functions.
Worksheet Piecewise Functions Answer Key
When working with piecewise functions, it is important to correctly identify the different pieces and their corresponding domains. This answer key provides the solutions to the worksheet questions, helping students check their work and verify the accuracy of their answers.
Here are the answers to the questions on the worksheet:
- Question 1: Determine the value of the function f(x) when x = 2.
- Answer 1: The value of f(x) when x = 2 is 4.
- Question 2: Find the domain of the piecewise function g(x) = |x + 3|.
- Answer 2: The domain of the piecewise function g(x) = |x + 3| is all real numbers.
- Question 3: Evaluate the piecewise function h(x) = {3x – 5, x ≥ 0; -2x + 1, x < 0} when x = -2.
- Answer 3: The value of h(x) when x = -2 is 5.
By referencing this answer key, students can determine if their answers match the correct solutions and can clarify any misunderstandings they may have had while completing the worksheet. It also serves as a useful tool for teachers when grading and providing feedback to their students.
Overview of Piecewise Functions
A piecewise function is a function that is defined by two or more separate expressions, each of which is applicable to a certain interval or set of intervals. In other words, a piecewise function can be thought of as a function that has different rules or formulas for different parts of its input.
Piecewise functions are commonly used in mathematics and other fields to represent situations where different rules apply in different situations. For example, in economics, piecewise functions can be used to model tax rates, where different rates apply to different income brackets. In physics, piecewise functions can be used to model the motion of an object under different conditions, such as when it is moving at a constant velocity versus when it is accelerating or decelerating.
A piecewise function can be represented using a combination of equations, inequalities, and logical operators. Each equation or inequality represents a rule that is valid for a specific interval or set of intervals. The rules are typically separated by a comma or a vertical bar symbol, and the intervals are specified within parentheses or brackets.
When working with piecewise functions, it is important to identify the domain of the function, which is the set of all possible input values. The domain is determined by the intervals specified in the piecewise function. Additionally, piecewise functions can be graphed to visualize the different parts and their corresponding rules. Graphing piecewise functions can help in analyzing and understanding their behavior and characteristics.
How to Determine the Domain of Piecewise Functions

When dealing with piecewise functions, the domain refers to the set of all possible input values for which the function is defined. It’s important to find the domain of a piecewise function in order to understand the range of values that can be used as input. Let’s explore the steps to determine the domain of piecewise functions:
Step 1: Start by examining the different pieces of the piecewise function. Identify the conditions or restrictions for each piece. These conditions could be expressed as equations, inequalities, or specific values.
Step 2: Analyze the domain for each piece separately. Determine the set of inputs that satisfy the conditions or restrictions for that specific piece. This may involve solving equations or inequalities, or identifying specific values that are included or excluded.
Step 3: Combine the domains of all the pieces. Take the intersection of the individual domains to find the common set of inputs that satisfy all the conditions or restrictions for the entire piecewise function. This will give you the overall domain of the function.
In some cases, the domain of a piecewise function may include all real numbers. However, there may be situations where certain values are excluded due to restrictions in the function. It’s important to carefully analyze the conditions or restrictions for each piece and consider any potential exclusions.
Example:
| Piece | Condition | Domain |
|---|---|---|
| Piece 1 | x < 0 | (-∞, 0) |
| Piece 2 | x ≥ 0 | [0, +∞) |
In this example, the domain of the piecewise function consists of all real numbers less than 0 (for Piece 1) and all real numbers greater than or equal to 0 (for Piece 2).
By following these steps, you can determine the domain of piecewise functions and gain a better understanding of the possible input values for which the function is defined.
Graphing Piecewise Functions: Step-by-Step Guide
Graphing piecewise functions can be a bit challenging, but with a step-by-step guide, it becomes much easier. Piecewise functions are defined by different rules or equations for different intervals. Each interval has its own set of conditions and equations, making the overall graph a combination of different segments.
Step 1: Identify the Intervals
The first step in graphing a piecewise function is to identify the intervals defined by the different conditions. These conditions are typically given in the form of ranges or specific values for the independent variable. Each interval will have its own equation or rule.
Step 2: Graph Each Interval
Once the intervals are identified, graph each interval separately according to its corresponding equation or rule. Start with the first interval and plot the points based on the equation. Connect the plotted points to form a segment. Repeat this process for each interval, making sure to follow the correct equation or rule for that specific interval.
Step 3: Connect the Segments
After graphing each interval separately, it’s time to connect the segments together to form the complete graph. Look for any discontinuities or points where the segments meet but do not connect smoothly. These points may be indicated by open circles or dots. Connect the segments, making sure to include any discontinuities as indicated.
Step 4: Label the Graph
Finally, label the graph with any important information such as the domain, range, and any other relevant details. This will help in understanding and interpreting the graph.
By following these steps, you can successfully graph piecewise functions and gain a better understanding of their behavior and characteristics. Practice with different examples to improve your graphing skills and become more familiar with piecewise functions.
Finding the Range of Piecewise Functions
A piecewise function is a mathematical function that is defined by different expressions or formulas for different intervals or sets of input values. When working with piecewise functions, one important task is to find the range of the function, which represents all possible output values.
To find the range of a piecewise function, we need to consider the range of each individual expression or formula that makes up the function. For each interval or set of input values, we evaluate the expression and determine the range of the corresponding output values.
To simplify the process of finding the range, it is important to identify the boundaries or transition points between different intervals or sets of input values. These boundaries are the points where the function changes its expression or formula. By determining the output values at these boundaries, we can establish the range of the piecewise function.
When dealing with piecewise functions that contain functions such as absolute value, square root, or logarithm, it is important to consider the domain restrictions. These restrictions may result in a limited range for the function, as some output values may not be defined for certain input values. It is crucial to analyze the domain and range restrictions of each expression within the piecewise function to accurately determine the overall range.
In summary, finding the range of a piecewise function involves evaluating each expression or formula in different intervals or sets of input values, considering the boundaries between intervals, and taking into account any domain restrictions. By following these steps, we can accurately determine the range of a piecewise function.
Evaluating Piecewise Functions: Examples and Solutions
When working with piecewise functions, it’s important to understand how to evaluate them. Piecewise functions are functions that are defined by different rules or formulas for different intervals of the input variable. This allows the function to have different behaviors or outputs depending on the value of the input.
To evaluate a piecewise function, you need to determine which rule or formula applies to the given input. This is typically done by checking the interval in which the input falls and applying the corresponding rule. Let’s look at some examples to see how this works in practice.
Example 1:
Consider the piecewise function f(x) defined as:
f(x) = 2x if x < 3, = x^2 if x ≥ 3.
For x = 2, we are in the first interval where the rule is f(x) = 2x. Therefore, we can evaluate the function by substituting x = 2 into this rule:
f(2) = 2(2) = 4.
So, f(2) is equal to 4.
Example 2:
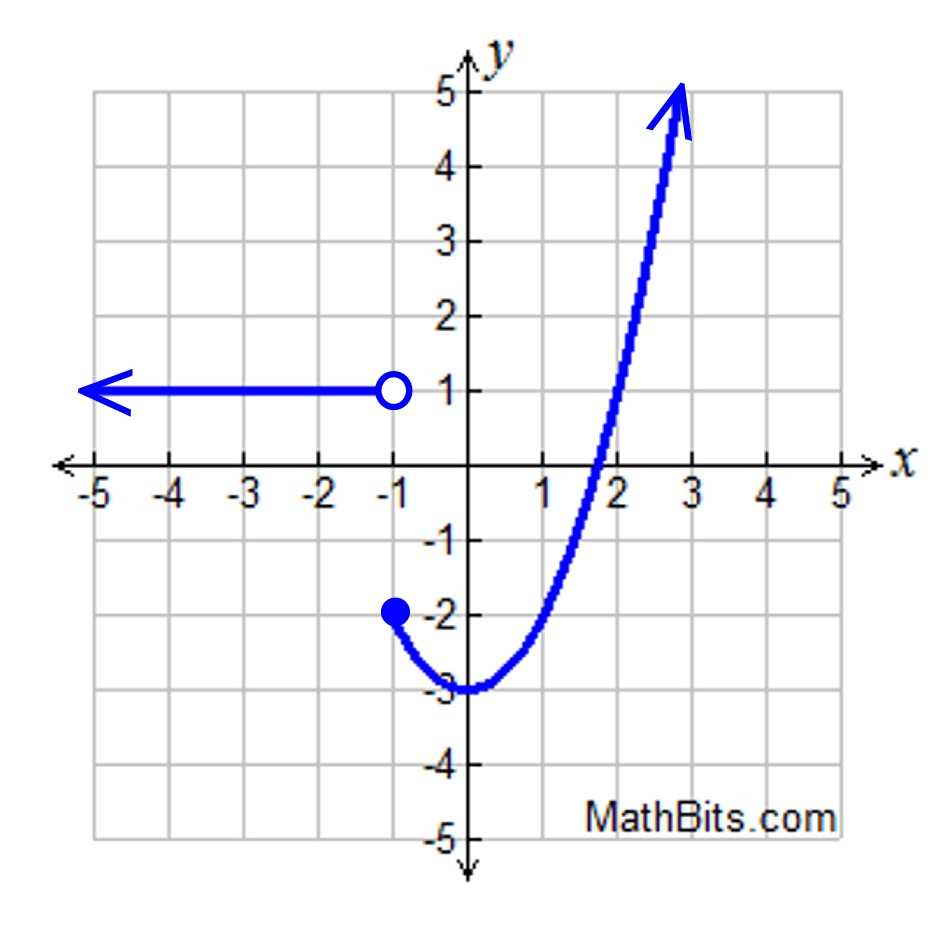
Now let’s consider the piecewise function g(x) defined as:
g(x) = 3x + 1 if x < -2, = x - 2 if -2 ≤ x ≤ 2, = x^2 if x > 2.
For x = 1, we are in the second interval where the rule is g(x) = x – 2. Therefore, we can evaluate the function by substituting x = 1 into this rule:
g(1) = 1 - 2 = -1.
So, g(1) is equal to -1.
In summary, when evaluating piecewise functions, it’s essential to determine the interval in which the input falls and apply the corresponding rule. This allows us to find the correct output or value of the function for a given input.
Using Piecewise Functions in Real-Life Scenarios
Piecewise functions are not just a concept learned in math class; they have practical applications in various real-life scenarios. By understanding and using piecewise functions, we can model and solve problems that involve different conditions or scenarios.
One common application of piecewise functions is in the field of finance. For example, in personal finance, we can use piecewise functions to model tax rates. Tax rates often change at different income levels, and we can represent this using a piecewise function. By using this model, we can calculate the exact amount of taxes owed based on income levels.
Another application of piecewise functions is in the field of physics. In physics, many phenomena have different rules or conditions depending on specific factors. For instance, the motion of an object may be described differently depending on whether it is in free fall or in contact with a surface. By using piecewise functions, we can accurately model and analyze these complex scenarios.
Overall, piecewise functions are a powerful tool in mathematics with practical applications in various fields. They allow us to represent real-life scenarios with different conditions or rules, enabling us to solve problems and make predictions. By mastering the concept of piecewise functions, we can better understand and navigate the complexities of the world around us.