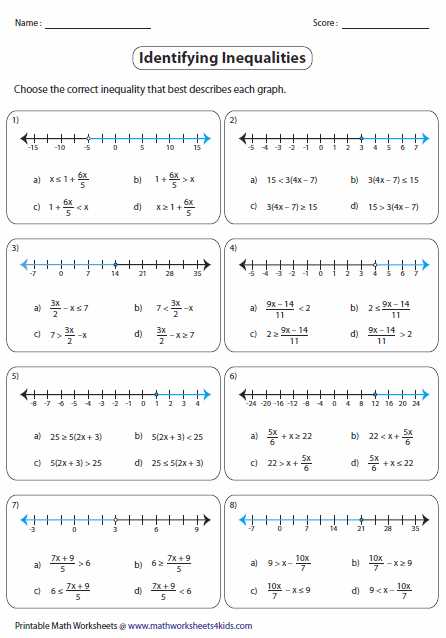
When learning how to write inequalities, it is essential to have practice problems to reinforce the concepts and ensure understanding. That’s where a writing inequalities worksheet comes in handy. These worksheets provide students with a range of inequalities to solve, allowing them to practice their skills and check their answers for accuracy.
A writing inequalities worksheet typically includes a set of inequalities or word problems that require students to write the corresponding mathematical expressions. Students will need to determine the appropriate inequality symbol (< for “less than,” > for “greater than,” ≤ for “less than or equal to,” or ≥ for “greater than or equal to”) and write the equation accordingly.
Students can work through the problems on the worksheet at their own pace, using their understanding of inequalities to correctly express the given information. Once they have completed the worksheet, they can consult the provided answer key to check their work and ensure they have correctly written the inequalities.
Writing inequalities worksheets are a valuable tool for reinforcing and assessing students’ knowledge of inequalities. By working through a variety of problems and checking their answers, students can cement their understanding of how to express inequalities mathematically. Whether used as individual practice or as a classroom assignment, these worksheets provide students with the opportunity to develop and refine their skills in writing inequalities.
Writing Inequalities Worksheet Answers
Writing inequalities is an important skill in algebraic equations. It enables us to represent mathematical relationships using symbols and compare quantities. A writing inequalities worksheet provides the opportunity to practice this skill and assess understanding. In this article, we will explore a few sample answers to such a worksheet.
Problem 1: Write an inequality to represent the statement “The temperature is greater than 80 degrees Fahrenheit.”
The correct answer to this problem would be: T > 80, where T represents the temperature in degrees Fahrenheit.
Problem 2: Write an inequality to represent the statement “The cost of a concert ticket is no more than $100.”
The correct answer to this problem would be: C ≤ 100, where C represents the cost of a concert ticket in dollars.
Problem 3: Write an inequality to represent the statement “The number of students in a class is at least 25.”
The correct answer to this problem would be: S ≥ 25, where S represents the number of students in the class.
These are just a few examples of how to write inequalities based on given statements. Writing inequalities enables us to translate real-life situations into mathematical language and solve problems in a precise and concise manner.
Understanding Inequalities

An inequality is a mathematical statement that compares the values of two expressions using one of the symbols < (less than), > (greater than), ≤ (less than or equal to), or ≥ (greater than or equal to). Inequalities can be represented graphically on a number line, or solved algebraically to determine the range of possible values for a variable.
Inequalities are used to express relationships between quantities that are not necessarily equal. They are commonly used in real-life situations to represent constraints or conditions. For example, an inequality can be used to represent the minimum age requirement for a movie ticket, or the maximum weight limit for an airplane.
When solving inequalities, it is important to remember the rules of inequality operations. Just like when solving equations, you can perform addition, subtraction, multiplication, and division on both sides of an inequality. However, there is one key difference: if you multiply or divide by a negative number, you must reverse the direction of the inequality symbol. This is because multiplying or dividing by a negative number will change the order of the numbers being compared.
To practice understanding and solving inequalities, you can use worksheets that provide a variety of inequality problems. These worksheets often include word problems, where you need to translate the given information into an inequality and solve for the unknown variable. By practicing with these worksheets and understanding the rules of inequality operations, you can develop a strong foundation in solving inequalities and apply this knowledge to real-life situations.
Writing Inequalities in One Variable
When working with inequalities in math, we often need to express relationships between numbers using symbols like < (less than), > (greater than), ≤ (less than or equal to), or ≥ (greater than or equal to). These symbols help us represent the limitations or conditions for a given situation. When writing inequalities in one variable, we focus on expressing these conditions using a combination of numbers, variables, and the appropriate inequality symbol.
For example:
- If we have a number line and need to represent that a number is less than 5, we would write the inequality as x < 5. Here, x represents any number less than 5. The open point at 5 on the number line indicates that 5 is not included in the solution set.
- To represent that a number is greater than or equal to 2, we would write the inequality as x ≥ 2. Here, x represents any number greater than or equal to 2. The closed point at 2 on the number line indicates that 2 is included in the solution set.
- If we need to represent that a number is between two values, such as between 1 and 6, we would write the inequality as 1 < x < 6. Here, x represents any number greater than 1 and less than 6. The open points at 1 and 6 on the number line indicate that these values are not included in the solution set.
Overall, when writing inequalities in one variable, it is important to clearly define the variable, choose the appropriate inequality symbol, and consider whether the values at the endpoints are included or not. This allows us to accurately represent relationships and conditions within a mathematical problem.
Graphing One-Variable Inequalities

Graphing one-variable inequalities involves representing the solutions to the inequality on a number line. This allows us to visually see the range of values that satisfy the inequality. We can determine which values are included or excluded from the solution set by analyzing the inequality symbols.
When graphing a greater than or less than inequality, such as x > 3 or x < -2, we use an open circle to represent the endpoint. This means that the value at that point is not included in the solution set. We then shade the region either to the right or left of the open circle to represent all the values that satisfy the inequality.
For inequalities involving greater than or equal to or less than or equal to, such as x ≥ -1 or x ≤ 5, we use a closed circle to represent the endpoint. This indicates that the value at that point is included in the solution set. We then shade the region to the right or left of the closed circle, depending on the direction of the inequality symbol, to represent all the values that satisfy the inequality.
It is important to note that when graphing inequalities on a number line, we are only representing the solutions as a visual aid. The actual solution set is typically written in interval notation or set-builder notation.
- Example 1: Graph the inequality x > 3
- Example 2: Graph the inequality x ≤ -2
- Example 3: Graph the inequality x ≥ 0
Writing Compound Inequalities
A compound inequality is an inequality that combines two or more simple inequalities using the words “and” or “or”. These compound inequalities can be represented using symbols and expressions to convey certain relationships between variables or numbers.
When writing compound inequalities, it’s important to first understand the meaning of the words “and” and “or” in mathematical terms. “And” means that both conditions must be true, while “or” means that at least one of the conditions must be true.
For example, the compound inequality “x > 4 and x < 8" means that the variable x must be greater than 4 and less than 8 at the same time. On the other hand, the compound inequality "x > 4 or x < 8" means that the variable x can be either greater than 4 or less than 8 (or both).
Compound inequalities can also involve variables and constants, such as “2x + 3 < 10 and x > 2″. In this case, the inequality represents two conditions: the expression 2x + 3 must be less than 10, and the variable x must be greater than 2.
- To write compound inequalities, follow these steps:
- Identify the conditions or constraints given in the problem.
- Translate each condition into a simple inequality statement.
- Join the simple inequalities using the words “and” or “or”.
- Choose the appropriate inequality symbols to represent the compound inequality.
It is important to note that when writing compound inequalities, the direction of the inequality symbol may change depending on whether “and” or “or” is used. For “and”, the inequality symbol remains the same, while for “or”, the inequality symbol changes to represent the union of the two conditions.
Overall, writing compound inequalities requires an understanding of basic inequality concepts and the ability to combine multiple conditions using appropriate symbols and expressions. By mastering this skill, students can solve more complex inequalities and apply them to real-world situations.
Solving Inequalities with Absolute Value

In mathematics, absolute value represents the distance between a number and zero on the number line. When dealing with inequalities involving absolute value, we have to consider both the positive and negative solutions. Solving inequalities with absolute value can be done by considering two separate cases: when the expression inside the absolute value is positive and when it is negative.
To solve inequalities with absolute value, we first isolate the absolute value expression by removing any other terms on the same side of the inequality. Then, we rewrite the inequality as two separate inequalities, one with a positive expression inside the absolute value and one with a negative expression inside the absolute value. We then solve both inequalities separately, obtaining two sets of solutions.
After finding the solutions for each case, we combine them to form the final solution. If the original inequality involves “less than” or “greater than” signs, the solution will be the union of the solutions from both cases. However, if the inequality involves “less than or equal to” or “greater than or equal to” signs, we have to consider the intersection of the solutions from both cases.
In summary, solving inequalities with absolute value requires considering both the positive and negative solutions. By isolating the absolute value expression, rewriting it as two separate inequalities, and solving each case individually, we can find the solutions to the original inequality. It is important to carefully consider the signs and symbols involved in the inequality to accurately determine the final solution.
Real-Life Applications of Inequalities

Inequalities can be found in many real-life situations, where they help to model and solve problems related to quantities that are not equal. In this section, we will explore some common examples of how inequalities are used in various fields.
1. Finance
In the field of finance, inequalities are commonly used to model and solve problems related to budgeting, investments, and loans. For example, when determining how much money can be borrowed for a loan, an inequality equation is often used to ensure that the borrower’s income is sufficient to cover the loan payments.
Investors also use inequalities to analyze the potential return on investments and make decisions based on risk. By comparing the expected return with the risk associated with an investment, investors can determine whether the investment is worth pursuing.
2. Transportation
Inequalities are also used in transportation planning and logistics. For instance, when deciding how many buses or trains are needed for a specific route, transportation planners use inequalities to ensure that the demand for transportation services can be met.
Additionally, inequalities are used to model and solve traffic flow problems. By considering factors such as the number of vehicles on the road, the speed limits, and the road capacity, transportation engineers can determine if a road or intersection is operating efficiently or if improvements are needed.
3. Health and Medicine
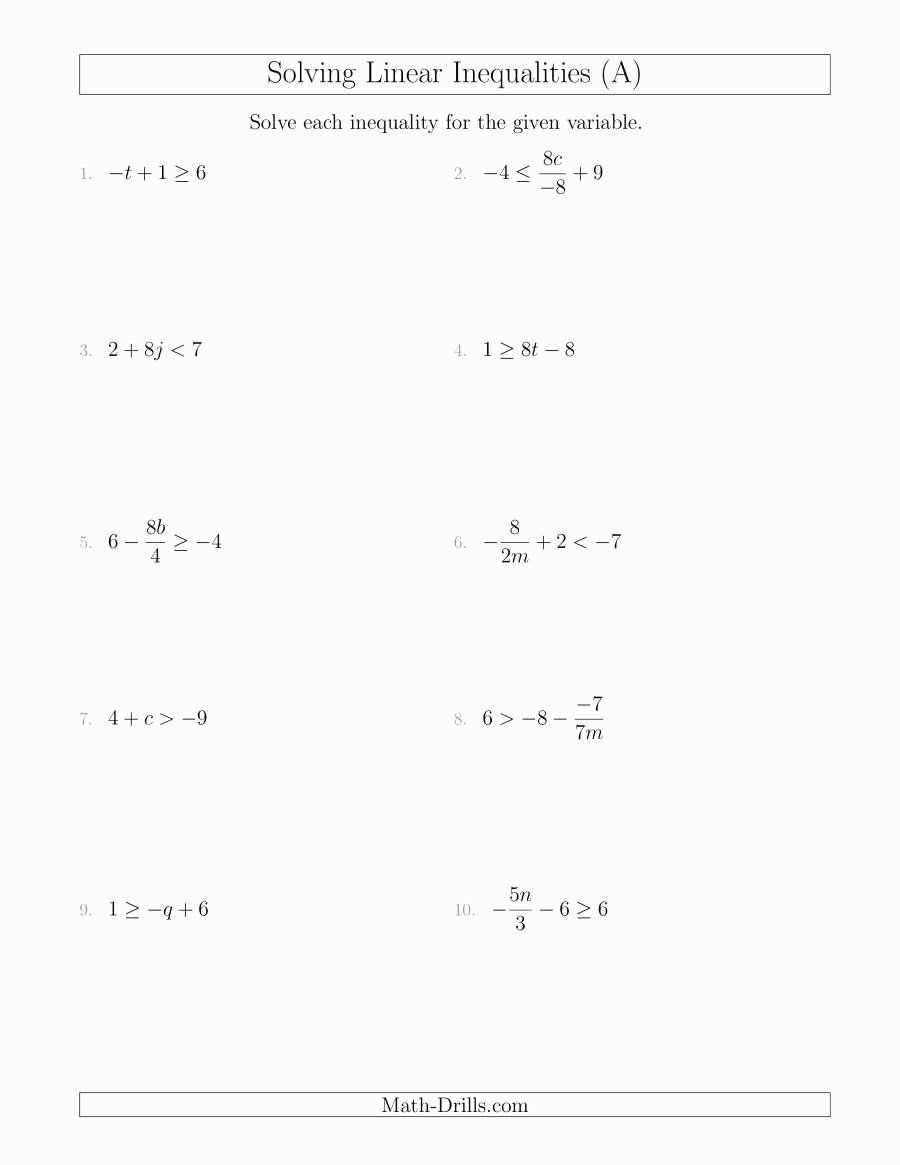
In the field of health and medicine, inequalities are used to analyze and predict health outcomes. For example, public health researchers use inequalities to study the relationship between social determinants of health (such as income, education, and access to healthcare) and health outcomes.
Inequalities are also used in medical research to determine the effectiveness of interventions or treatments. By comparing the outcomes of different groups of participants, researchers can identify if a treatment is more effective for certain individuals.
Conclusion
Inequalities are a powerful tool for modeling and solving problems in various fields. They allow us to analyze and make decisions based on quantities that are not equal, providing valuable insights into real-life situations. Whether it’s in finance, transportation, or health and medicine, inequalities play a crucial role in helping us navigate the complexities of the world around us.
So next time you encounter a problem that involves quantities that are not equal, remember to turn to inequalities for a solution!